Презентация на тему: Теорема Минковского о многогранниках

Теорема Минковского о многогранникахВыполниласт. гр. 4219-1Прожуган Яна

Теорема, о которой пойдет речь, наряду со знаменитыми теоремами Эйлера, Коши, Александрова, принадлежит к числу наиболее удивительных и глубоких результатов о многогранниках. ●Эта теорема была доказана в 1897 году выдающимся немецким математиком Германом Минковским (1864-1909).

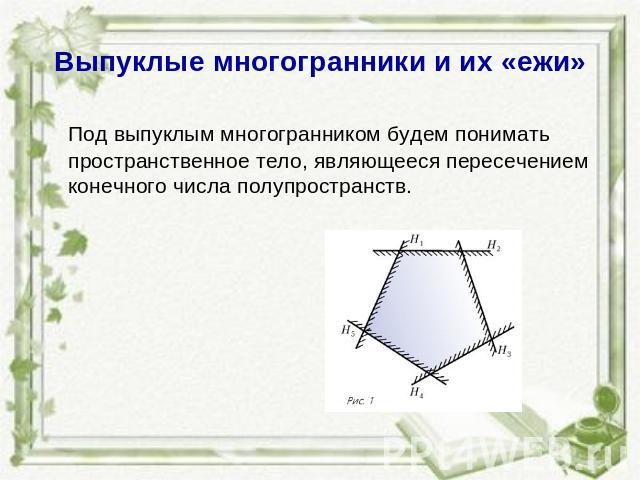
Выпуклые многогранники и их «ежи» Под выпуклым многогранником будем понимать пространственное тело, являющееся пересечением конечного числа полупространств.

Введем важное понятие опорной плоскости. Плоскость, имеющая с данным многоранником общие точки, но оставляющая многогранник по одну от себя сторону, называется опорной.

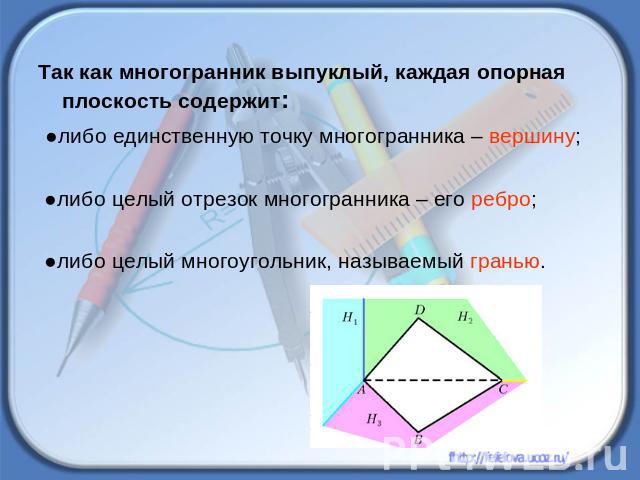
Так как многогранник выпуклый, каждая опорная плоскость содержит: ●либо единственную точку многогранника – вершину; ●либо целый отрезок многогранника – его ребро; ●либо целый многоугольник, называемый гранью.

Теорема Минковского Предположим, что дана система векторов в трехмерном пространстве с нулевой сумой. Является ли она ежом какого-нибудь многогранника? Удивительная теорема Минковского утверждает, что да, является.

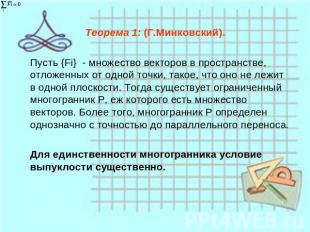
Теорема 1: (Г.Минковский). Пусть {Fi} - множество векторов в пространстве, отложенных от одной точки, такое, что оно не лежит в одной плоскости. Тогда существует ограниченный многогранник Р, еж которого есть множество векторов. Более того, многогранник Р определен однозначно с точностью до параллельного переноса. Для единственности многогранника условие выпуклости существенно.

Доказательство, данное Минковским, опирается на известный из Лагранжа. Другое доказательство было дано выдающимся росийским геометром А.Д. Александровым(1912-1999).

Теорема Минковского (точнее, ее аналог) верна для многогранников любой размерности. Для случая плоских многоугольников она доказывается несложно.

Центрально-симметричные многогранники Теорема Минковского чрезвычайно продуктивна. С ее помощью доказывается ряд теорем:Теорема 2: Если еж многогранника Р центрально- симметричен, то многогранник Р также центрально-симметричен.

Теорема 3: Выпуклый многогранник Р тогда и только тогда центрально-симметричен, когда у каждой грани имеется параллельная грань той же площади.Теорема 4: Если выпуклый многогранник Р составлен из конечного числа центрально-симметричных многогранников Р1, Р2,….,Рк, то и сам многогранник Р центрально-симметричен.

Многогранники с центрально-симметричными гранями Грани у центрально-симметричного многогранника не обязательно симметричны. Например, у октаэдра, который является центрально-симметричным многогранником, все грани – треугольники. Так что симметричность граней не является необходимым условием центрально-симметричного многогранника. Но является ли она достаточным условием? Оказывается да, является.

Теорема 5: (А.Д.Александров). Если все грани выпуклого многогранника Р центрально-симметричны, то и сам многогранник Р центрально-симметричный.Доказательство теоремы Александрова также опирается на теорему Минковского.