Презентация на тему: Понятие математической логики

ПОНЯТИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

Логика — наука о законах и правилах мышления.Формальная логика — наука о законах и формах мышления.Математическая логика изучает логические связи и отношения, лежащие в основе дедуктивного вывода.

В 4 века до н.э. древнегреческий ученый Аристотель заложил основы формальной логики. Он исследовал терминологию логики, разобрал теорию умозаключений и доказательств, вывел понятие силлогизма.В 16 веке в алгебре была создана буквенная символика. Она получила название алгебры логики, или математической логики. Основы математической логики заложил в 17 веке немецкий математик Лейбниц. Он сделал попытку построить первые логические исчисления. Лейбниц только развил идею, а окончательно развил и сформулировал ее ученый Джон Буль (1815-1864). В работах Буля логика приобрела свой алфавит, грамматику, орфографию. Поэтому иногда математическую логику называют Булевой алгеброй.

Алгебра логики — это математический аппарат, с помощью которого записывается, вычисляется, упрощается и преобразуется логическое высказывание.Основным понятием математической логики является высказывание.Высказывание — это повествовательное предложение, про которое всегда можно сказать истинное оно или ложное.Истинные высказывания обозначаются — 1, а ложные — 0Высказывания бывают просты и сложные. Сложные состоят из простых, соединенных знаками логических операций.Высказывания обозначаются заглавными буквами латинского алфавита (простые): A,B,C,D…

1.Инверсия•соответствует частице НЕ•обозначается ¬А•называется: отрицание

2.Конъюнкция•соответствует союзу И•обозначается &, ●•называется: логическое умножение

3.Дизъюнкция•соответствует союзу ИЛИ•обозначается v •называется: логическое сложение

ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений.
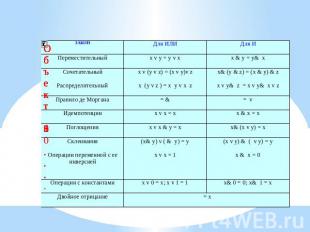

Равносильные преобразования логических формул имеют то же назначение что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определенному виду путем использования основных законов алгебры логики.Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного, сочетательного законов и т.д.), но есть и другие преобразования (использование распределительного закона для конъюнкции, законы поглощения, склеивания, де Моргана и др.)