Презентация на тему: Основы высшей математики и математической статистики

Основы высшей математики и математической статистики

Учебники: Н.Л. Лобоцкая и др. Высшая математика. Мн.1987г.Морозов Ю.В. Основы высшей математики и статистики. М. 1998г.И.В. Павлушков и соавт. Основы высшей математики и математической статистики. М.2004г.

Лекция 1 Предел функции.Производная функции.Дифференциал функции.

§2. Пределып.1. Предел функции Любой интервал (a,b), содержащий точку х0, называется окрестностью точки х0.Интервал (х0- δ, х0+ δ), где ε>0, симметричный относительно х0, называется δ -окрестностью точки х0.Пусть функция f(x) определена в некоторой окрестности точки х0, кроме, может быть, самой точки х0.Число A называется пределом функции f(x) в точке х0, если для любого числа ε>0 найдется такое положительное число δ, что для любого х≠ х0, удовлетворяющего неравенству |х- х0|< δ, выполняется соотношение |f(x)-A|< ε.ОБОЗНАЧЕНИЕ:

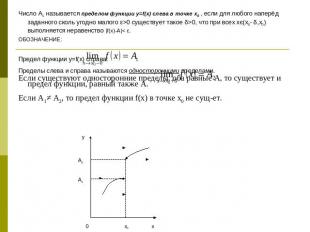
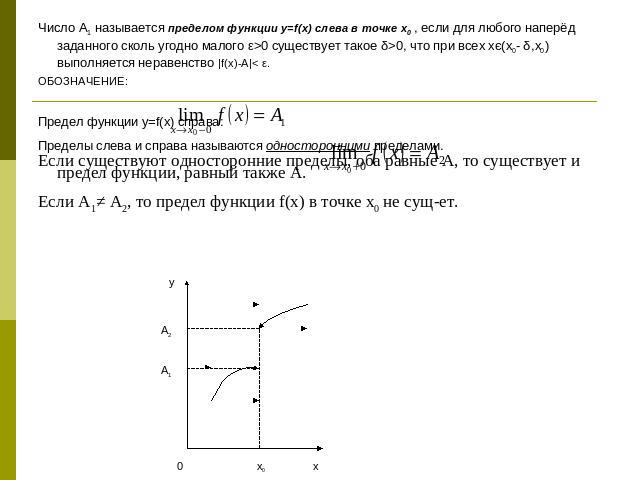
Число A1 называется пределом функции y=f(x) слева в точке х0 , если для любого наперёд заданного сколь угодно малого ε>0 существует такое δ>0, что при всех хє(х0- δ,х0) выполняется неравенство |f(x)-A|< ε.ОБОЗНАЧЕНИЕ: Предел функции y=f(x) справа: Пределы слева и справа называются односторонними пределами.Если существуют односторонние пределы, оба равные А, то существует и предел функции, равный также А.Если А1≠ А2, то предел функции f(x) в точке х0 не сущ-ет.

П.2. Бесконечно малые функции. Функция f(x) называется бесконечно малой при х->x0, если .Обозначение: α, β, γ и т.д.Если α(х) – бесконечно малая функция (величина), то - бесконечно большая величина, т.е. Свойства бесконечно малых.Теорема 1. Если функция f(x) имеет предел при х->x0, равный А, то она представима в виде f(x) = А + α(х) , где α(х) – б.м.ф.Справедливо и обратное: если функция f(x) представима равенством f(x) = А + α(х) при х->x0, то её предел равен А.Теорема 2. Алгебраическая сумма конечного числа бесконечно малых в точке функций есть бесконечно малая функция

Теорема 3. Произведение ограниченной при функции на бесконечно малую есть бесконечно малая функция.Следствие 1. Произведение постоянной величины на бесконечно малую есть функция бесконечно малая.Следствие 2. Произведение конечного числа бесконечно малых функций есть функция бесконечно малая

п.3. Непрерывные функции Функция f(x) называется непрерывной в точке x=x0, если Функция f(x) называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функцииФункция f(x) называется непрерывной в интервале, если она непрерывна в каждой точке этого интервала.Если функция f(x) в точке х0 не является непрерывной, то эта точка называется точкой разрыва, а функция разрывной в данной точке.

П.4. Основные теоремы о пределах Теорема 1.Предел алгебраической суммы конечного числа функций равен сумме пределов этих функций. , k - constСледствие.Предел постоянной равен самой постоянной , С – const.Теорема 2.Предел произведения конечного числа функций равен произведению пределов этих функций

Теорема 3.Предел частного двух функций равен частному пределов этих функций в случае, если предел знаменателя отличен от нуля.Теорема 4.Предел сложной, непрерывной функции определяется формулойТ.е. знак предела и функции можно менять местами

П.5. Методы вычисления пределов С помощью теорем о пределах и подстановкиРазложение на множителиУмножение на сопряженное выражение

Деление на наивысшую (наименьшую) степень аргументаС использованием замечательных пределов - основание натурального логарифма

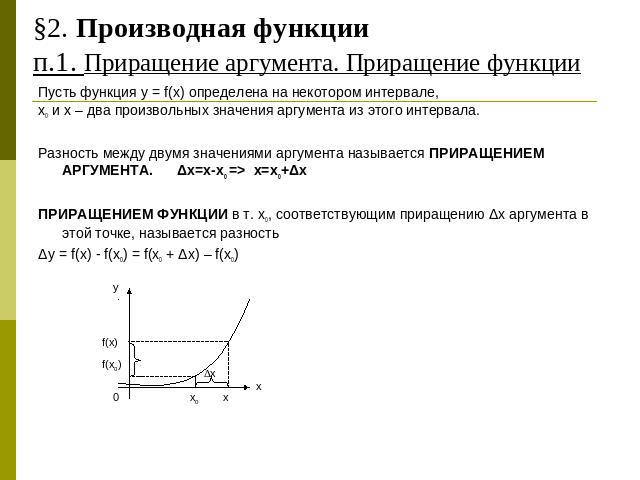
§2. Производная функциип.1. Приращение аргумента. Приращение функции Пусть функция y = f(x) определена на некотором интервале, х0 и x – два произвольных значения аргумента из этого интервала.Разность между двумя значениями аргумента называется ПРИРАЩЕНИЕМ АРГУМЕНТА. Δх=x-x0 => x=x0+ΔхПРИРАЩЕНИЕМ ФУНКЦИИ в т. x0, соответствующим приращению Δх аргумента в этой точке, называется разность Δy = f(x) - f(x0) = f(x0 + Δx) – f(x0)

Определение производной. Пусть дана функция f(x), определенная и непрерывная на интервале (а, b). Дадим аргументу хє(а, b) приращение Δх, такое что (x+ Δх)є(а, b).Тогда функция f(x) получит приращение Δf =f(x+ Δх)- f(x): Предел отношения приращения Δf функции f(x) к соответствующему приращению Δх аргумента х при стремлении Δх к нулю, называется ПРОИЗВОДНОЙ ФУНКЦИИ f(x) в точке х, при условии, что этот предел существует. ОБОЗНАЧЕНИЕ:Функция, для которой в точке х существует конечная производная называется дифференцируемой в данной точке.Если функция имеет конечные производные во всех точках некоторого промежутка, то она называется дифференцируемой на данном промежутке.

Физический смысл первой производной функции.мгновенная скорость протекания физических, химических и др. процессов находится как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. (физический смысл производной)Геометрический смысл первой производной.Угловой коэффициент касательной, проведенной к графику дифференцируемой функции в некоторой точке, численно равен производной функции в данной точке.(угл. коэф. касательной = тангенс угла наклона касательной) Уравнение касательной к функции y=f(x) в точке (x0,y0) имеет вид: , где y0=f(x0)

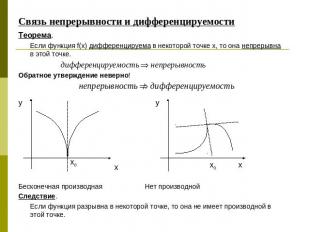
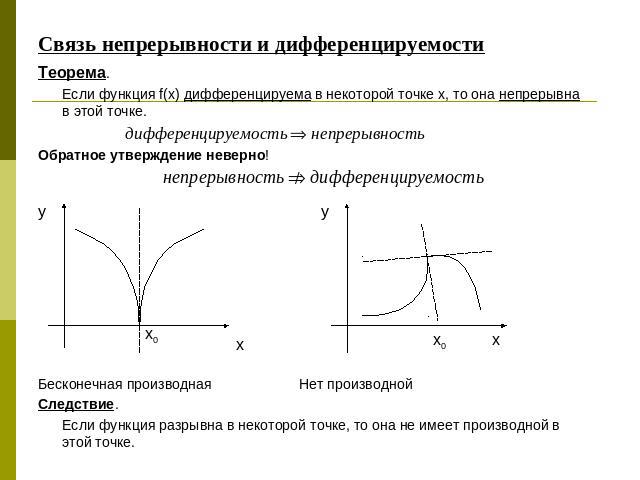
Связь непрерывности и дифференцируемости Теорема.Если функция f(x) дифференцируема в некоторой точке х, то она непрерывна в этой точке.Обратное утверждение неверно!Бесконечная производная Нет производнойСледствие.Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

Правила дифференцирования.Производная постоянной величины равна нулю.Производная алгебраической суммы конечного числа функций равна сумме производных слагаемыхПроизводная произведения двух функций определяется формулойПроизводная частного от деления двух функций определяется формулой

Производная сложной функцииТеорема.Если функция u=g(x) имеет производную u’x=g’(x) в точке x, а функция y=f(u) – производную y’u=f’(u) в соответствующей точке u, то сложная функция y=f(g(x)) в данной точке х имеет производную y’x=F’(x), которая находится по формулеНахождение производной идет в порядке, противоположном порядку вычисления функции.Пример. Вычислить производную функцииРешение. Нахождение y’:Т.о.

§2. Дифференциал функцииСогласно определению производнойНа основании теоремы о представлении функции как суммы её предела и б.м.ф., данное равенство означает, что где α(Δх) – б.м. при Δх→0 Первое слагаемое стремится к нулю при Δx->0 медленнее второго, поэтому его называют главной частью приращения функции.Главная часть приращения функции Δy, равная произведению y’ Δx, называется дифференциалом первого порядка от функции y=f(x), соответствующим выбранным значениям x и Δx. (аналитический смысл дифференциала)Обозначение: dy = f’(x)Δх

Механический смысл дифференциала Если s=f(t) есть путь, пройденный материальной точкой за время t, то производная s’t есть скорость движения в момент времени t.Тогда дифференциал пути ds =f’(t)Δt приближенно равен пути, пройденному материальной точкой от момента времени t до момента времени t+Δt, если пренебречь изменением скорости движения на данном промежутке времени. Вторая форма записи дифференциалаdx = Δх, т.к. у = х => dy = dx = x’· Δх = Δх Тогда dy = f’(x) · dx - другое обозначение производной

Свойства дифференциала 1. 2. 3. , k- const Дифференциал сложной функцииЕсли y = f(u), u = g(x) – дифференцируемые функции своих аргументов, то производная функция y = f(g(x)) выражается формулой Пример. Вычислить дифференциал функцииРешение.

Производные высших порядков. Производную f’(x) функции y = f(x) называется ПРОИЗВОДНОЙ ПЕРВОГО ПОРЯДКА или просто первой производной этой функции.Производная функции является функцией => ее можно дифференцировать.ВТОРОЙ ПРОИЗВОДНОЙ ФУНКЦИИ или производной второго порядка называется производная от ее первой производной. Производная (n-1)й производной (nєN) называется ПРОИЗВОДНОЙ n-го ПОРЯДКА или n-й производной.Обозначение: f(n)(x)

Физический смысл второй производной Вторая производная функции есть мгновенное ускорение амгн прямолинейно движущейся точки в момент времени t

Спасибо за внимание.До свидания!