Презентация на тему: Тела вращения на примере конуса

Компьютерная поддержка по теме"Тела вращения на примере конуса"Презентацию подготовила ученица 9 класса Виноградова Наталья

Историческая справка о конусеКонус в переводе с греческого «konos» означает «сосновая шишка». С конусом люди знакомы с глубокой древности. Много сделала для геометрии школа Платона (428–348 гг. до н. э.). Школе Платона, в частности, принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.

Историческая справка о конусеБольшой трактат о конических сечениях был написан Аполлонием Пергским– учеником Евклида, который создал великий труд из 15 книг под названием «Начала». Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.

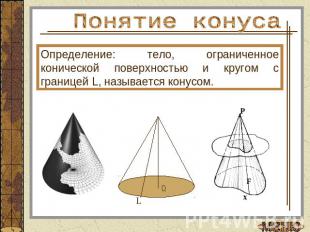
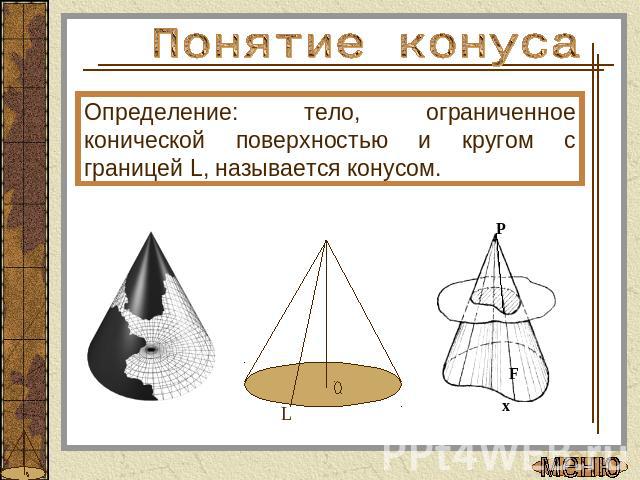
Понятие конусаОпределение: тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.

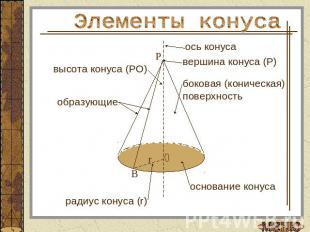
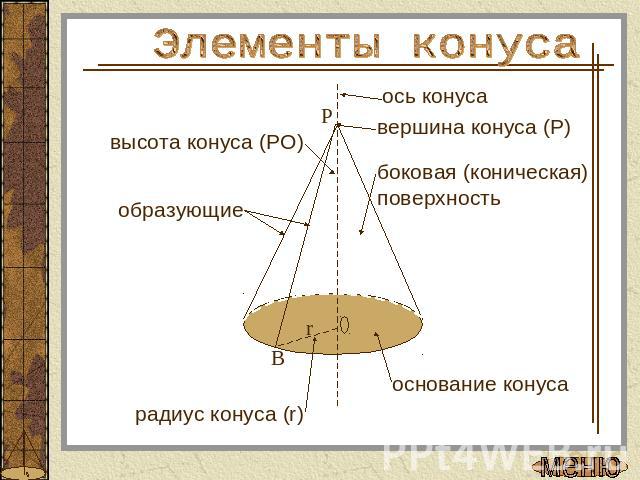
Элементы конуса

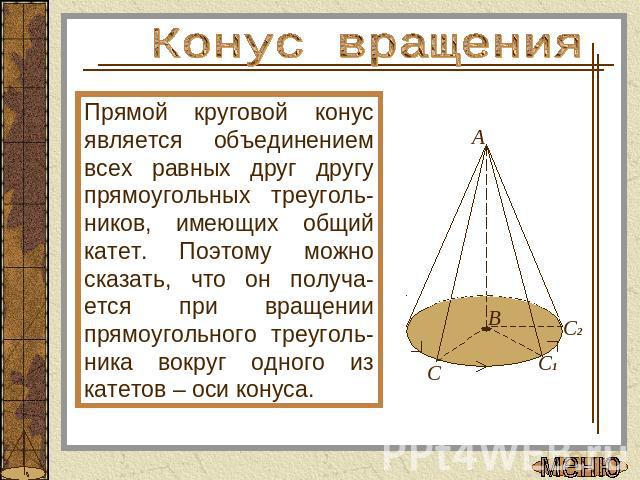
Конус вращенияПрямой круговой конус является объединением всех равных друг другу прямоугольных треуголь-ников, имеющих общий катет. Поэтому можно сказать, что он получа-ется при вращении прямоугольного треуголь-ника вокруг одного из катетов – оси конуса.

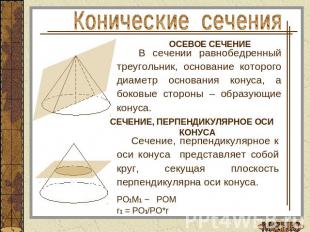
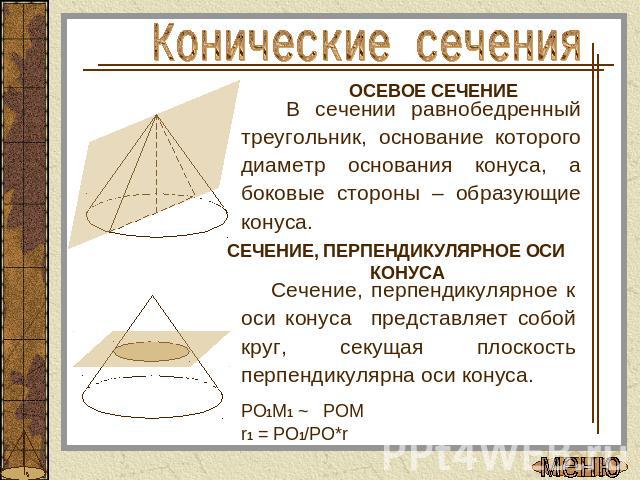
Конические сечения В сечении равнобедренный треугольник, основание которого диаметр основания конуса, а боковые стороны – образующие конуса.СЕЧЕНИЕ, ПЕРПЕНДИКУЛЯРНОЕ ОСИ КОНУСА Сечение, перпендикулярное к оси конуса представляет собой круг, секущая плоскость перпендикулярна оси конуса.РО1М1 ~ РОМr1 = РО1/РО*r

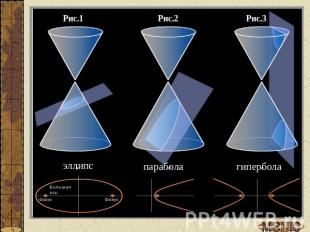
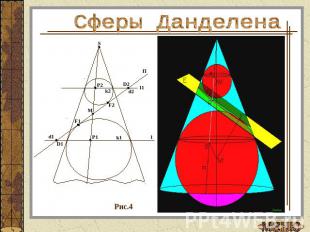
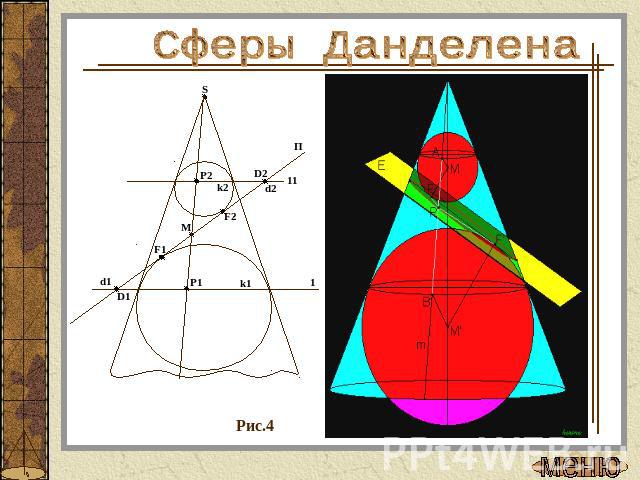
Сферы Данделена

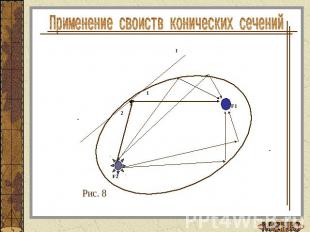
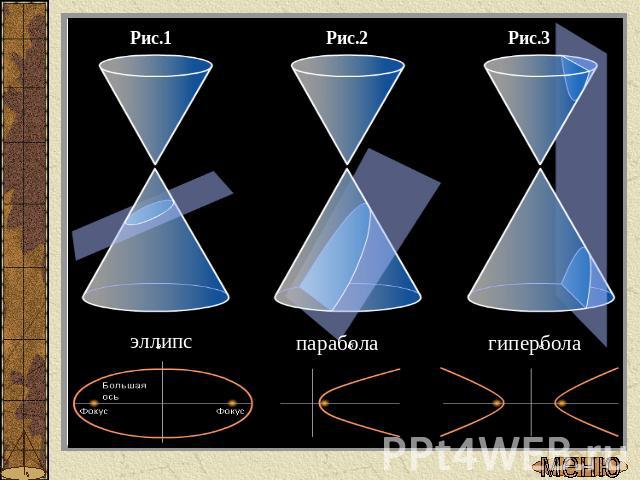
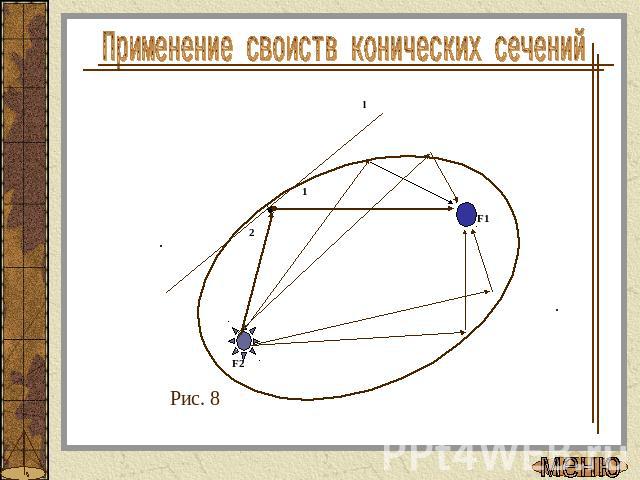
Применение своиств конических сечений

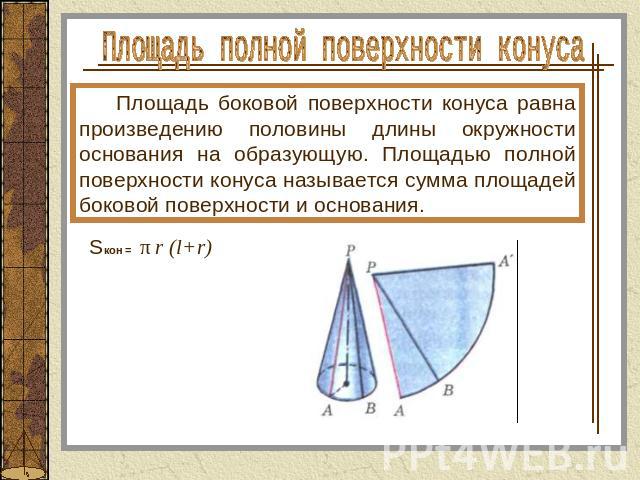
Площадь боковой поверхности конуса За площадь боковой поверхности конуса принимается площадь его развертки (конической поверхности).

Площадь полной поверхности конуса Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую. Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания.

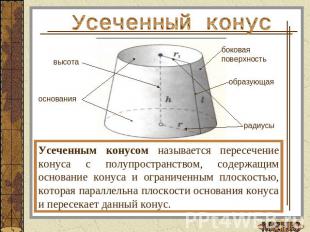
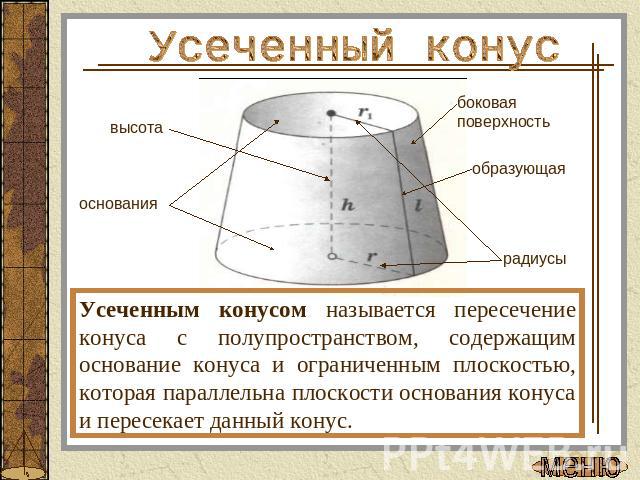
Усеченный конусУсеченным конусом называется пересечение конуса с полупространством, содержащим основание конуса и ограниченным плоскостью, которая параллельна плоскости основания конуса и пересекает данный конус.

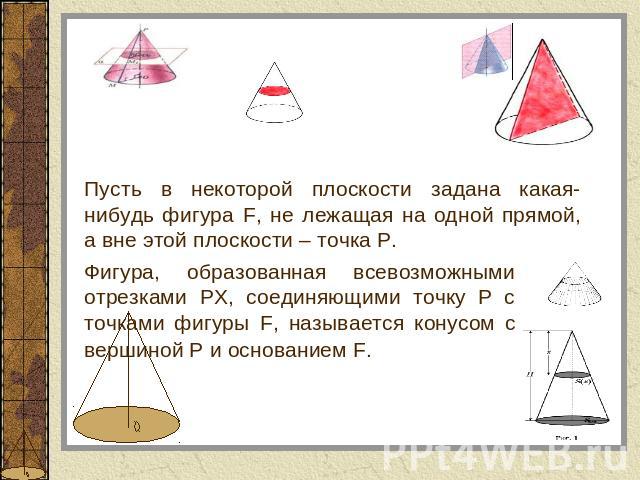
Пусть в некоторой плоскости задана какая-нибудь фигура F, не лежащая на одной прямой, а вне этой плоскости – точка P. Фигура, образованная всевозможными отрезками PX, соединяющими точку P с точками фигуры F, называется конусом с вершиной Р и основанием F.

Используемые ресурсы http://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BD%D1%83%D1%81http://images.yandex.ru/yandsearch?p=0&text=%D0%BA%D0%BE%D0%BD%D1%83%D1%81&img_url=900igr.net%2Fdatai%2Fgeometrija%2FObjom-konusa%2F0001-001-Obem-konusa.jpg&rpt=simage&noreask=1&lr=2