Презентация на тему: Законы и правила математической логики

Законы и правила математической логики Упрощение сложных высказываний

Основные законы алгебры логики

Основные законы алгебры логики

МОРГАН Огастес де (Morgan Augustus de) Морган Огастес (Августус) де (27.6.1806-18.3. 1871)-шотландский математик и логик. Секретарь Королевcкого астрономического общества (1847г.), член Лондонского королевского общества. Первый президент Лондонского математического общества. Родился в Мадуре (Индия). Учился в Тринити-колледж (в Кембридже). Профессор математики в университетском колледже в Лондоне. Основные труды по алгебре, математическому анализу и математической логике. В теории рядов описал логарифмическую шкалу для критериев сходимости; занимался теорией расходящихся рядов. Один из основателей формальной алгебры. Продолжая работы Дж. Пикока, Морган в 1841-1847гг. опубликовал ряд работ по основам алгебры. В трактате "Формальная логика или исчисление выводов необходимых и возможных" (1847г.), Морган некоторыми своими положениями опередил Дж. Буля. Позднее Морган успешно изучал логику отношений - область, не охваченную исследованиями предшественников. В книге "Тригонометрия и двойная алгебра" (1849г.) развил мысль У. Гамильтона о распространении идей символической алгебры на исчисление комплексных величин. Благодаря этому комплексные величины были строго обоснованы не только геометрически, но и алгебраически. Написал много исторических работ, в частности книгу "Бюджет парадоксов" (1872г.). Большой вклад внес также в дедуктивную логику вообще и математическую в частности. Лондонское математическое общество учредило медаль им. О. Моргана.

Задание 1. Упростить выражение: _ X ∙ Y V X ∙ Y Воспользуемся распределительным законом: Х ∙ ( Y V Z ) = X ∙ Y V X ∙ Z (или вынесем общий множитель за скобку)

Задание 2. Упростите логическое выражение _______________ _____ F= (A v B)→ (B v C). Избавимся от импликации и отрицания. Воспользуемся (¬(A→B)=A& ¬ B). Получится: ¬((AvB)→ ¬(BvC))= (AvB)& ¬ (¬(BvC)). Применим закон двойного отрицания, получим:(A v В) & ¬(¬(В v С)) = (A v В) & (B v С). Применим правило дистрибутивности ((A∙B) +(A∙C) = A∙(B+C)). Получим: (AvВ)& (B v С)= (AvB)&Bv(AvB)&C Применим закон коммутативности (A&B=B&A ) и дистрибутивности (16). Получим: (AvB)&Bv(AvB)&C = A&BvB&BvA&CvB&C. Применим (А& A= A) и получим: A&BvB&BvA&CvB&C= A&BvBvA&CvB&C Применим ((A&B) v(A&C) = A&(BvC) ), т.е. вынесем за скобки В.Получим:A&BvBvA&CvB&C= B& (Av1)vA&CvB&C. Применим (Аv 1= 1 ). Получим:B& (Av1) vA&CvB&C= BvA&CvB&C. Переставим местами слагаемые, сгруппируем и вынесем В за скобки. Получим:BvA&CvB&C = B& (1vC)vA&C. Применим (Аv 1= 1 ) и получим ответ: B&(1vC)vA&C=BvA&C.

IV. Закрепление изученного №1 Упростите выражение: F = ¬ (A&B) v ¬ (BvC). F = (A→B) v (B→A). F = A&CvĀ&C. F =AvBvCvAvBvC Ответы: F = ¬ (A&B) v ¬ (BvC) =AvB. F= (A→B) v (B→A) = 1. F = A&CvĀ&C=C. F =AvBvCvAvBvC=1.

№2 Упростите выражение: F = ¬(X&Yv ¬(X&Y)). F = X&¬ (YvX). F = (XvZ) & (XvZ) & (YvZ). Ответы: F = ¬(X&Yv ¬(X&Y)) = 0. F = X&¬ (YvX) = X&Y. F = (XvZ) & (XvZ) & (YvZ) =X&(YvZ).

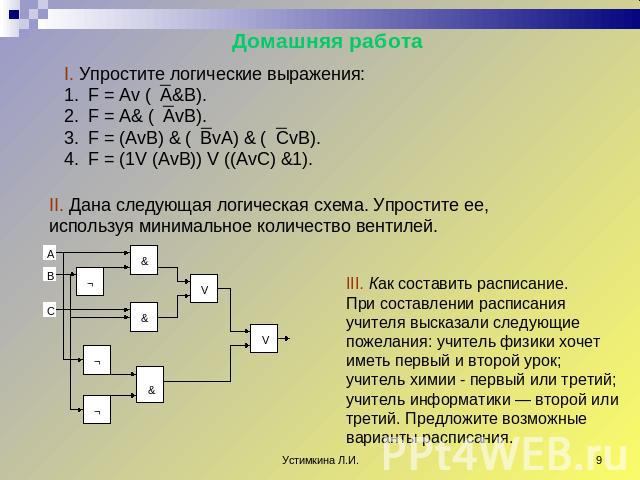
Домашняя работа I. Упростите логические выражения: F = Av (A&B). F = A& (AvB). F = (AvB) & (BvA) & (CvB). F = (1V (AvB)) V ((AvC) &1). II. Дана следующая логическая схема. Упростите ее, используя минимальное количество вентилей. III. Как составить расписание. При составлении расписания учителя высказали следующие пожелания: учитель физики хочет иметь первый и второй урок; учитель химии - первый или третий; учитель информатики — второй или третий. Предложите возможные варианты расписания.