Презентация на тему: Понятие бесконечной интегральной суммы. Интеграл

Алгебра и начала анализа, 11 класс Понятие бесконечной интегральной суммы. Интеграл. – формула Ньютона-Лейбница

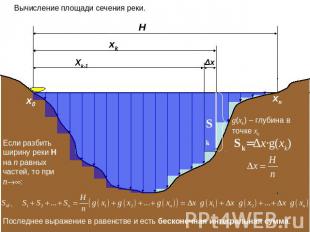
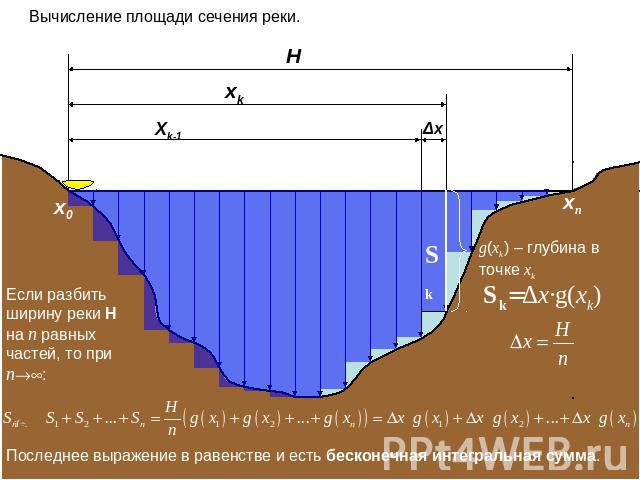
Если разбить ширину реки H на n равных частей, то при n: Вычисление площади сечения реки. g(xk) – глубина в точке xk Последнее выражение в равенстве и есть бесконечная интегральная сумма.

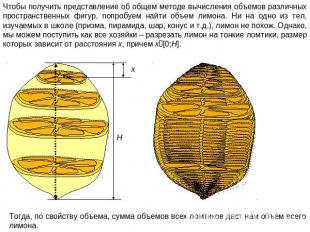
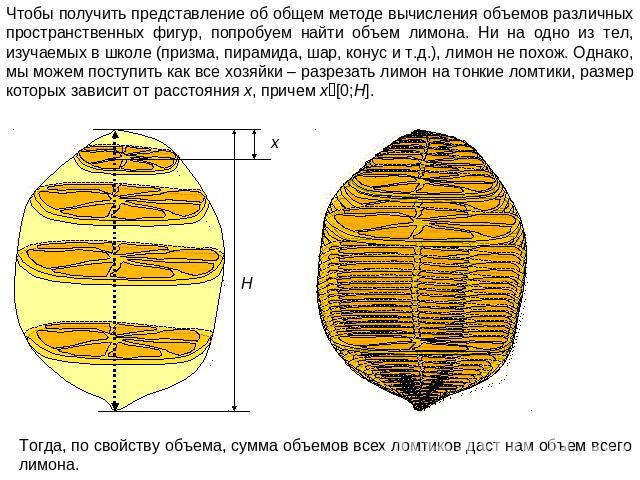
Чтобы получить представление об общем методе вычисления объемов различных пространственных фигур, попробуем найти объем лимона. Ни на одно из тел, изучаемых в школе (призма, пирамида, шар, конус и т.д.), лимон не похож. Однако, мы можем поступить как все хозяйки – разрезать лимон на тонкие ломтики, размер которых зависит от расстояния x, причем x[0;H]. Тогда, по свойству объема, сумма объемов всех ломтиков даст нам объем всего лимона.

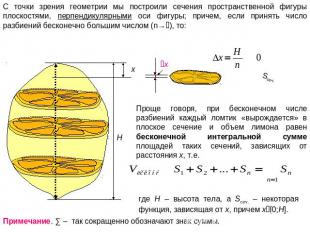
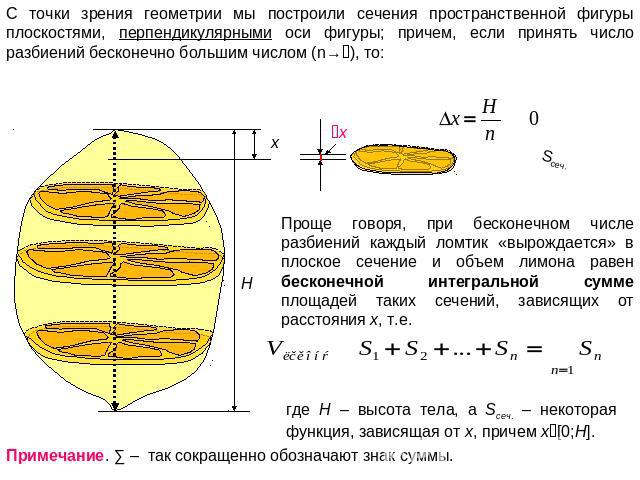
С точки зрения геометрии мы построили сечения пространственной фигуры плоскостями, перпендикулярными оси фигуры; причем, если принять число разбиений бесконечно большим числом (n→), то: Проще говоря, при бесконечном числе разбиений каждый ломтик «вырождается» в плоское сечение и объем лимона равен бесконечной интегральной сумме площадей таких сечений, зависящих от расстояния x, т.е. где H – высота тела, а Sсеч. – некоторая функция, зависящая от x, причем x[0;H]. Примечание. ∑ – так сокращенно обозначают знак суммы.

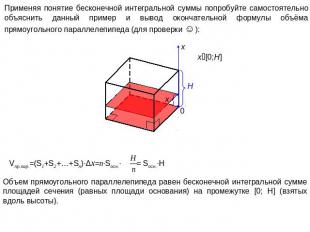
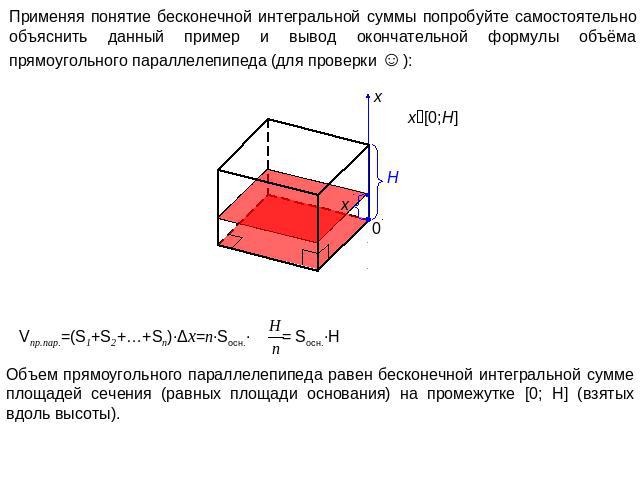
Применяя понятие бесконечной интегральной суммы попробуйте самостоятельно объяснить данный пример и вывод окончательной формулы объёма прямоугольного параллелепипеда (для проверки ☺): Vпр.пар.=(S1+S2+…+Sn)∙Δx=n∙Sосн.∙ = Sосн.∙H Объем прямоугольного параллелепипеда равен бесконечной интегральной сумме площадей сечения (равных площади основания) на промежутке [0; H] (взятых вдоль высоты).

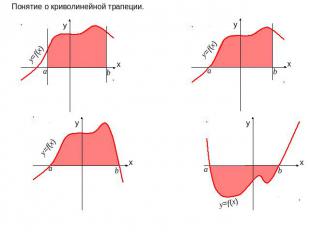
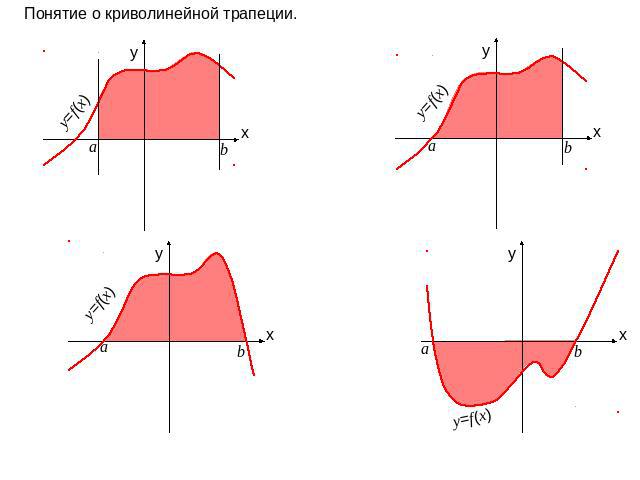
Понятие о криволинейной трапеции.

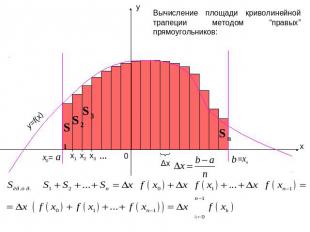
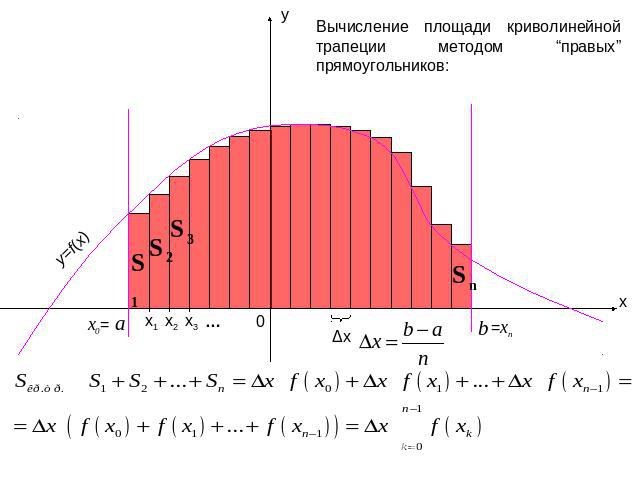
Вычисление площади криволинейной трапеции методом “правых” прямоугольников:

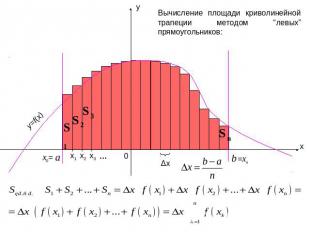
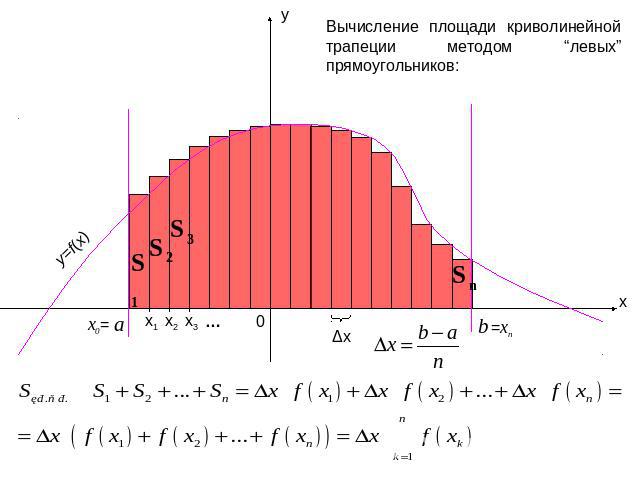
Вычисление площади криволинейной трапеции методом “левых” прямоугольников:

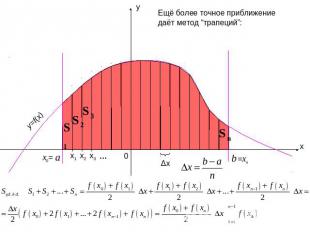
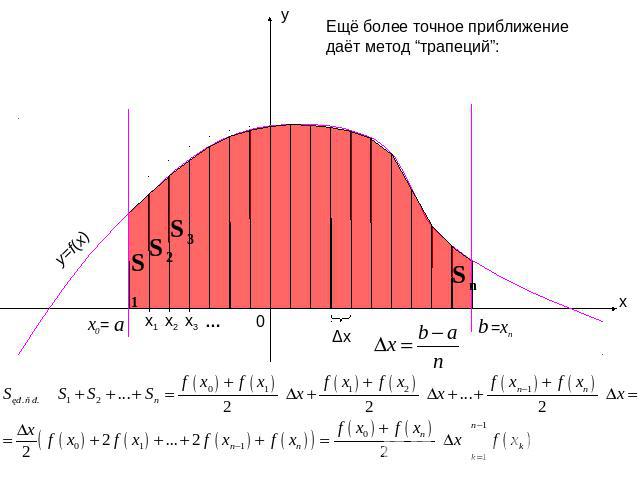
Ещё более точное приближение даёт метод “трапеций”:

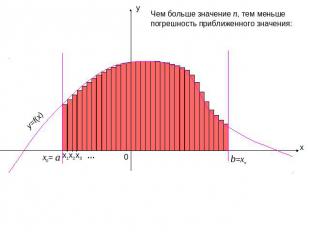
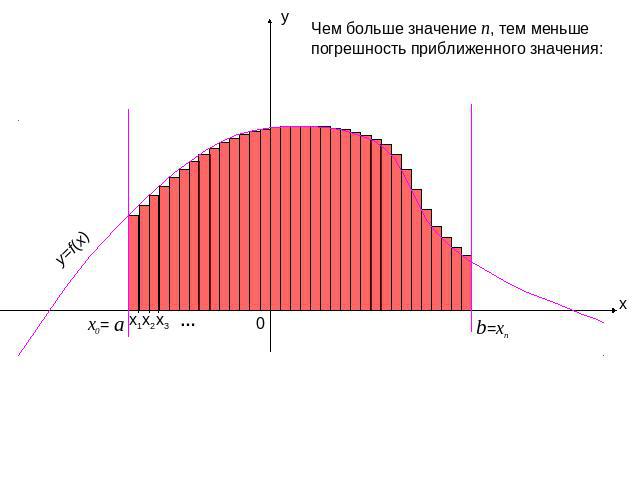
Чем больше значение n, тем меньше погрешность приближенного значения:

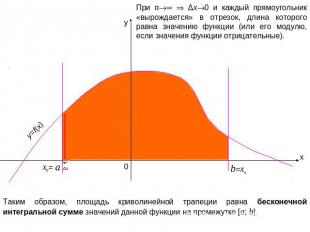
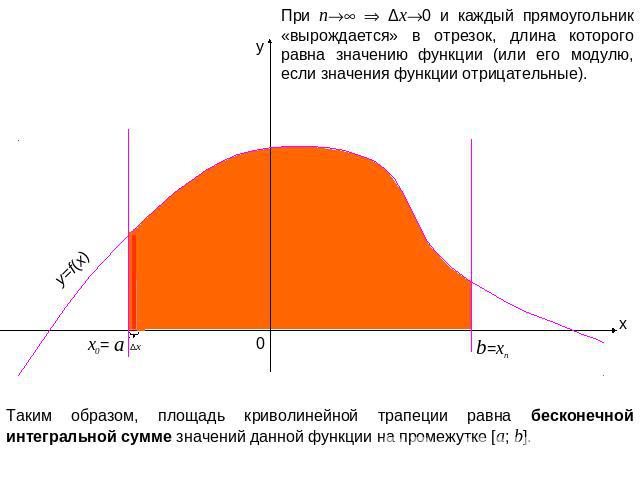
При n Δx0 и каждый прямоугольник «вырождается» в отрезок, длина которого равна значению функции (или его модулю, если значения функции отрицательные). Таким образом, площадь криволинейной трапеции равна бесконечной интегральной сумме значений данной функции на промежутке [a; b].

В приведенном выше примере мы находили площадь криволинейной трапеции с помощью понятия бесконечной интегральной суммы значений данной функции f(x) на отрезке [a; b]. В математике принята более короткая запись этого понятия – интеграл (∫), т.е. Читают: интеграл от a до b эф от икс дэ икс. Число a называют нижним пределом интегрирования, b – верхним пределом интегрирования, f(x) – подынтегральной функцией, x – переменной интегрирования. Примечание. Обратите внимание, что знак интеграла напоминает стилизованную букву S, что естественно из геометрического смысла этого понятия. Если Вы владеете понятием предела (lim), то можно дать следующее определение интеграла:

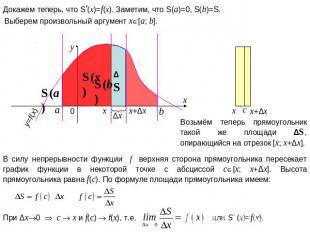
Докажем теперь, что S'(x)=f(x). Заметим, что S(a)=0, S(b)=S. Выберем произвольный аргумент x[a; b]. Возьмём теперь прямоугольник такой же площади ΔS, опирающийся на отрезок [x; x+Δx]. В силу непрерывности функции f верхняя сторона прямоугольника пересекает график функции в некоторой точке с абсциссой c[x; x+Δx]. Высота прямоугольника равна f(c). По формуле площади прямоугольника имеем:

Вы уже знакомы с понятием первообрáзной функции. Доказанное нами утверждение S'(x)=f(x) в силу основного свойства первообразных для всех x[a;b] означает, что: S(x)=F(x)+C, где С – некоторая постоянная, а F – одна из первообразных для функции f(x). Для нахождения С подставим x=a: F(a)+C=S(a)=0 F(a)=–C. Следовательно, S(x)=F(x) –F(a). Поскольку площадь криволинейной трапеции равна S(b)=S, подставляя x=b, получим: S = S(b) = F(b) – F(a)= Важно!!! понимать, что значение интеграла может получиться отрицательным (если, например, на заданном промежутке значения функции отрицательны).

Отметим некоторые свойства интеграла (объясните их с помощью учителя): Применение этих свойств часто упрощает вычисление интегралов.

Пример 3. Найти значение интеграла: . Решение.