Презентация на тему: Интеграл

Урок по алгебре и начала анализав 11классе Интеграл Учитель Стрельникова Любовь Петровна

«Путешествие в мир интегралов и первообразных»

Путешествие в мир интегралов и первообразных. Достижения крупные людямНикогда не давались легко!

Цели и задачи: Обучающие: обобщение и систематизация знаний учащихся; закрепление основных понятий базового уровня. Развивающие: развитие познавательного интереса; развитие логического мышления и внимания; формирование потребности в приобретении знаний. Воспитательные: воспитание сознательной дисциплины и норм поведения; воспитание ответственности, умения принимать самостоятельные решения.

Верно ли утверждение, определение, свойство? 1. Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка F‘(х)=f(х) 2. Если F‘(х)=0 на некотором промежутке I, то функция F не всегда постоянна на этом промежутке. 3. Пусть на отрезке [а; в] оси Ох задана непрерывная функция f, не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [а; в] и прямыми х=а и х=в называют криволинейной трапецией 4.Для любой непрерывной на отрезке [а;в] функции f Sn при n -> ∞ стремится к некоторому числу. Это число называют (по определению) интегралом функции f от а до в и обозначают 5.Официальной датой рождения дифференциального исчисления можно считать май 1684, когда Лейбниц опубликовал первую статью «Новый метод максимумов и минимумов…». Эта статья в сжатой и малодоступной форме излагала принципы нового метода, названного дифференциальным исчислением.

Устная работа. Существует ли интегралы: Назовите одну из первообразных для каждой из следующих функций:


Немного истории -1675 г, опубликовано в 1686 г ввел Г.Лейбниц - 1675 г, Ж Лагранж Официальной датой рождения дифференциального исчисления можно считать май 1684, когда Лейбниц опубликовал первую статью «Новый метод максимумов и минимумов…» В XIX веке Коши первым дал анализу твёрдое логическое обоснование, введя понятие предела последовательности, он же открыл новую страницу комплексного анализа. Пуассон, Лиувилль, Фурье и другие изучали дифференциальные уравнения в частных производных и гармонический анализ.

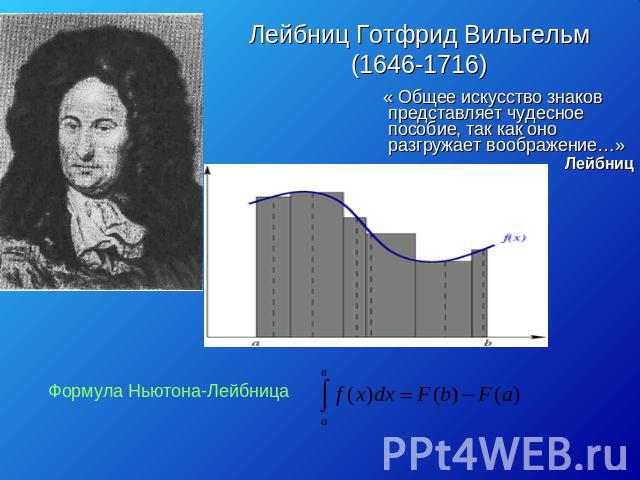
Лейбниц Готфрид Вильгельм (1646-1716) « Общее искусство знаков представляет чудесное пособие, так как оно разгружает воображение…» Лейбниц

Исаак Ньютон(1643-1727) Разумом он превосходил род человеческий. Лукреций

Немного истории «Интеграл» придумал Я.Бернулли (1690) «восстанавливать» от латинского integro «целый» от латинского integer

интегральное исчисление неопределенный интеграл (первообразная) И.Ньютон определенный интеграл (площадь криволинейной фигуры) Г.Лейбниц

Дифференцирование Интеграл функции — естественный аналог суммы последовательности. Согласно основной теореме анализа, интегрирование — операция, обратная к дифференцированию. Процесс нахождения интеграла называется интегрированием.
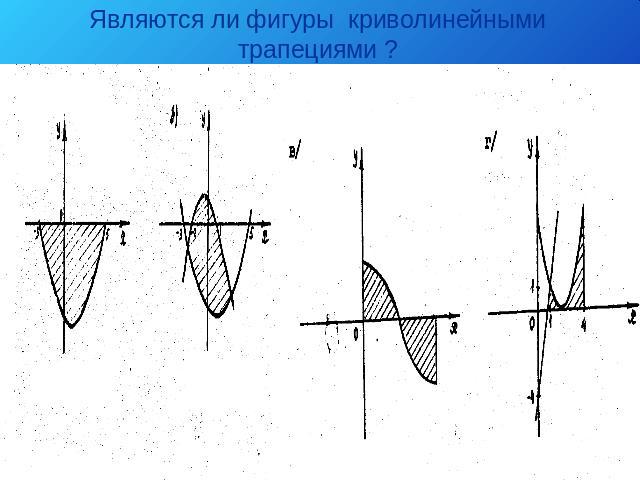
Являются ли фигуры криволинейными трапециями ?

Применение интеграла Площадь фигуры Объем тела вращения Работа электрического заряда Работа переменной силы Центр масс

Спасибо за урок!