Презентация на тему: Интеграл

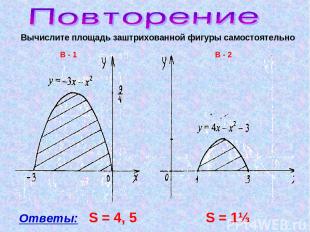
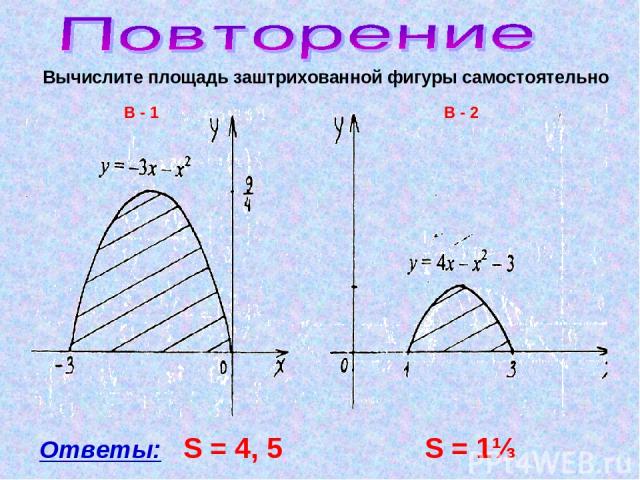
Вычислите площадь заштрихованной фигуры самостоятельно Ответы: S = 4, 5 S = 1⅓ В - 1 В - 2

Отрезок [а;в] разбит на n отрезков одинаковой длины точками х1;х2;… ;хn-1 ;хn. ∆х =(в – а)/n На каждом отрезке как на основании построим прямоугольник высотой f (xk-1). S = f (x k-1) ∆х = (в – а)/n f (x k-1). S n - сумма площадей всех прямоугольников В силу непрерывности f объединение построенных прямоугольников при большом n «почти совпадает» с криволинейной трапецией. Sn -> S при n -> ∞.

Для любой непрерывной на отрезке [ а; в ] функции f ( не обязательно неотрицательной ) Sn при n -> ∞ стремится к некоторому числу. Это число называется интегралом функции от а до в.

f ( x ) dx Т.е. Sn -> f ( x ) dx при n -> ∞ а и в – пределы интегрирования: в – верхний предел; а – нижний предел. Знак - знак интеграла. Функция f – подынтегральная функция. Переменная х – переменная интегрирования.

Г.В.Лейбниц Якоб Бернулли Иоганн Бернулли Символ интеграла введён Лейбницем (1675г.). Этот знак является изменением латинской буквы S ( первой буквы слова summa). Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integro, которое переводится как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования «восстанавливает» функцию, дифференцированием которой получена подынтегральная функция.) Возможно, происхождение слова интеграл иное: слово integer означает целый. В ходе переписки И. Бернулли и Г.Лейбниц согласились с предложением Я.Бернулли. Тогда же, в 1696г., появилось и название новой ветви математики – интегральное исчисление (calculus integralis), которое ввел И. Бернулли.

Сравнивая формулы для площади криволинейной трапеции S = F ( b ) – F ( a ) и S = f ( x ) dx Получаем Если F – первообразная для f на [а; в], то f ( x ) dx = F ( b ) – F ( a ) Формула верна для любой функции f, непрерывной на [а; в]

1. 1 / х2 dx – по определению не существует, т.к. на [ -1; 2 ] функция f ( х ) = 1 / х2 не является непрерывной, а значит функция F ( x ) = -1 / x не является первообразной для f ( х ) на [ -1; 2 ]. ( 0 Є [ -1; 2 ] не входит в D ( f )). 2. При а ≥ в При таком соглашении формула Ньютона – Лейбница оказывается верной при произвольных а и в. В частности,

Сформулируйте и докажите 1)

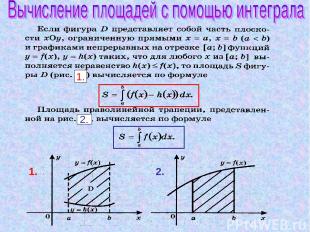
1. 2. 2. 1.

1. Вычислить интеграл от 0 до 2 функции f ( х ) = х 3 ( от – 1 до 1 ) 2. Вычислить интеграл от - π/4 до π функции f ( х ) = 3 cos 2х. 3. Вычислить площадь фигуры, ограниченной линиями f1 ( х ) = х2 ; f2 ( х ) = 2х 4. Вычислить площадь фигуры, ограниченной линиями: х = 0; у = х2 – 4х + 5 и касательной к этому графику в точке х0 = 2.

Найдите площадь фигуры ограниченной линиями у = х2 – 6х + 5 и у = 5 – 2х – х2 двумя способами: 1) с помощью площадей криволинейных трапеций; 2) с помощью интеграла и его свойств.

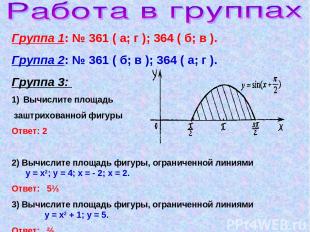
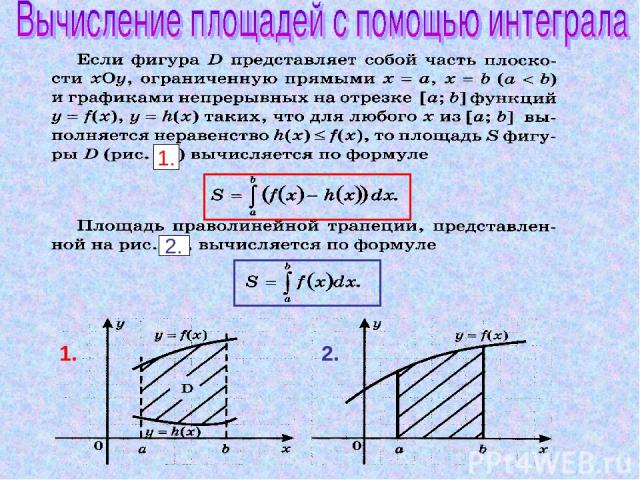
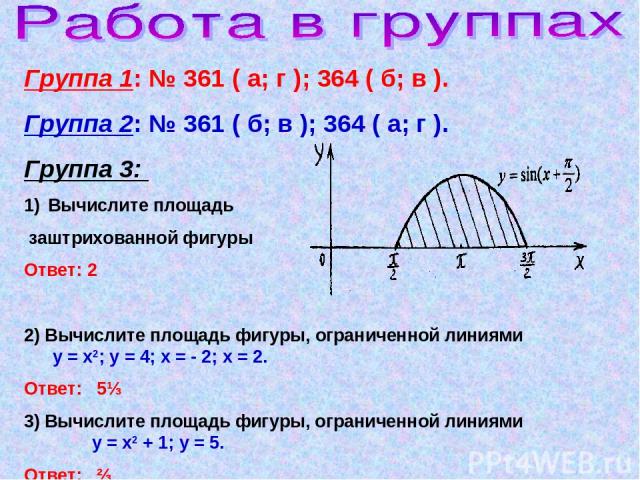
Группа 1: № 361 ( а; г ); 364 ( б; в ). Группа 2: № 361 ( б; в ); 364 ( а; г ). Группа 3: Вычислите площадь заштрихованной фигуры Ответ: 2 2) Вычислите площадь фигуры, ограниченной линиями у = х2; у = 4; х = - 2; х = 2. Ответ: 5⅓ 3) Вычислите площадь фигуры, ограниченной линиями у = х2 + 1; у = 5. Ответ: ⅔

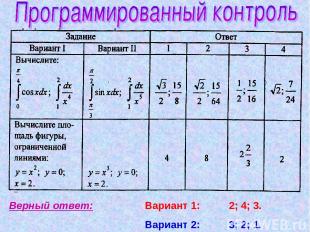
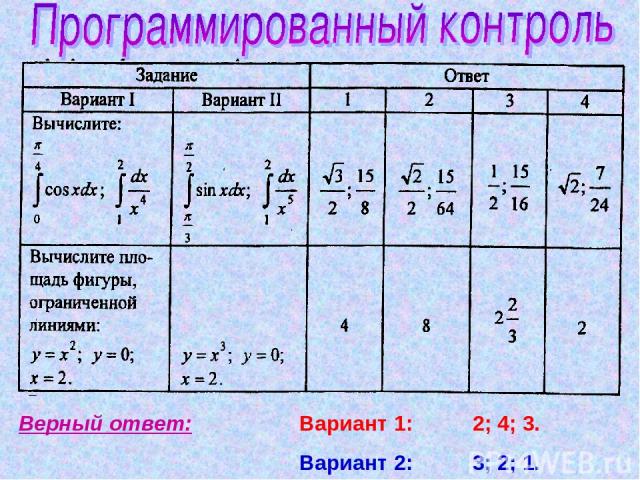
Верный ответ: Вариант 1: 2; 4; 3. Вариант 2: 3; 2; 1.

п. 30 ( выучить к зачёту по § 7 – 8 теоретический материал); № 362; 360 (а; г); повторить уравнение касательной п. 19. По желанию. Вычислите площадь фигуры, ограниченной линиями х = 0; у = sin х; у = cos х; х = π / 2. Ответ: 2 √ 2 – 2.