Презентация на тему: Аксиомы геометрии

Аксиомы геометрии

Евклид и его труды III в до н.э.

Такой подход, когда сначала формируются исходные положения-аксиомы, а затем на их основе путем логических рассуждений доказываются другие утверждения, зародился еще в глубокой древности и был изложен в знаменитом сочинении «Начала» древнегреческого ученого Евклида и сейчас используются в курсах геометрии, а сама геометрия, изложенная в «Началах», называется евклидовой геометрии.

Николай Иванович Лобачевский начало XIX в.

С современной точки зрения можно дать, например, следующее определение Л. г. на плоскости: она есть не что иное, как геометрия внутри круга на обычной (евклидовой) плоскости, лишь выраженная особым образом. Именно, рассматривают круг на обычной плоскости (рис. 1) и внутренность его, т. е. круг, за исключением ограничивающей его окружности, называют «плоскостью». Лобачевский ,как бы рассматривает геометрию сразу в масштабе нашей планеты.

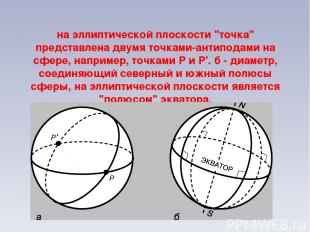
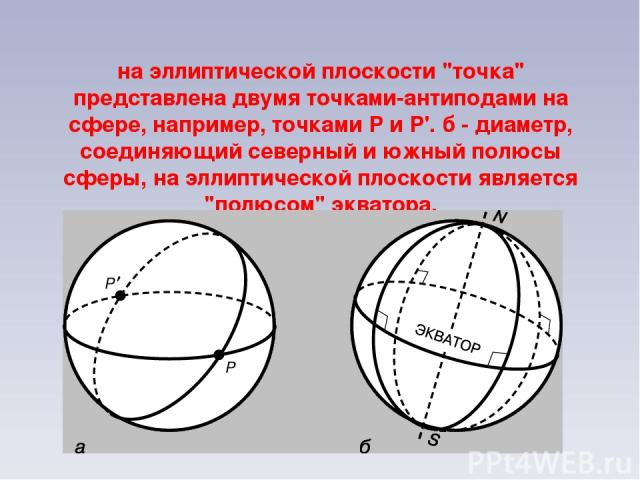
на эллиптической плоскости "точка" представлена двумя точками-антиподами на сфере, например, точками P и P'. б - диаметр, соединяющий северный и южный полюсы сферы, на эллиптической плоскости является "полюсом" экватора.

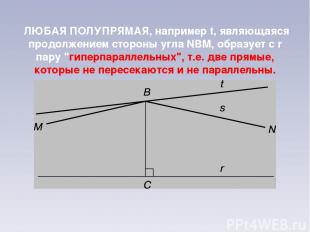
ЛЮБАЯ ПОЛУПРЯМАЯ, например t, являющаяся продолжением стороны угла NBM, образует с r пару "гиперпараллельных", т.е. две прямые, которые не пересекаются и не параллельны.

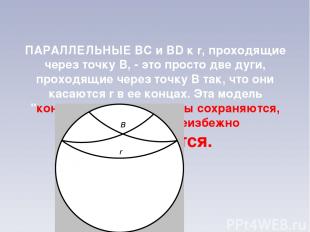
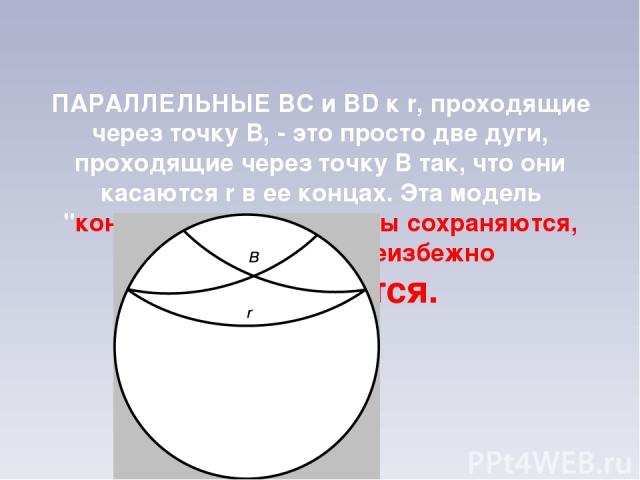
ПАРАЛЛЕЛЬНЫЕ BC и BD к r, проходящие через точку B, - это просто две дуги, проходящие через точку B так, что они касаются r в ее концах. Эта модель "конформна", так как углы сохраняются, хотя расстояния неизбежно искажаются.

АКСИОМА 1 Через любые две точки проходит прямая и притом только одна

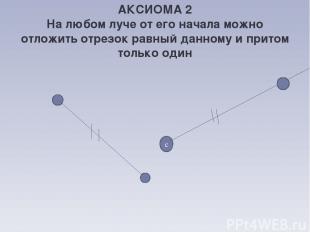
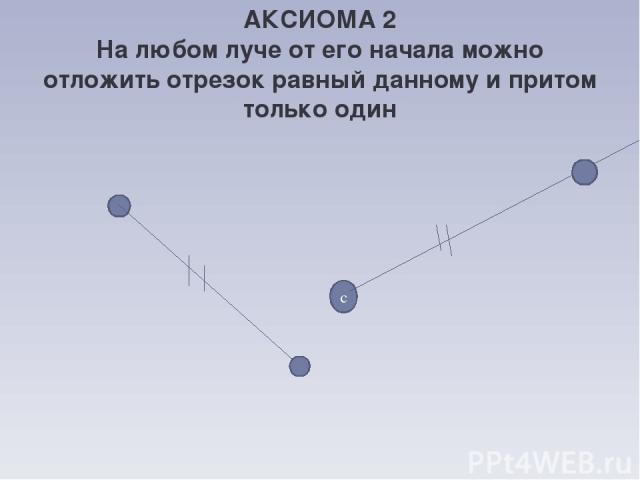
АКСИОМА 2 На любом луче от его начала можно отложить отрезок равный данному и притом только один с

АКСИОМА 3 От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.

Аксиома 4 Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствие 1 Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. c a b

Следствие 2 Если две прямые параллельны третей прямой, то они параллельны а c b