Презентация на тему: Аксиомы в геометрии

Аксиомы в гкометрии

В “Началах” был развит аксиоматический подход к построению геометрии, который состоит в том, что сначала формулируются основные положения (аксиомы), а затем на их основе посредством рассуждений доказываются другие утверждения (теоремы). Изложение геометрии Евклидом долгое время служило недосягаемым образцом точности, безукоризненности и строгости. Только в начале 20 века математики смогли улучшить логические основания геометрии.

Как формулируется равносильная аксиома параллельности? Аксиома параллельных прямых. Через любую точку, лежащую вне прямой, можно провести другую прямую, параллельную данной, и притом только одну.
рхимедова аксиома Для отрезков, аксиома Архимеда звучит так: если даны два отрезка, то отложив достаточное количество раз меньшего из них, можно покрыть больший.

Аксиома порядка. Среди любых трёх точек, лежащих на прямой, есть не более одной точки, лежащей между двух других.
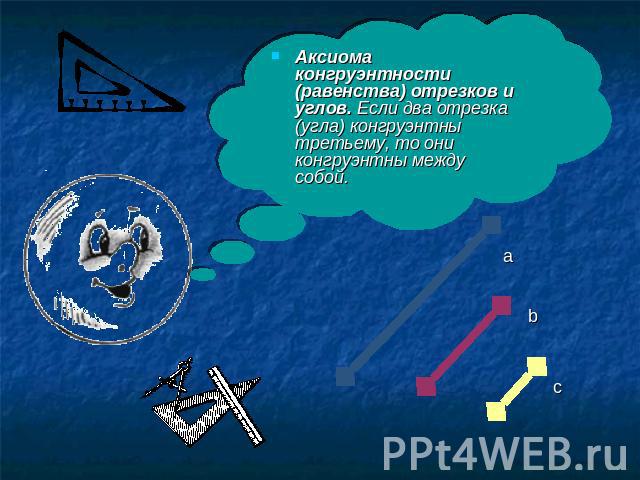
Аксиома конгруэнтности (равенства) отрезков и углов. Если два отрезка (угла) конгруэнтны третьему, то они конгруэнтны между собой.

Аксиома принадлежности. Через любые две точки на плоскости можно провести прямую и притом только одну.

ксиома откладывания На любой полупрямой от ее начальной точки можно отложить отрезок, заданной длины, и только один.
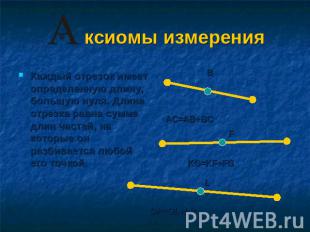
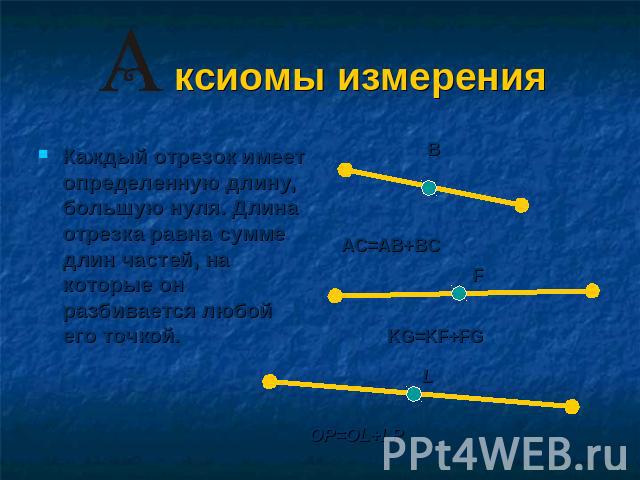
ксиомы измерения Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Следует подчеркнуть, что замена одной из этих аксиом на другую, превращает её в теорему, уже требующую доказательства. Так, вместо аксиомы параллельных прямых можно использовать в качестве аксиомы свойство углов треугольника («сумма углов треугольника равна 180º »). Но тогда необходимо доказывать аксиому о параллельных прямых.