Презентация на тему: Сумма углов треугольника

«Сумма углов треугольника»Разработчик: учитель математики МОУ СОШ № 2 города РадужныйМишурова Любовь Александра

.Данные слайды используются при рассмотрении теоретического материала по теме: соотношения между сторонами и углами треугольника.

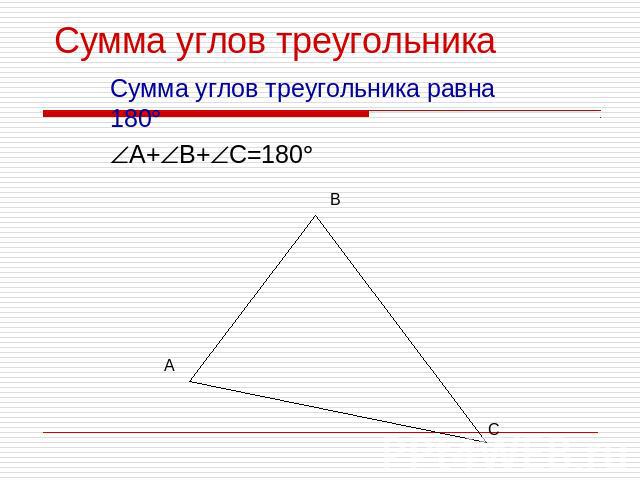
Сумма углов треугольникаСумма углов треугольника равна 180А+В+С=180

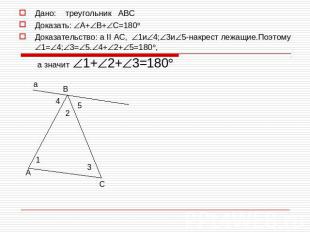
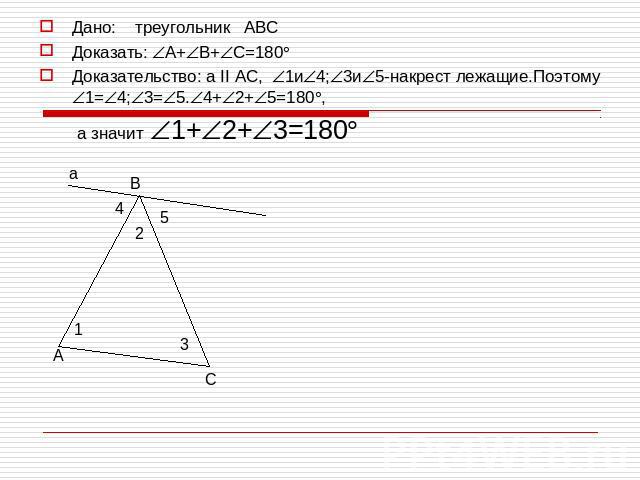
Дано: треугольник АВСДоказать: А+В+С=180Доказательство: а II АС, 1и4;3и5-накрест лежащие.Поэтому 1=4;3=5.4+2+5=180, а значит 1+2+3=180

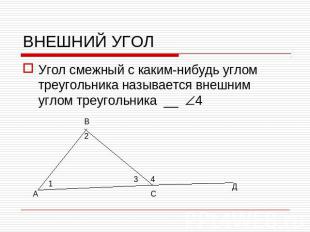
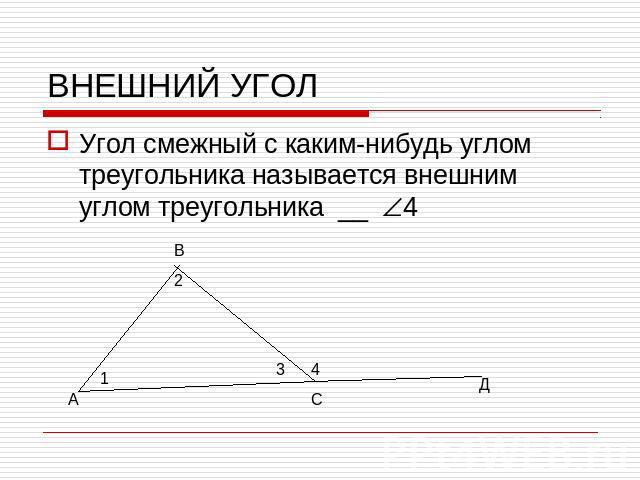
ВНЕШНИЙ УГОЛУгол смежный с каким-нибудь углом треугольника называется внешним углом треугольника __ 4

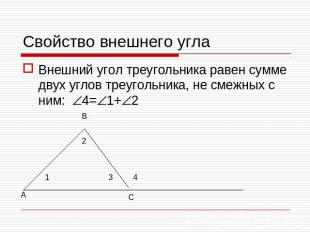
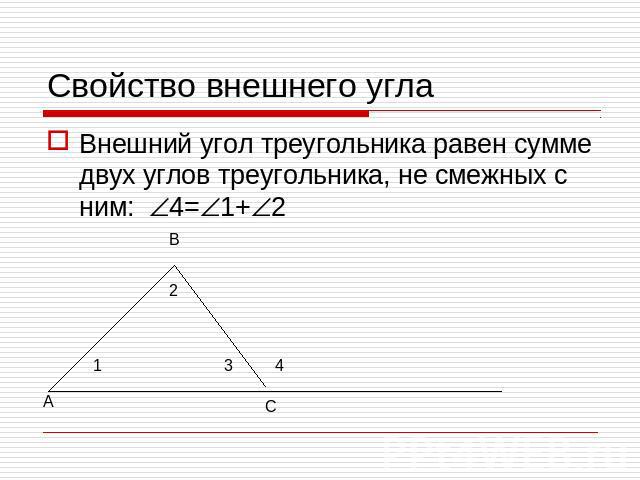
Свойство внешнего углаВнешний угол треугольника равен сумме двух углов треугольника, не смежных с ним: 4=1+2

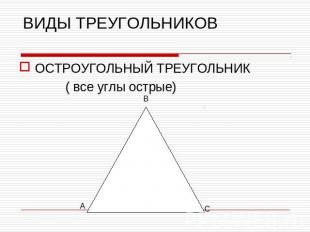
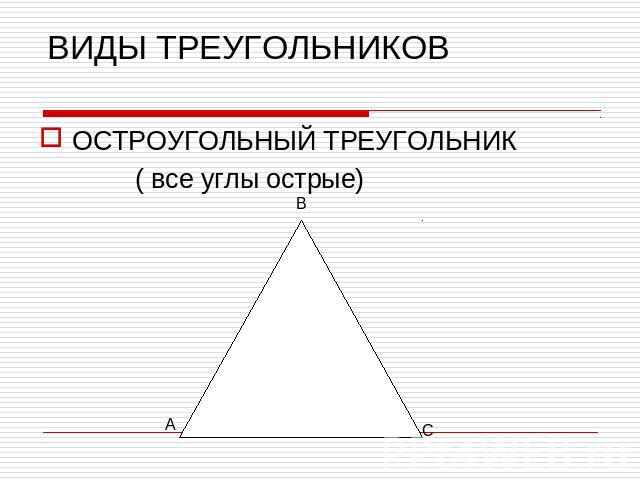
ВИДЫ ТРЕУГОЛЬНИКОВОСТРОУГОЛЬНЫЙ ТРЕУГОЛЬНИК ( все углы острые)

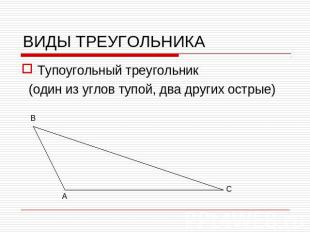
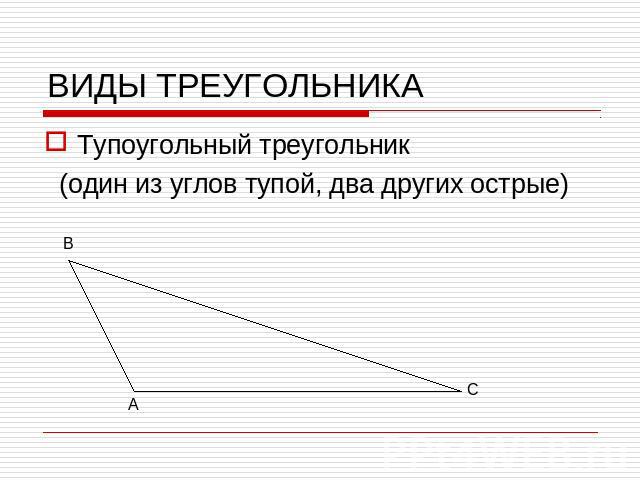
ВИДЫ ТРЕУГОЛЬНИКАТупоугольный треугольник (один из углов тупой, два других острые)

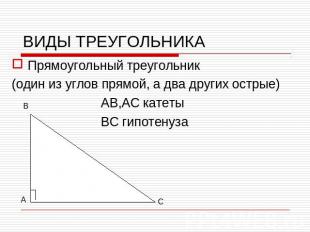
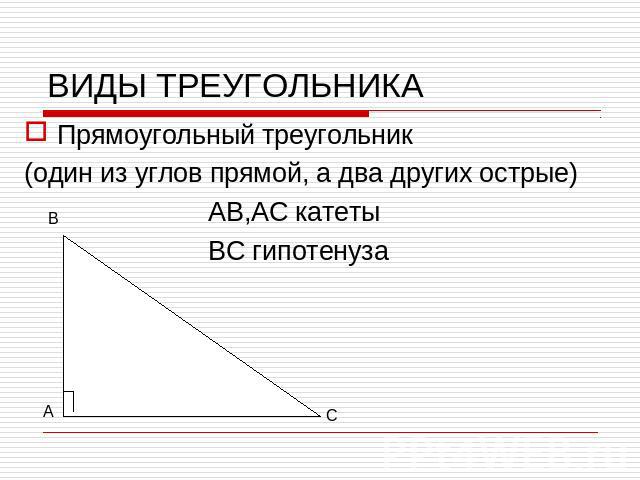
ВИДЫ ТРЕУГОЛЬНИКАПрямоугольный треугольник(один из углов прямой, а два других острые) АВ,АС катеты ВС гипотенуза

Соотношения между сторонами и углами треугольникаВ треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона. 1)АС большая сторона, значит В больший. 2)В большей, значит АС большая сторона.

СЛЕДСТВИЯ. В прямоугольном треугольнике гипотенуза больше катета.Если в треугольнике два угла равны, то треугольник равнобедренный( признак равнобедренного треугольника).

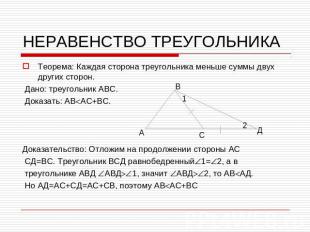
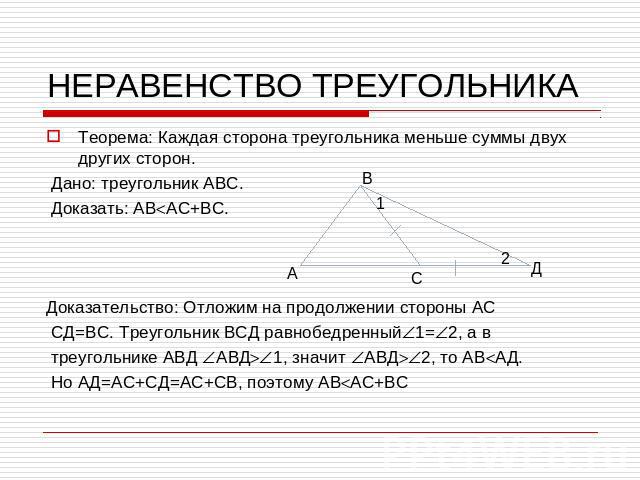
НЕРАВЕНСТВО ТРЕУГОЛЬНИКАТеорема: Каждая сторона треугольника меньше суммы двух других сторон. Дано: треугольник АВС. Доказать: АВАС+ВС. Доказательство: Отложим на продолжении стороны АС СД=ВС. Треугольник ВСД равнобедренный1=2, а в треугольнике АВД АВД1, значит АВД2, то АВАД. Но АД=АС+СД=АС+СВ, поэтому АВАС+ВС

СЛЕДСТВИЕДЛЯ ЛЮБЫХ ТРЁХ ТОЧЕК А,В И С, не лежащих на одной прямой, справедливы неравенства: АВ АС+ВС; АС АВ+ВС; ВС ВА+АС.

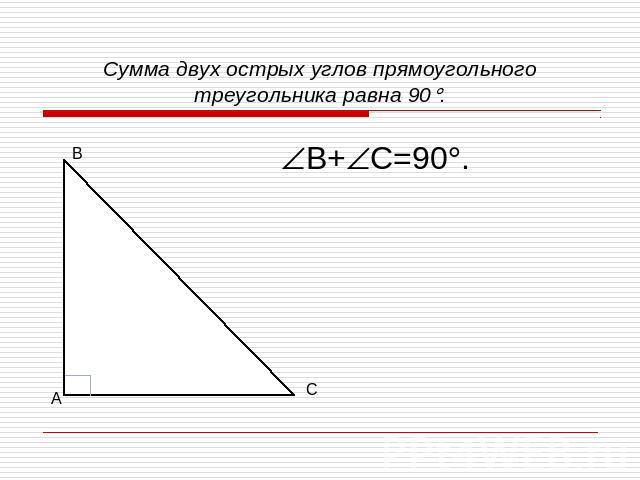
ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ(свойства)1. Сумма двух острых углов прямоугольного треугольника равна 90.2. Катет прямоугольного треугольника, лежащий против угла в 30, равен половине гипотенузы. 3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30.

Сумма двух острых углов прямоугольного треугольника равна 90.

Катет прямоугольного треугольника, лежащего против угла в 30, равен половине гипотенузы.Рассмотрим треугольник АВС, где А=90, В=30 и С=60. Докажем, что АС=½ВС. Приложим к треугольнику АВС равный ему треугольник АВД. Получим треугольник ВСД, В=Д=60, поэтому ДС = ВС, но АС= ½ ДС, значит АС = ½ ВС.

Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30.которого катет АС равен половине гипотенузы ВС. Докажем, что АВС=30 Приложим к треугольнику АВС равный ему треугольник АВД, получим равно- сторонний треугольник ВСД, где Д=С=ДВС=60. ДВС=2АВС, следовательно, АВС=30.

Признаки равенства прямоугольных треугольников.Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

Признаки равенства прямоугольных треугольников.Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.

Признаки равенства прямоугольных треугольников.Если гипотенуза и острый угол одного прямоугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.

Признаки равенства прямоугольных треугольниковЕсли гипотенуза и катет одного прямоугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.