Презентация на тему: Движение фигур в стереометрии

Проект по геометрии на тему: «Движение фигур в стереометрии»Выполнила: ученица 9в классаМОУ СОШ № 21Шевяхова ВикторияПроверила:Мариничева Ирина Михайловна

Определение движенияДвижение – геометрическое преобразование, при котором сохраняются расстояния между точками.Движением (или перемещением) фигуры называется такое ее отображение, при котором каждым двум ее точкам A и B соответствуют такие точки A’ и B’, что |A’B’| = |AB|.

Виды движениЯПОВОРОТЦЕНТРАЛЬНАЯ СИММЕТРИЯПараллельный переносПОДОБИЕВЫВОДЫСПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

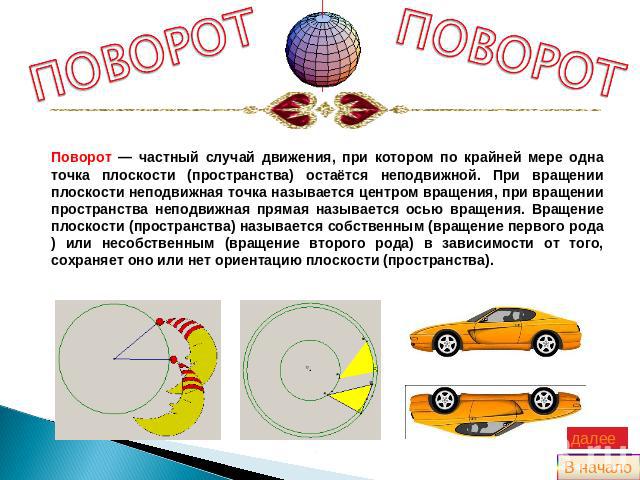
ПОВОРОТПОВОРОТПоворот — частный случай движения, при котором по крайней мере одна точка плоскости (пространства) остаётся неподвижной. При вращении плоскости неподвижная точка называется центром вращения, при вращении пространства неподвижная прямая называется осью вращения. Вращение плоскости (пространства) называется собственным (вращение первого рода) или несобственным (вращение второго рода) в зависимости от того, сохраняет оно или нет ориентацию плоскости (пространства).

Центральной симметрией относительно точки A называют преобразование плоскости, переводящее точку X в такую точку X', что A — середина отрезка XX'. Центральная симметрия с центром в точке A обычно обозначается через ZA, в то время как обозначение SA можно перепутать с осевой симметрией.

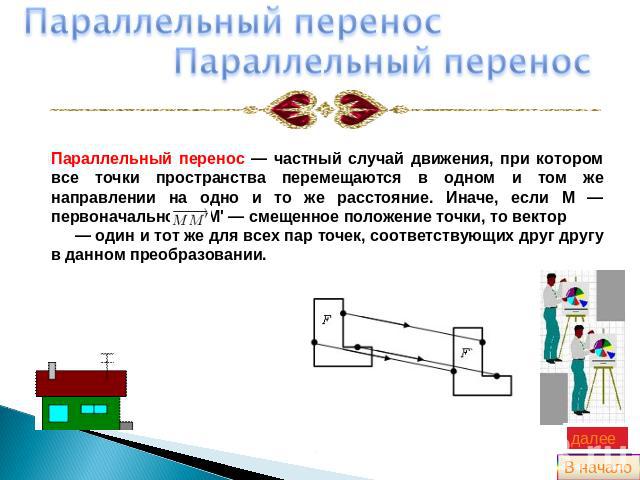
Параллельный переносПараллельный переносПараллельный перенос ― частный случай движения, при котором все точки пространства перемещаются в одном и том же направлении на одно и то же расстояние. Иначе, если M ― первоначальное, а M' ― смещенное положение точки, то вектор ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании. 

ПОДОБИЕПОДОБИЕ Подобие - биективное преобразование с особыми свойствами. 

ВыводыПри движении три точки, лежащие на прямой, переходят в три точки, лежащие на прямой, причем точка, лежащая между двумя другими, переходит в точку, лежащую между образами двух других точек (сохраняется порядок их взаимного расположения).Образом отрезка при движении является отрезок.Образом прямой при движении является прямая, а образом луча - луч.При движении образом треугольника является равный ему треугольник, образом плоскости - плоскость, причем параллельные плоскости отображаются на параллельные плоскости, образом полуплоскости - полуплоскость.При движении образом тетраэдра является тетраэдр, образом пространства - все пространство, образом полупространства - полупространство.При движении углы сохраняются, т.е. всякий угол отображается на угол того же вида и той же величины. Аналогичное верно и для двугранных углов.

Список использованных источниковhttp://ru.wikipedia.orghttp://fizika.asvu.ruЯзык науки: Пер. с англ./Предисл.Б. Д. Сергиевского. – М.: Мир, 1985