Презентация на тему: Пирамиды

Пирамиды

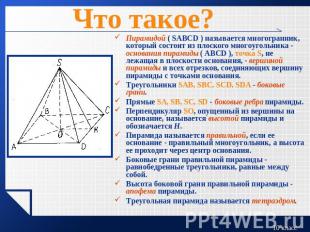
Что такое?Пирамидой ( SABCD ) называется многогранник, который состоит из плоского многоугольника - основания пирамиды ( ABCD ), точка S, не лежащая в плоскости основания, - вершиной пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Треугольники SAB, SBC, SCD, SDA - боковые грани. Прямые SA, SB, SC, SD - боковые ребра пирамиды. Перпендикуляр SO, опущенный из вершины на основание, называется высотой пирамиды и обозначается Н. Пирамида называется правильной, если ее основание - правильный многоугольник, а высота ее проходит через центр основания. Боковые грани правильной пирамиды - равнобедренные треугольники, равные между собой. Высота боковой грани правильной пирамиды - апофема пирамиды. Треугольная пирамида называется тетраэдром.

Правильная пирамидаОтметим некоторые свойства правильной n-угольной пирамиды на примере треугольной пирамиды.Как известно центр правильного треугольника совпадает с центром вписанной и описанной окого него окружности. Поэтому отрезки АО, ВО и СО равны как радиусы.Поэтому прямоугольные треугольники АОМ, ВОМ и СОМ равны по двум катетам (МО-общая). Из равенства этих треугольников следует равенство соответствующих сторон: АМ=ВМ=СМСвойство 1: В правильной n-угольной пирамиде все боковые ребра равны между собой.Из равенства ребер следует и равенство боковых граней. Треугольники АВМ, ВСМ и АСМ равны по трем сторонам.Свойство 2: Все боковые грани правильной n-угольной пирамиды суть равные равнобедренные треугольники, поэтому все плоские углы при вершине равны, все плоские углы при основании равны.Из равенства прямоугольных треугольников ОРМ, ОТМ и ОКМ (ОТ=ОР=ОК как радиусы вписанной окружности; МО - общая) следует равенство всех двугранных углов при основании пирамиды РОРМ=РОТМ=РОКМСвойство 3: В правильной n-угольной пирамиде все двугранные углы при основании равны.

Формулы для пирамидПлощадью полной поверхности пирамиды называется сумма площадей всех её гранейSполн=Sбок+Sосн;Площадь боковой поверхности пирамиды – сумма площадей её боковых граней;Площадь боковой грани Sбок.гр=1/2 x mx\g\, где m – апофема, \g\ - основание грани;Теорема: Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофемуSбок=1/2 x(Pосн x m),где m – апофема, Р – периметр многоугольника основания;Объём пирамиды V=(1/3) x Sосн x h.

ЗадачаЗадача1: Основание пирамиды – треугольник, две стороны которого равны 1 и 2, а угол между ними равен 60˚. Каждое боковое ребро равно √13 . Найдите объем пирамиды.Решение. Так как все ребра (боковые) пирамиды равны, они одинаково наклонены к основанию, и вершина пирамиды проектируется в центр описанной вокруг основания окружности. (см. чертеж).Объем пирамиды: , ,Высоту SO можно найти по т. Пифагора например, из треугольника ASO. Для этого нужно найти AO – радиус описанной окружности основания.Воспользуемся теоремой синусов: .Но сначала по теореме косинусов найдем сторону BC: , BC= .Теперь вычислим радиус описанной окружности:Найдем SO: .Вычислим объем: .Ответ: V=1.

А под конец…Слово «пирамида» в геометрию ввели греки,которые, как полагают, заимствовали егоу египтян, создавших самые знаменитыепирамиды в мире. Другая теория выводитэтот термин из греческого слова «пирос»(рожь) – считают, что греки выпекали хлебцы,имевшие форму пирамиды