Презентация на тему: Наибольшее и наименьшее значение функции

Наибольшее и наименьшее значение функции

Цель урока: Применение производной к нахождению наибольших и наименьших значений функций, к решению простейших прикладных задач «на экстремум»:Алгебраического смысла;Геометрического смысла.

«Идея функциональной зависимости в чистом виде выступает в тот момент, когда появляется алгебраическая формула или «алгебраическое выражение»».Дубнов Я.С.
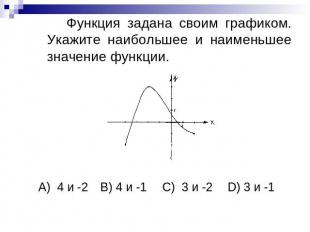
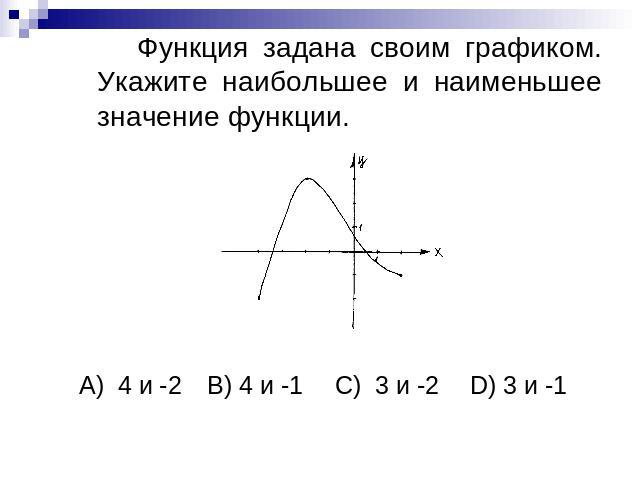
Функция задана своим графиком. Укажите наибольшее и наименьшее значение функции.А) 4 и -2B) 4 и -1C) 3 и -2 D) 3 и -1

Найдите наибольшее значение функции f(x)=5-х2А) -11B) 8C) 4 D) 5

3. Найдите наименьшее значение функции f(x)= 3 sin x на отрезке .

4.Какая из функций имеет максимум?А) y =x3 B) y=C) y= D) y= 2x-x2

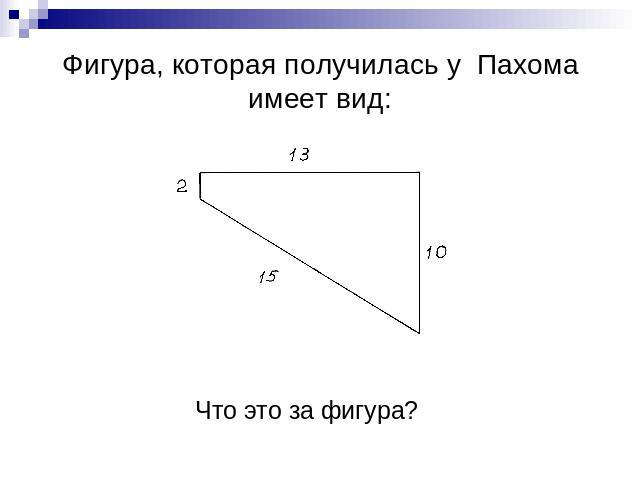
Рассказ «Много ли человеку земли нужно» О крестьянине Пахоме, покупавшем землю у башкирцев. -А цена какая будет?- говорит Пахом. -Цена у нас одна: 1000 рублей за день. Не понял Пахом. -Какая же это мера – день? Сколько в ней десятин будет? -Мы этого, - говорит, - не умеем считать. А мы за день продаем; сколько обойдешь в день, то и твое, а цена 1000 рублей. Удивился Пахом. -Да ведь это, - говорит, -в день обойти земли много будет. Засмеялся старшина. -Вся твоя, - говорит. – Только один уговор: если назад не придешь в день к тому месту, с какого возьмешься, пропали твои деньги. -А как же, - говорит, - отметить , где я пройду? -А мы встанем на место, где ты облюбуешь; мы стоять будем, а ты иди, делай круг, а с собой скребку возьми и, где надобно, замечай, на углах ямки рой, дернички клади; потом с ямки на ямку плугом пройдем. Какой хочешь круг забирай, только до захода солнца приходи к тому месту, с какого взялся. Что обойдешь, все твое.Л.Н. Толстой

Фигура, которая получилась у Пахома имеет вид:Что это за фигура?

Задача: Периметр прямоугольника равен 60см. Какую длину должны иметь стороны прямоугольника, чтобы площадь была наибольшей?

Задача: На параболе y=x2 найдите точку, ближайшую к точке А(2; 0,5)

«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!»«Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдется путь!»Пойа Д.