Презентация на тему: Смежные и вертикальные углы

Урок 11 Смежные и вертикальные углы
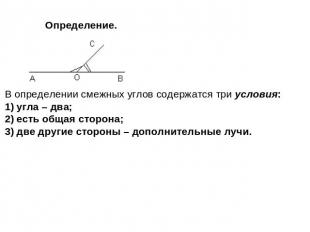
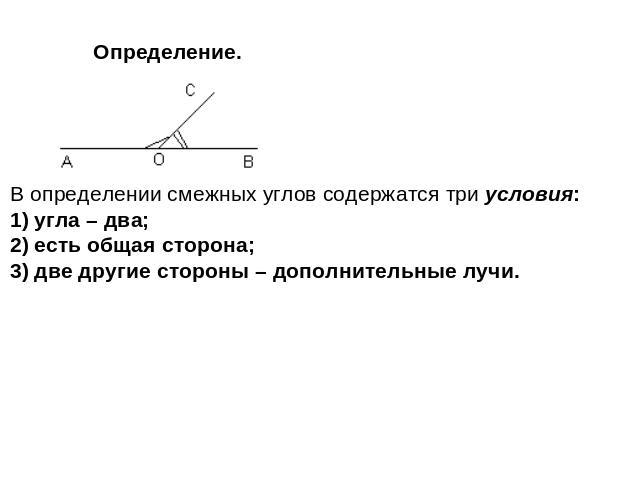
Урок 11 Смежные и вертикальные углы Определение. В определении смежных углов содержатся три условия: угла – два; есть общая сторона; две другие стороны – дополнительные лучи.
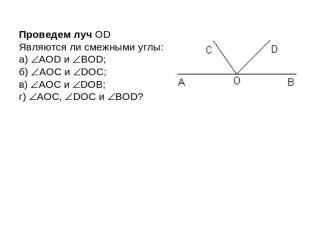
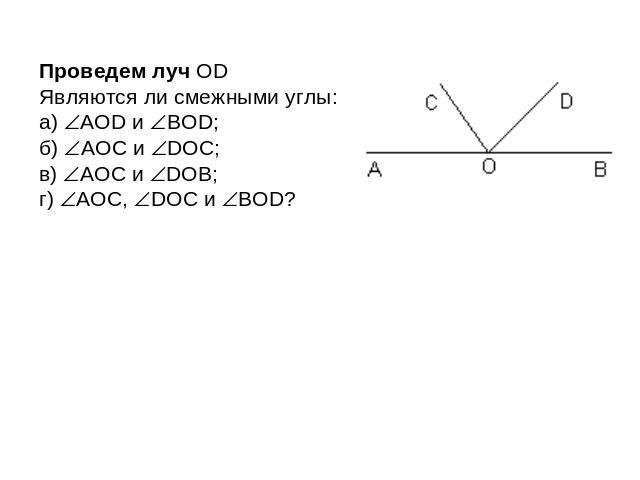
Проведем луч OD Являются ли смежными углы: а) AOD и BOD; б) AOС и DOС; в) AOС и DOВ; г) AOС, DOС и BOD?
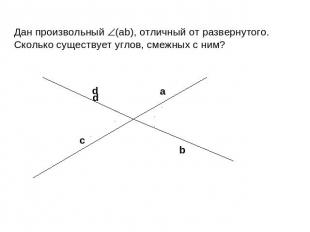
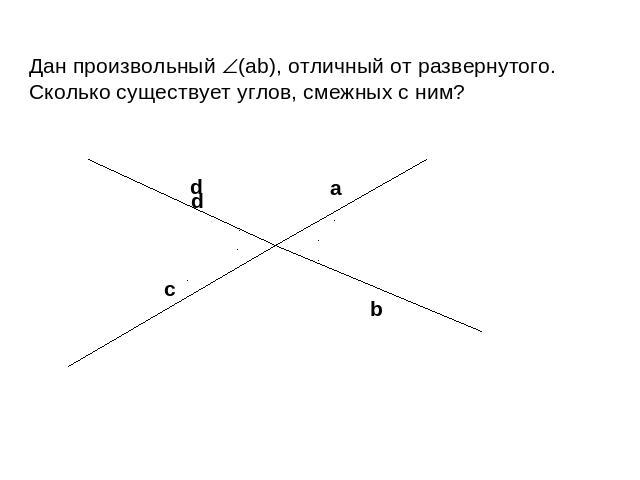
Дан произвольный (аb), отличный от развернутого. Сколько существует углов, смежных с ним?
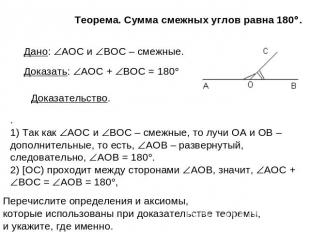
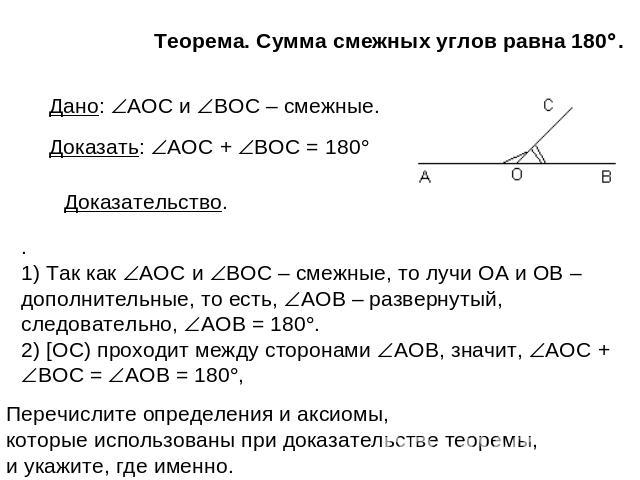
Теорема. Сумма смежных углов равна 180. Дано: AOC и BOC – смежные. Доказать: AOC + BOC = 180 Доказательство. . 1) Так как AOC и BOC – смежные, то лучи ОА и ОВ – дополнительные, то есть, AOB – развернутый, следовательно, AOB = 180. 2) [OC) проходит между сторонами AOB, значит, AOC + BOC = AOB = 180, Перечислите определения и аксиомы, которые использованы при доказательстве теоремы, и укажите, где именно.

Следствия из теоремы 1) Углы, смежные равным углам, равны между собой. 2) Угол, смежный прямому углу – прямой, смежный острому – тупой, смежный тупому – острый. А смежный развернутому?
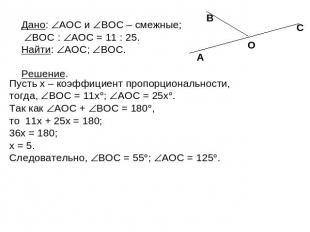
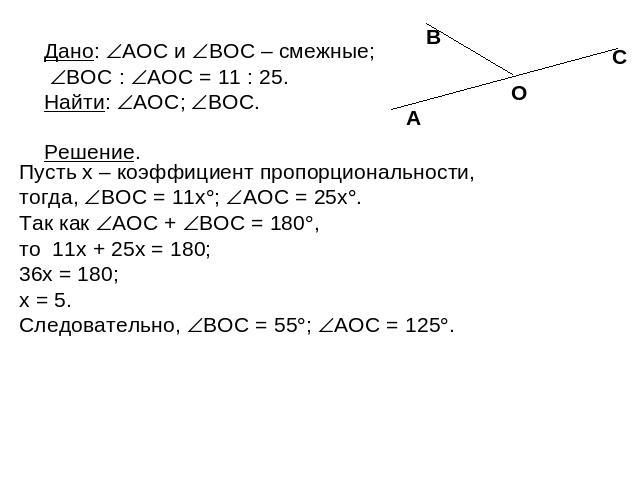
Дано: AOC и BOC – смежные; BOC : AOC = 11 : 25. Найти: AOC; BOC. Пусть x – коэффициент пропорциональности, тогда, BOC = 11x; AOC = 25x. Так как AOC + BOC = 180, то 11x + 25x = 180; 36x = 180; x = 5. Следовательно, BOC = 55; AOC = 125.

Сформулируйте утверждение, обратное теореме о смежных углах. Верно ли оно? Станет ли оно верным, если добавить, что у данных углов есть общая сторона? Что еще необходимо добавить в условие, чтобы оно стало верным?
Вертикальные углы
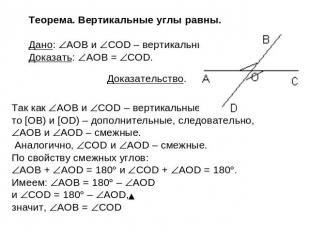
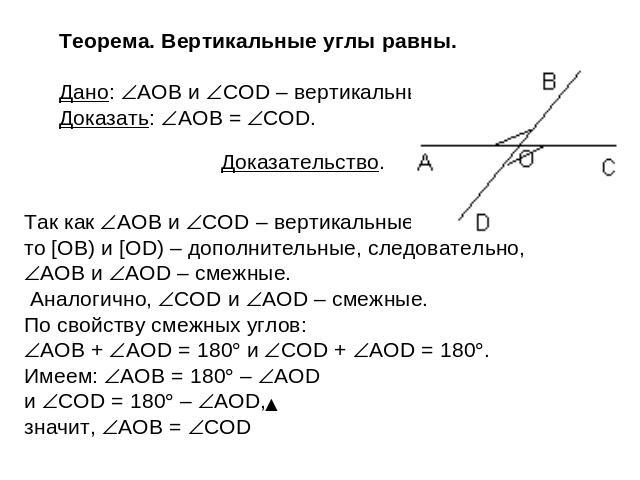
Теорема. Вертикальные углы равны. Дано: AOB и COD – вертикальные. Доказать: AOB = COD. Доказательство. Так как AOB и COD – вертикальные, то [OB) и [OD) – дополнительные, следовательно, AOB и AOD – смежные. Аналогично, COD и AOD – смежные. По свойству смежных углов: AOB + AOD = 180 и COD + AOD = 180. Имеем: AOB = 180 – AOD и COD = 180 – AOD, значит, AOB = COD

Сформулируйте утверждение, обратное свойству вертикальных углов. Верно ли оно?

Сумма трех углов (отличных от развернутого), образовавшихся при пересечении двух прямых, равна 205. Найдите эти углы Дано: (МК) (PN) = O; POK + POM + NOM = 205. Найти: РOK; POM; NOM. Решение. Из трех данных углов два являются смежными, например, POK и POM. POK + POM = 180, значит, NOM = 205 – 180 = 25. POK = NOM = 25, так как эти углы – вертикальные. POM = 180 – POK = 155. Ответ: два угла по 25 и один – 155.