Презентация на тему: Пирамиды

ПИРАМИДА МОУ СОШ №5 – «Школа здоровья и развития» г. Радужный Автор: Карсанова Алина, ученица 10Б класса 900igr.net

Содержание Определение пирамиды Площадь пирамиды Правильная пирамида Свойство пирамиды Апофема Теорема о площади боковой поверхности правильной пирамиды Усеченная пирамида Правильная усеченная пирамида Теорема о площади боковой поверхности правильной усеченной пирамиды

Определение Пирамида – многогранник, составленный из n - угольника А1А2…Аn и n треугольников Высота – перпендикуляр, проведенный из вершины пирамиды к плоскости основания Боковые ребра

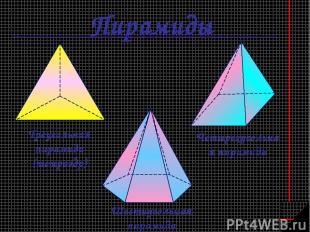
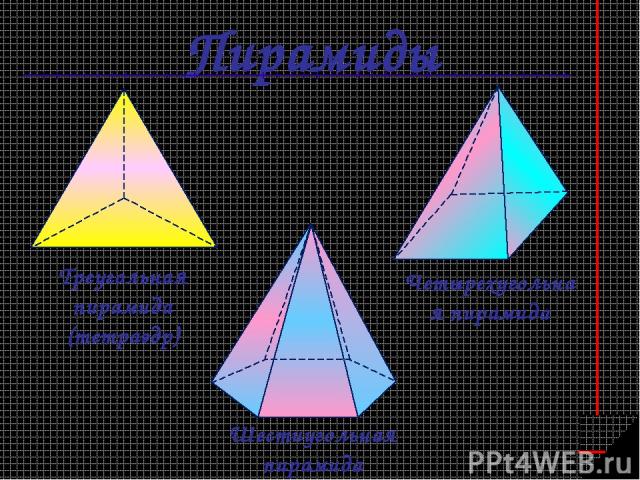
Пирамиды Треугольная пирамида (тетраэдр) Шестиугольная пирамида Четырехугольная пирамида

Площадь пирамиды Sполн. = Sбок. + Sосн. Sбок. Sосн.

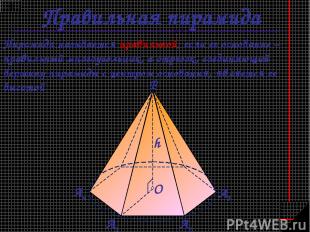
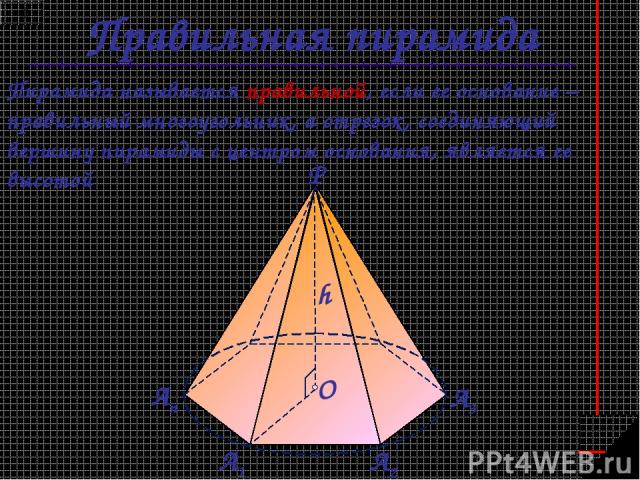
Правильная пирамида Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой

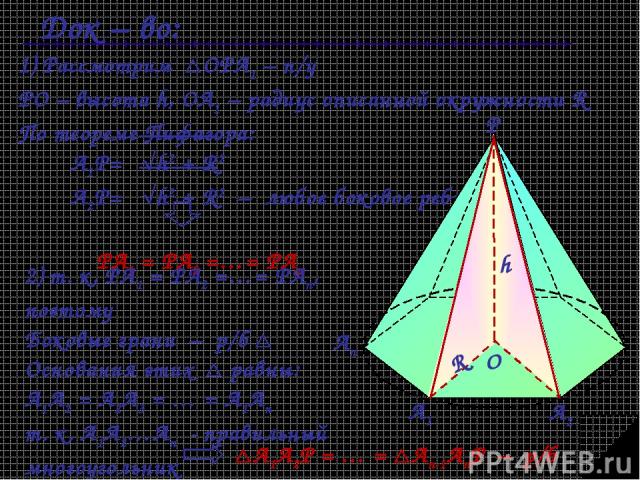
Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками Дано: PA1A2…An – правильная пирамида Док - ть: 1) А1Р = А2Р = … = АnР 2) А1А2Р = А2А3Р = … = = Аn-1АnР – р/б

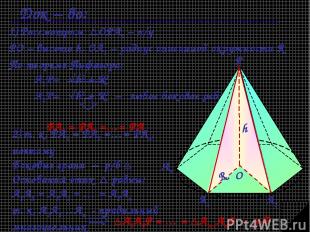
Док – во: 2) т. к. РА1 = РА2 =…= РАn, поэтому Боковые грани – р/б Основания этих равны: А1А2 = А2А3 = … = А1Аn т. к. А1А2…Аn - правильный многоугольник А1А2Р = … = Аn-1АnР – р/б

Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины Апофемы Все апофемы правильной пирамиды равны друг другу

Теорема о площади боковой поверхности правильной пирамиды Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему Док – во: Sбок = (½ad + ½ad + ½ad) = = ½d(a + a + a)= ½dP Sбок = ½dP

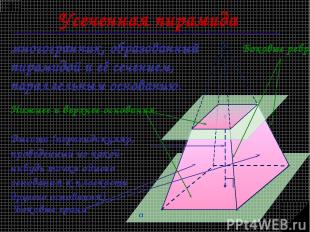
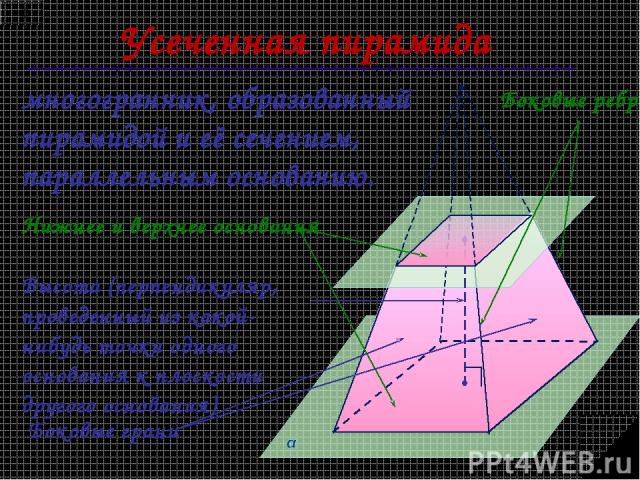
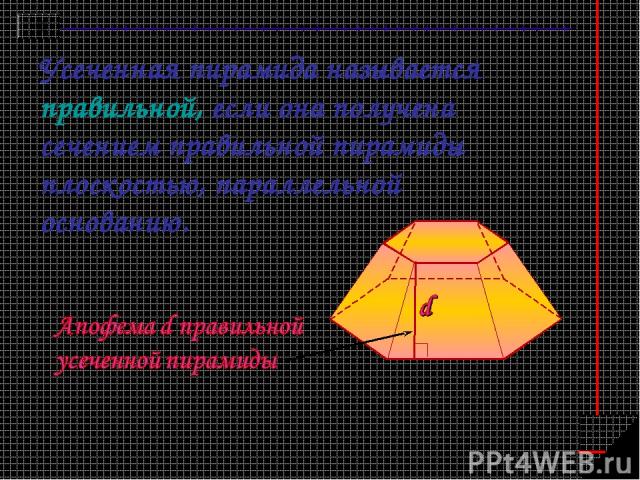
Усеченная пирамида многогранник, образованный пирамидой и её сечением, параллельным основанию. Нижнее и верхнее основания Боковые грани Боковые ребра Высота (перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания)

Все боковые грани усеченной пирамиды - трапеции

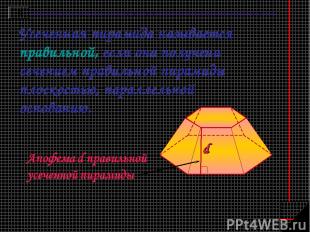
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Теорема о площади боковой поверхности правильной усеченной пирамиды Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему S бок = ½(Р1 + Р2) d P1= 4a1 P2= 4a2 Док – во: S бок = ½d(a1+a2) + ½d(a1+a2) + + ½ d(a1+a2) + ½d(a1+a2) = = ½d(a1+ a2+ a1+ a2+ a1+ a2+ a1+ a2) = = ½d(4a1+ 4a2) = ½d(P1+ P2)

Презентация подготовлена по материалам сайта http://ru.wikipedia.org учебника для общеобразовательных учреждений «Геометрия 10-11 классы» (Авторы Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Л. С. Киселева, Э. Г. Поздняк)