Презентация на тему: Пирамиды

Пирамиды.

Многопрофильная гимназия №79ОТКРЫТЫЙ УРОК«ГЕОМЕТРИЧЕСКАЯ ПИРАМИДА И ЕЁ ПРОЕКЦИЯ» Учитель: Волкова Лидия Николаевна Город Алматы 2009г.

Презентацию готовили Дасиева Роза,Набоко Михаил, Ибрагимова Карина, Егизбаева Айнура, Асанова Эльвира, Ускенбаева Мадия.

О слове пирамида. Пирамида.Слово «пирамида» в геометрию ввели греки,которые, как полагают, заимствовали егоу египтян, создавших самые знаменитыепирамиды в мире. Другая теория выводитэтот термин из греческого слова «пирос»(рожь) – считают, что греки выпекали хлебцы,имевшие форму пирамиды.

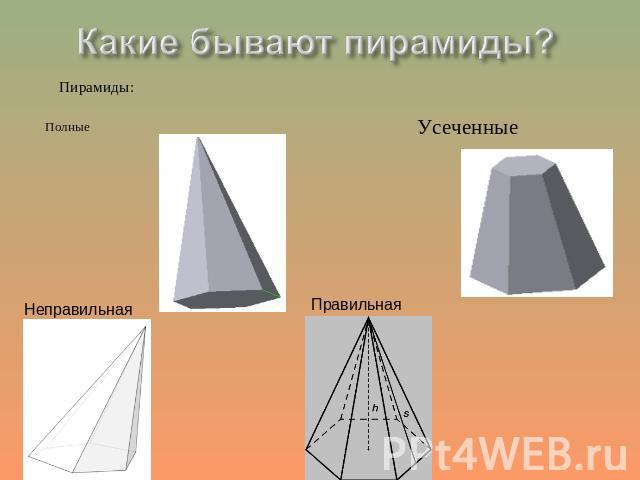
Что же такое пирамида? Пирамида- многогранник, у которого основание- многоугольник, боковые грани- треугольники, имеющие общую вершину.

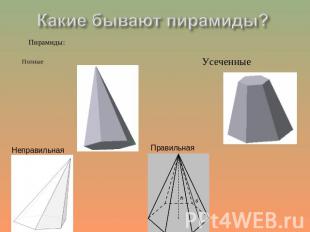
От чего зависит вид пирамиды? Вид пирамиды зависит от многоугольника, который лежит в основании.

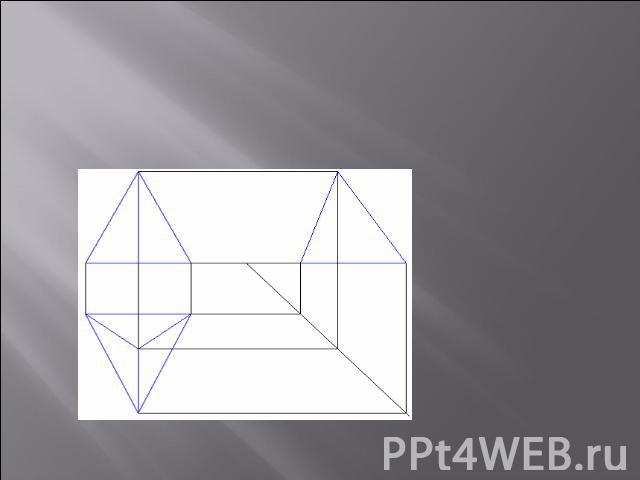
Проекция пирамиды Пирамида треугольная

Пирамида – это многогранник, одна из граней которого – произвольный n – угольник A1A2…An, а остальные грани – треугольники с общей вершиной. Этот n – угольник A1A2…An называется основанием пирамиды. Треугольные грани называются боковыми гранями. Общая вершина всех боковых граней называется вершиной пирамиды.Отрезки, соединяющие вершину пирамиды с вершинами основания называются боковыми рёбрами. Объединение боковых граней пирамиды называется её боковой поверхностью.Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды.ABCD – основание S – вершинаSO – высота

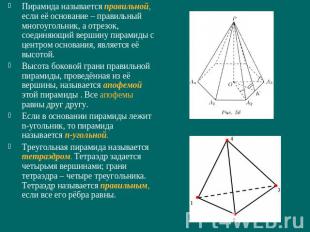
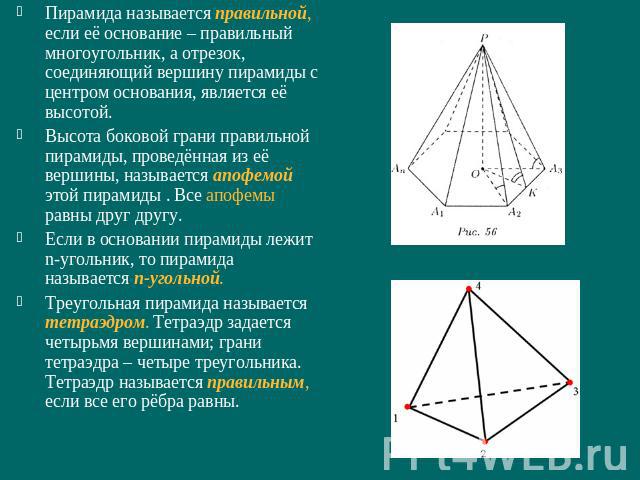
Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой этой пирамиды . Все апофемы равны друг другу.Если в основании пирамиды лежит n-угольник, то пирамида называется n-угольной.Треугольная пирамида называется тетраэдром. Тетраэдр задается четырьмя вершинами; грани тетраэдра – четыре треугольника. Тетраэдр называется правильным, если все его рёбра равны.

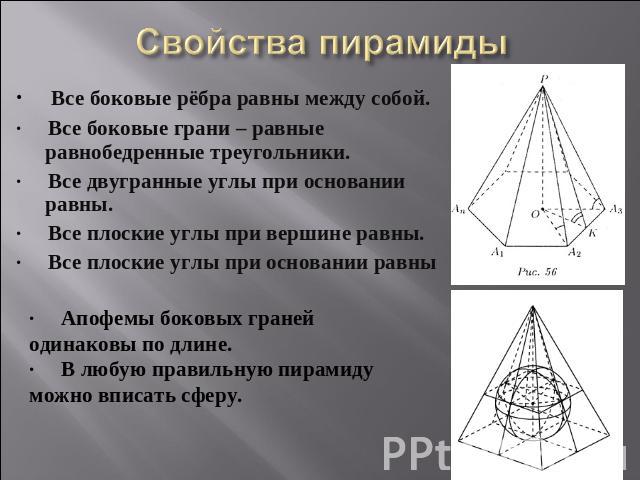
Свойства пирамиды ·     Все боковые рёбра равны между собой.·     Все боковые грани – равные равнобедренные треугольники.·     Все двугранные углы при основании равны.·     Все плоские углы при вершине равны.·     Все плоские углы при основании равны·     Апофемы боковых граней одинаковы по длине.·     В любую правильную пирамиду можно вписать сферу.

Площадь пирамиды Площадью полной поверхности пирамиды называется сумма площадей всех её граней. Sполн=Sбок+Sосн Площадь боковой поверхности пирамиды – сумма площадей её боковых граней.

Обьём пирамиды Объём пирамиды V=(1/3)*Sосн*h,где S – площадь основания, h – высота пирамиды.

Усечённая пирамида Усечённая пирамида – это часть пирамиды, лежащая между основанием и параллельным основанию сечением.Усечённая пирамида является частным случаем пирамиды.

Основания усечённой пирамиды – основание исходной пирамиды и многоугольник, полученный при пересечении её плоскостью (A1A2…An и B1B2…Bn). Отрезки A1B1, A2B2, …, AnBn называются боковыми рёбрами усечённой пирамиды. Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды. Боковые грани усечённой пирамиды – трапеции. Усечённую пирамиду с основаниями A1A2…An и B1B2…Bn обозначают так: A1A2…AnB1B2…Bn.Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усечённой пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами.

Свойства усечённой пирамиды. 1.    Боковые рёбра и высота пирамиды делятся секущей плоскостью на пропорциональные отрезки.2.    В сечении получается многоугольник, подобный многоугольнику, лежащему в основании.3.    Площади сечения и основания будут относится между собой, как квадраты их расстояний от вершины пирамиды.

Площадь поверхности правильной усечённой пирамиды: S=(1/2)*m*(P+P1), где m – апофема, P- периметр оснований, P1- периметр боковой поверхности. Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему: Sбок=1/2*(Рв+Рн)* m, где m – апофема, Рв, Рн – периметр верхнего и нижнего основанийОбъём усечённой пирамиды:V=(1/3)*h*(S1+√S1S2+S2), где S1, S2 – площади оснований.Площадь боковой грани:Sбок.гр.=1/2*m*(g+g1), гдеm – апофема, g, g1 – основания боковой грани.

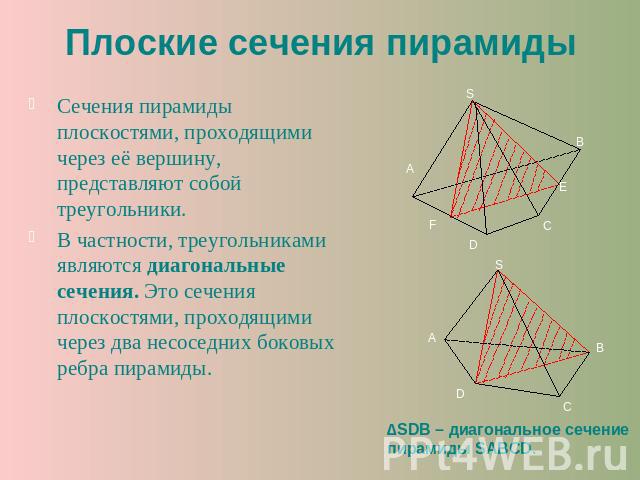
Плоские сечения пирамиды Сечения пирамиды плоскостями, проходящими через её вершину, представляют собой треугольники.В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два несоседних боковых ребра пирамиды.∆SDB – диагональное сечение пирамиды SABCD.

Построение сечения. Построить сечение четырехугольной пирамиды плоскостью, проходящей через прямую g и точку Е є пл.(SCD).

Построение сечения.Построить сечение четырехугольной пирамиды плоскостью, проходящей через прямую g и точку Е є пл.(SCD).

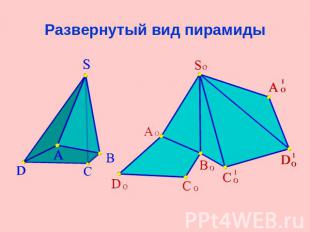
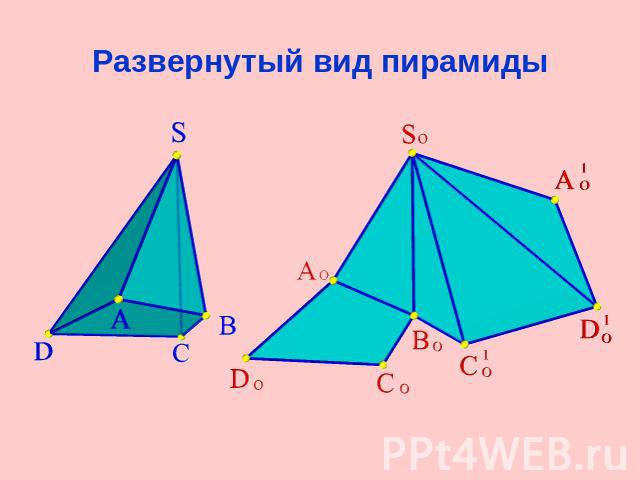
Развернутый вид пирамиды

ВСЕМ СПАСИБО!!!КОНЕЦ!