Презентация на тему: Множество

Множество Лобанова Лидия Павловна, 2011

Введение понятия множества Конечные множества Бесконечные множества

Введение понятия множества Множество Элемент множестваСпособы заданияПустое множество

Множество. Элемент множества. Способы задания. Множество – неопределяемое понятие. Некоторая совокупность элементов. Элементы – любые!Способы задания множеств: Перечисление элементов множества: A={1; 2; 3; 4; 5} Указание характеристических свойств элементов множества: В={х |х>0}

Примеры множеств A={1; 2; 3; 4; 5}Порядок элементов не важен!В – положительные числа

Равные множества Множество М ─ квадрат, трапеция, пятиугольник, круг, треугольник.Множество Р ─ круг, квадрат, треугольник, пятиугольник, трапеция.

Множества могут быть любые! Множество, в котором один элемент:птица Чир Множество цветовна школьной клумбе Пустое множество

Конечные множества Примеры Множество из 4 элементов: M={a;b;c;d} Множество цифр Множество букв русского алфавита Множество всех тигров, живущих на Земле

Примеры конечных множеств Множество всех цифрМножество гласных букв русского алфавита

Бесконечные множества Примеры Множество всех положительных чисел Множество всех точек на прямой Множество всех треугольников Множество всех фигур на плоскости

Числовые множества Важные примеры бесконечныхчисловыхмножеств

Числовые промежутки – множества, которые удобно рассматривать при решении неравенств.

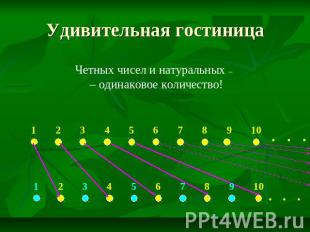
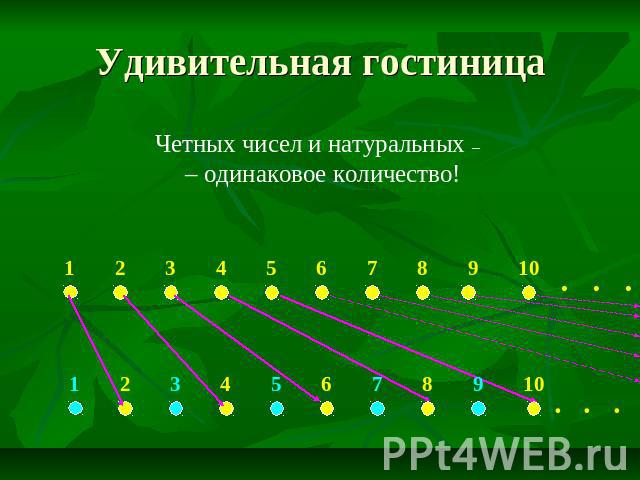
Удивительная гостиница Четных чисел и натуральных – – одинаковое количество!

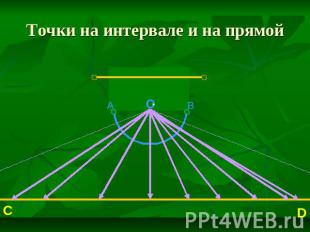
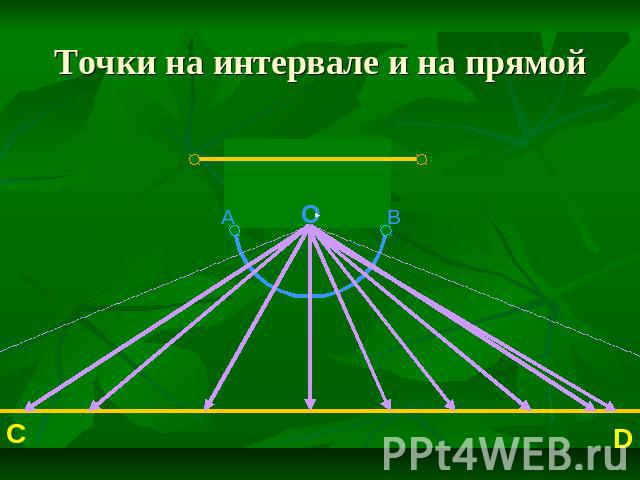
Точки на интервале и на прямой

Контрольные вопросы. Назовите элементы каждого множества.Назовите общие элементы этих множеств.Какие элементы множества А не принадлежат множеству В?Какие элементы множества В не принадлежат множеству А? Назовите элементы, которые входят хотя бы в одно из данных множеств.

Заключение Мы познакомилсь с некоторыми множествами и их элементами, и даже с пустым множеством. Узнали, что множества могут быть как конечными, так и бесконечными.Будем продолжать изучать множества!