Презентация на тему: Аксиомы стереометрии

Аксиомы стереометрии Учитель математики МБОУ «СОШ№31»г. Норильск Шеер Елена Анатольевна

Цели урока Повторить аксиомы планиметрииПознакомиться с аксиомами стереометрииУметь соотносить математическую формулировку аксиомы с графическим изображениемУметь формулировать ответы, используя строгость математического языкаПродолжать учиться работать в группахСовершенствовать навыки работы с тестами

Планиметрия Что изучает планиметрия?Как обозначают прямые и точки на плоскости?Какие аксиомы планиметрии вы помните?

Аксиома №1 Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

АксиомЙа №2 Через любые две точки можно провести прямую и только одну.

Аксиома №3 Из трех точек только одна лежит между двумя другими.

Аксиома №4 АС > 0; АС = АВ + ВС Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

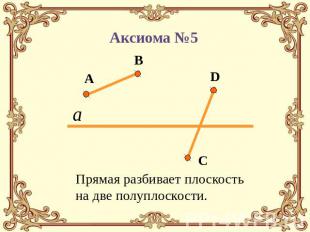
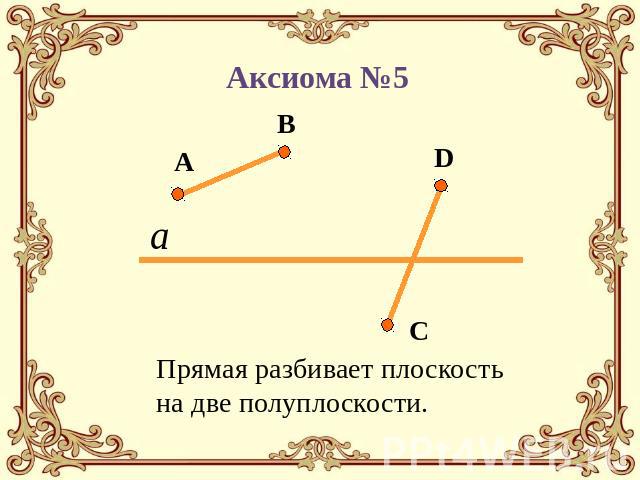
Аксиома №5 Прямая разбивает плоскость на две полуплоскости.

Аксиома №6 (ab)>0; (ac) = 180º(ac) = (ab) + (bc) Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180º. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

Аксиома №7 На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и только один.

Аксиома №8 На любой полупрямой от начальной точки можно отложить угол с заданной градусной меры, меньшей 180º и только один.

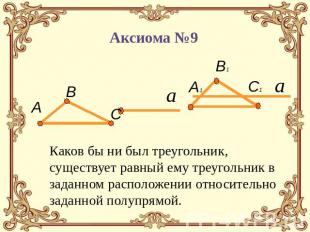
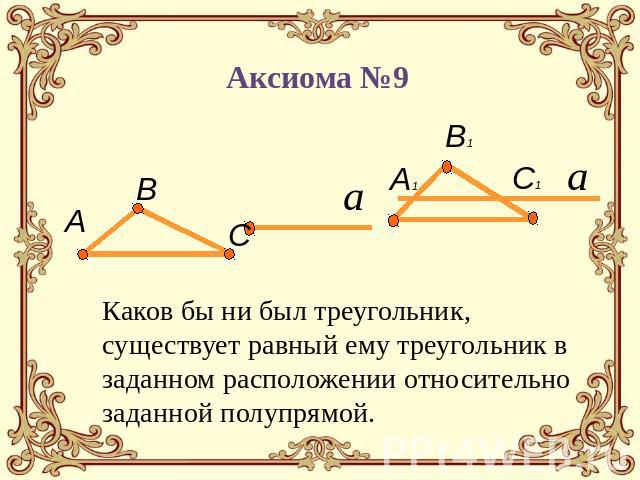
Аксиома №9 Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно заданной полупрямой.

Аксиома №10 Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Стереометрия Что изучает стереометрия?Основные фигуры в пространстве?Плоскость на рисунке изображается в виде…?Приведите примеры моделей плоскостей, окружающих нас.

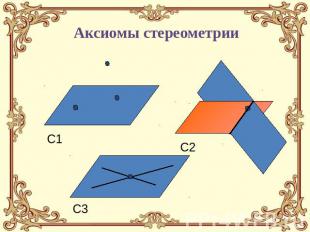
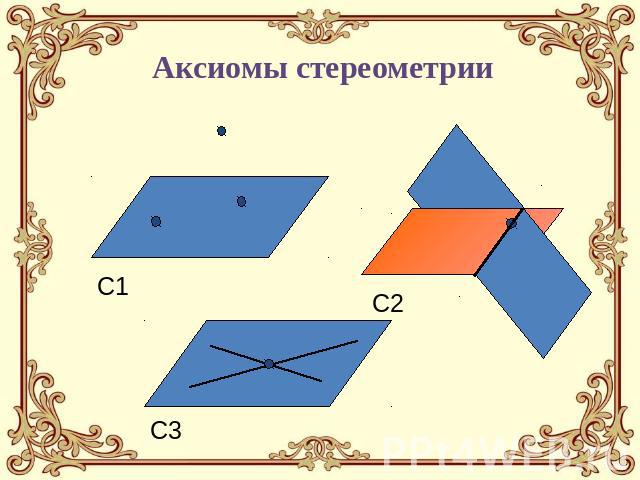
Аксиомы стереометрии

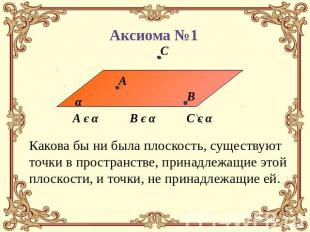
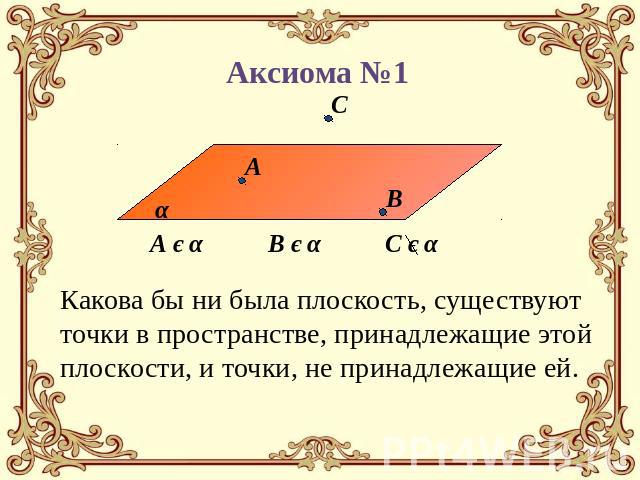
Аксиома №1 Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.

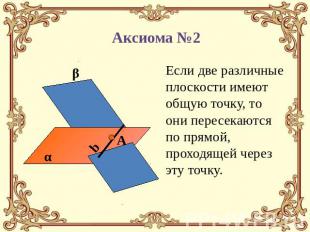
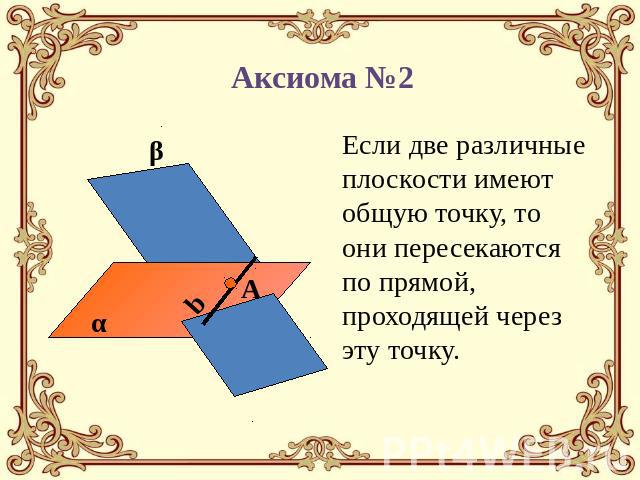
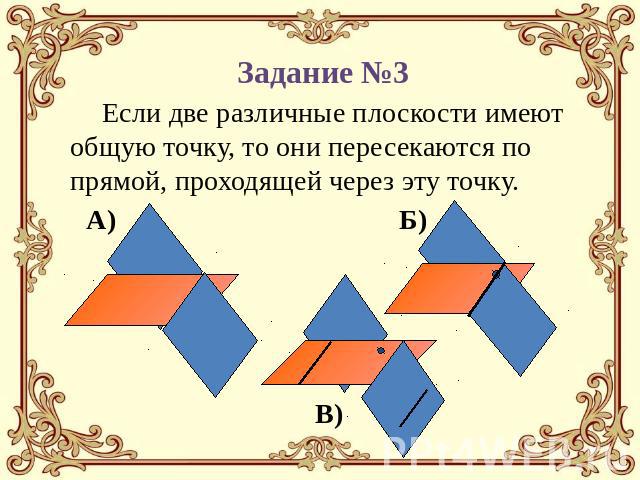
Аксиома №2 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

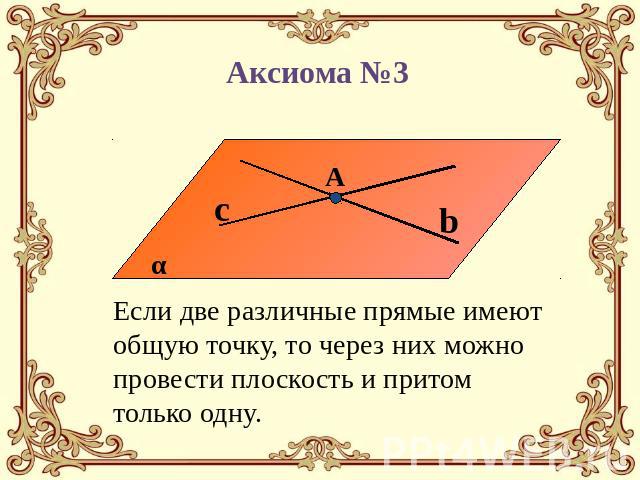
Аксиома №3 Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.

Задание №1 А) Как бы ни было, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.Б) Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.В) Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости.Г) Какова бы ни была плоскость, существуют точки в пространстве, не принадлежащие ей.

А) Если плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.Б) Если две различные плоскости имеют общую точку, то они пересекаются по прямой.В) Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

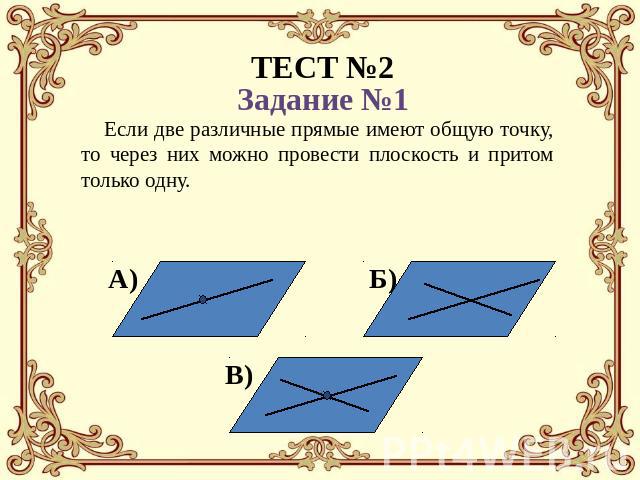
А) Через две прямые можно провести плоскость и притом только одну.Б) Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.В) Если прямые имеют общую точку, то через них можно провести плоскость.

ПРОВЕРЬ СЕБЯОтветы на Тест №1 1 – Б) Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.2 – В) Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.3 – Б) Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.

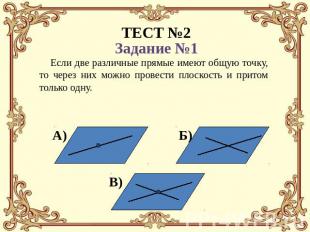
Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.

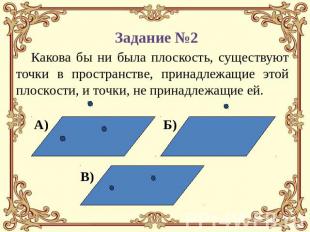
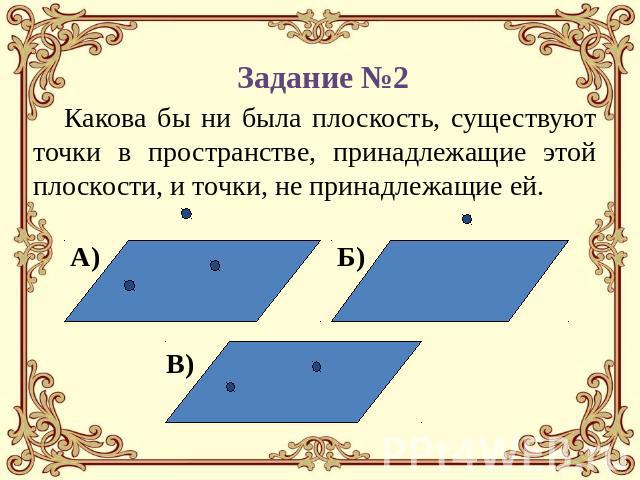
Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.

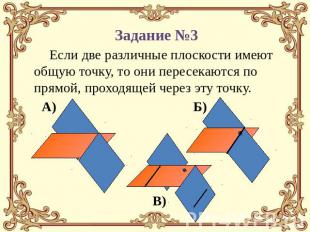
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

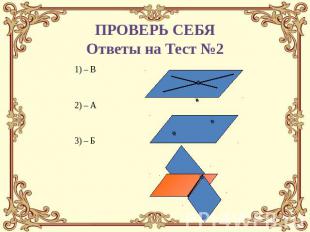
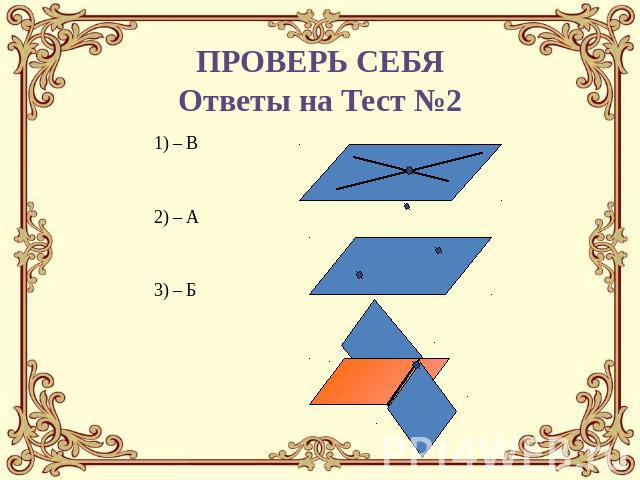
ПРОВЕРЬ СЕБЯОтветы на Тест №21) – В2) – А3) – Б

Практическая работа(Для самопроверки) Группа 1, 4 – задача №1Группа 2, 5 – задача №2Группа 3, 6 – задача №3

Домашнее задание Из задач №1-4 (две обязательные для решения)Третья задача по выбору Составить задачу на применение аксиом (по желанию).

Итог урока

СПАСИБО ЗА ВНИМАНИЕ