Презентация на тему: Особенности геометрических построений на компьютере

Особенности геометрических построений на компьютереАвтор: Виноградов Никита,ученик 9 класса, МКОУ Плесской средней общеобразовательной школы, обучающийся объединения «Программирование» МКОУ ДОД ЦДЮТРуководитель: Юдин Андрей Борисович,учитель математики МКОУ Плесской средней общеобразовательной школы, педагог дополнительного образованияМКОУ ДОД ЦДЮТ 

Выяснить какие знания из курса алгебры и геометрии требуются для решения задач на построение геометрических фигур на компьютере, и разработать алгоритмы для решения задач на построение.

Ознакомится с теорией построений изображений на компьютере при помощи «базовой точки».Найти необходимые формулы для построения геометрических фигур.Реализовать полученные алгоритмы в системе программирования PascalABC.Составить «сборник» использованных мною формул, определений и теорем.

Поисковый метод с использованием научной и учебной литературы. Практический метод составления алгоритмов решения задач, и их реализация в системе программирования PascalABC. Исследовательский метод при выборе алгоритма решения задачи, и построении математической модели. Анализ полученных в ходе исследования данных

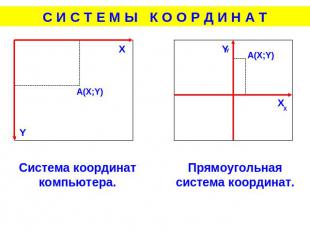
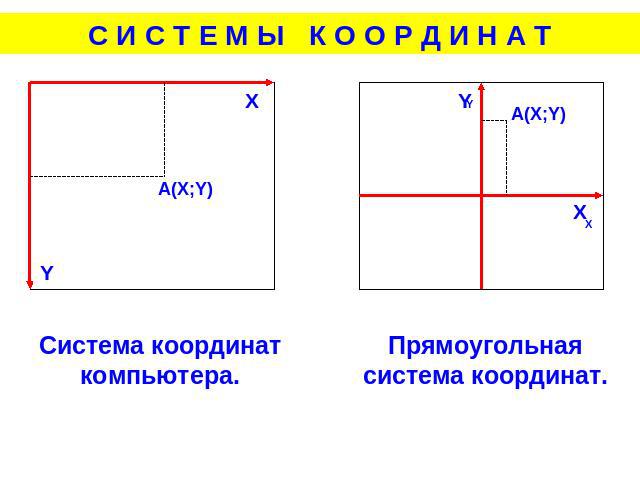
Система координат компьютера.Прямоугольная система координат.

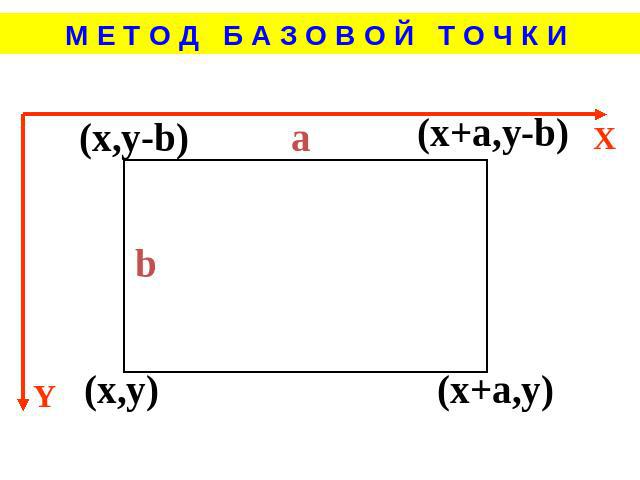
М Е Т О Д Б А З О В О Й Т О Ч К И

Построение прямоугольного треугольника по двум катетам.Построение прямоугольного треугольника по катету и гипотенузе.Построение равностороннего треугольника.Построение треугольника по трем сторонам.Правильный шестиугольникМедиана к основанию и средняя линия треугольника.Построение трапеции по сторонам.Построение параллелограмма по двум сторонам и углу между ними.Построить вписанную в треугольник окружностьПостроить описанную вокруг треугольника окружность.

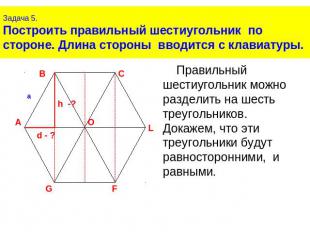
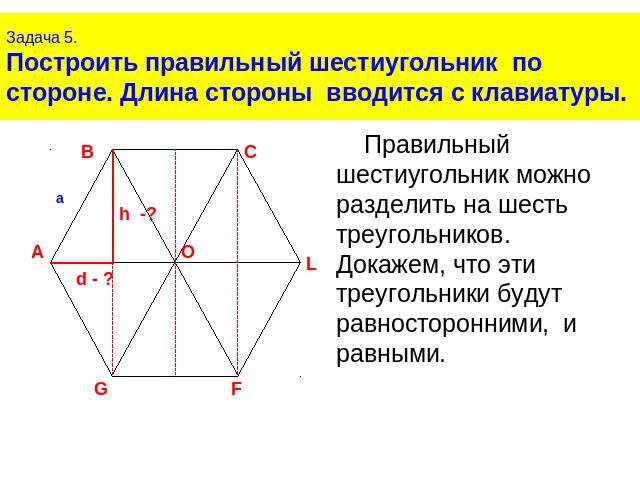
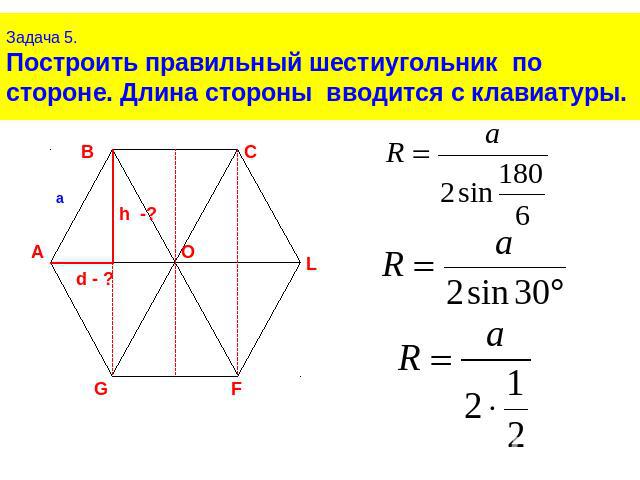
Задача 5.Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры.Правильный шестиугольник можно разделить на шесть треугольников.Докажем, что эти треугольники будут равносторонними, и равными.

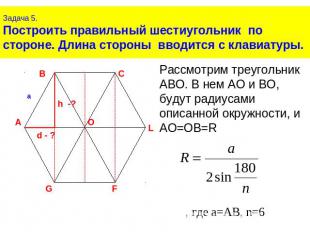
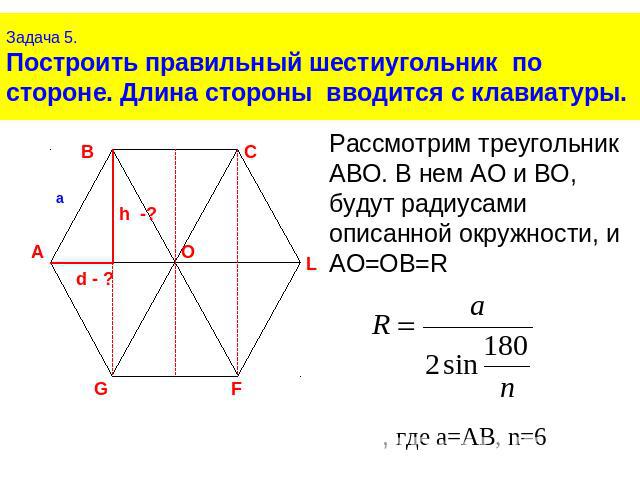
Задача 5.Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры.Рассмотрим треугольник АВО. В нем АО и ВО, будут радиусами описанной окружности, и АО=ОВ=R

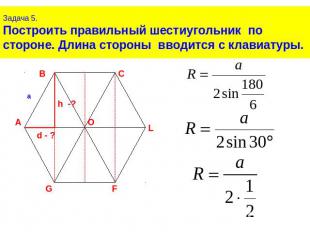
Задача 5.Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры.

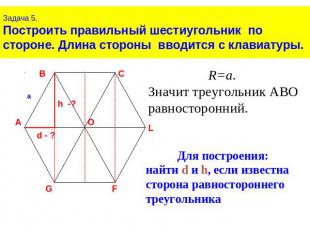
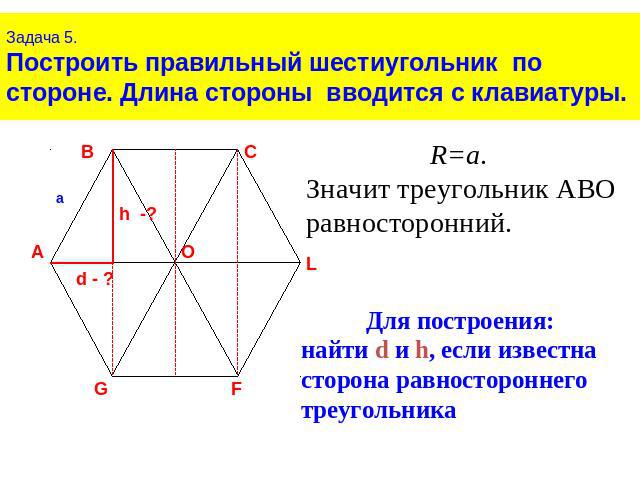
Задача 5.Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры.Значит треугольник АВО равносторонний. Для построения:найти d и h, если известна сторона равностороннего треугольника

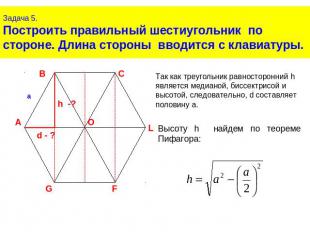
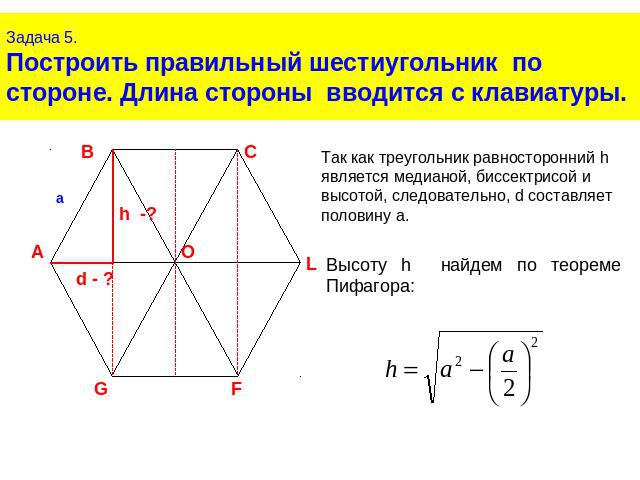
Задача 5.Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры.Так как треугольник равносторонний h является медианой, биссектрисой и высотой, следовательно, d составляет половину a.

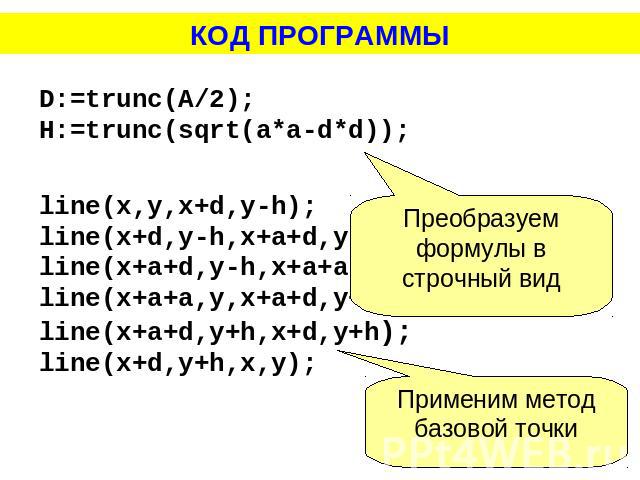
КОД ПРОГРАММЫПреобразуем формулы в строчный видПрименим метод базовой точки

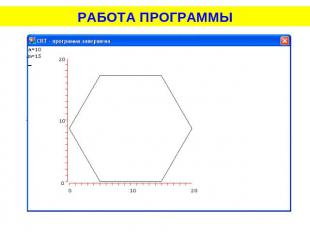
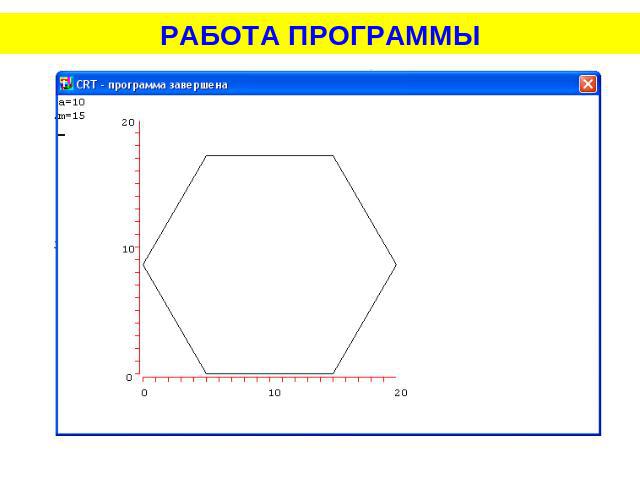
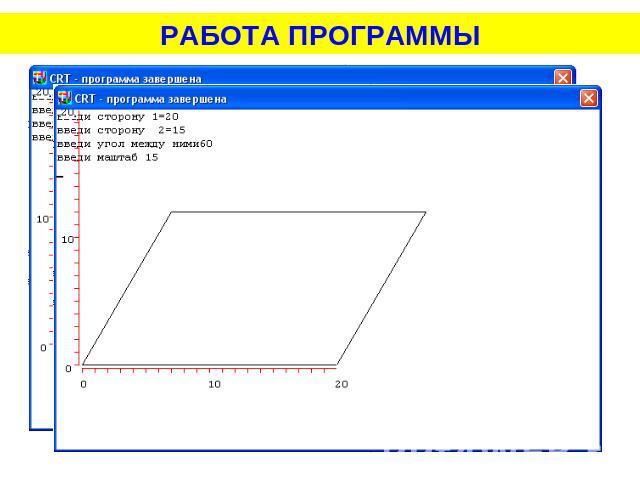
РАБОТА ПРОГРАММЫ

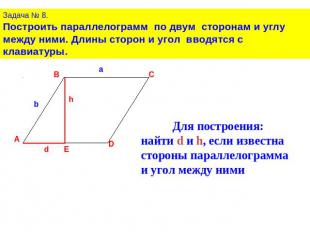
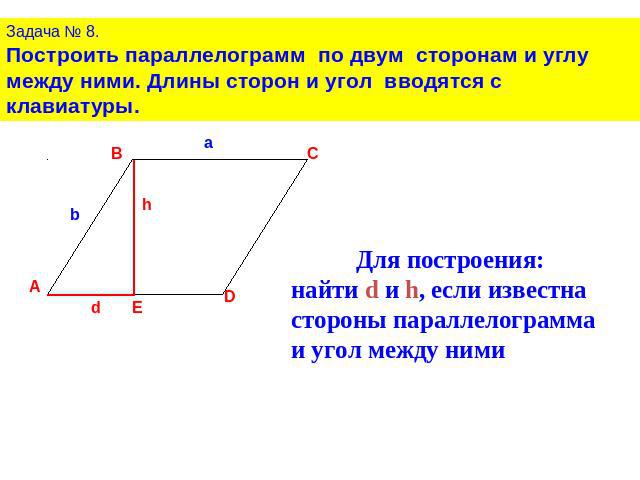
Задача № 8.Построить параллелограмм по двум сторонам и углу между ними. Длины сторон и угол вводятся с клавиатуры.Для построения:найти d и h, если известна стороны параллелограмма и угол между ними

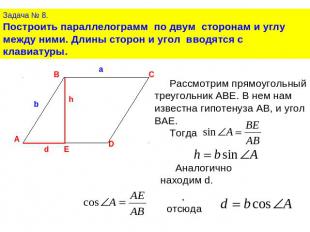
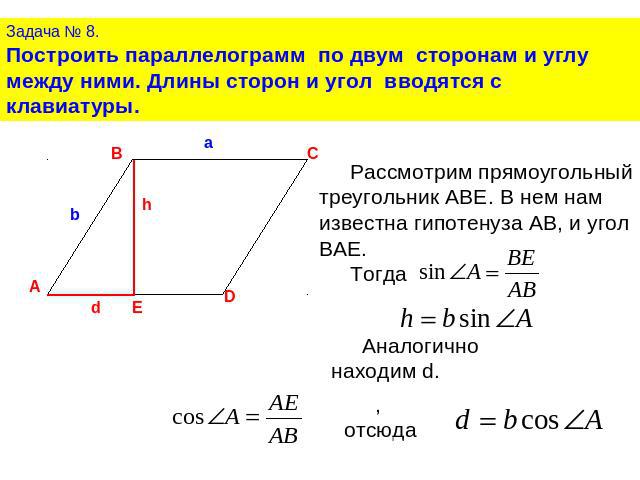
Задача № 8.Построить параллелограмм по двум сторонам и углу между ними. Длины сторон и угол вводятся с клавиатуры.Рассмотрим прямоугольный треугольник ABE. В нем нам известна гипотенуза АВ, и угол BAE. Тогда

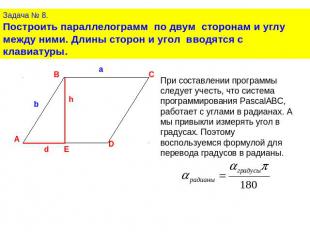
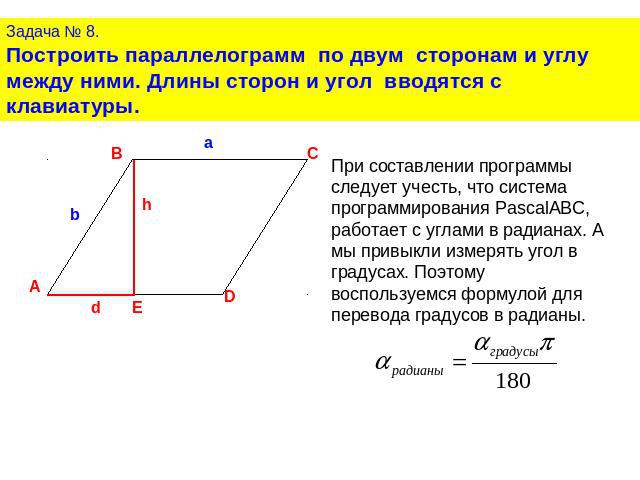
Задача № 8.Построить параллелограмм по двум сторонам и углу между ними. Длины сторон и угол вводятся с клавиатуры.При составлении программы следует учесть, что система программирования PascalABC, работает с углами в радианах. А мы привыкли измерять угол в градусах. Поэтому воспользуемся формулой для перевода градусов в радианы.

Преобразуем формулы в строчный видПрименим метод базовой точки

РАБОТА ПРОГРАММЫ

Для решения этих задач мне потребовались следующие математические знания:Треугольник— это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Три точки, образующие треугольник, называются вершинами треугольника, а отрезки — сторонами треугольника..Треугольник, у которого все стороны равны, называется равносторонним или правильным.Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами Теорема о медиане равнобедренного треугольника. Медиана, проведённая к основанию в равнобедренном треугольнике, является высотой и биссектрисой

Для решения этих задач мне потребовались следующие математические знания:Окружность называется описанной около треугольника, если она проходит через все его вершины. Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середину этих сторон Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, т.е. лежат на параллельных прямых. Противоположные стороны параллелограмма попарно равны.Теорема Пифагора. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Синус угла - это отношение длины противоположного этому углу катета к гипотенузеКосинус угла - это отношение прилежащего этому углу катета к гипотенузе

Для решения этих задач мне потребовались следующие математические знания:Формула для перевода градусов в радианы Радиус окружности описанной вокруг правильного n угольника. … а для остальных задач, еще 31 правило и определение!

Проанализировав решенные мною задачи, я выписал те теоремы, определения и формулы из курса алгебры и геометрии 8 и 9 классов, которые были использованы при составлении этих 10 программ. Сами программы очень простые. В них реализован линейный алгоритм. Вся трудность заключалась в выводах формул, при помощи которых компьютер вычислял необходимые данные для построения геометрических фигур.

Программирование компьютерной графики невозможно без знания математики. Для построения геометрических фигур используется специальный метод, «базовой точки».

Александра Чигринец, на одном из форумов посвященных программированию сказал «…кроме того, математика формирует определённый склад мышления. Какой-то класс задач можно кодить без математики. Но в школе и институте закладывается база, фундамент. Чем фундамент основательнее, тем больше есть возможностей по возведению на нём чего-либо в будущем.Как говорил Абдула в "Белом солнце пустыни": "Хорошо тому, у кого есть кинжал. И плохо если его не окажется… в нужное время." Так вот запасаться кинжалом нужно заранее, а когда он понадобиться, то надо будет достать и пользоваться.»