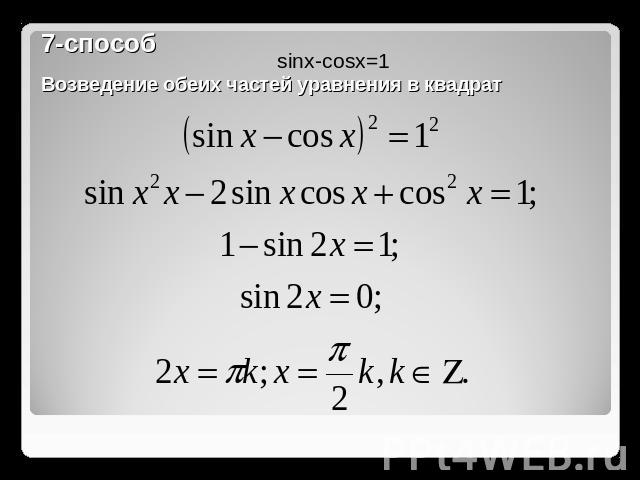Презентация на тему: 7 способов решения тригонометрического уравнения

способов решения тригонометрического уравненияили еще раз о sin x – cos x=1красоте математики. Авторы проекта: Шишкина Диана Диденко Инна10 класс

Проблема красоты привлекала и привлекаетвеличайшие умы человечества. Математики видят ее в: гармонии чисел и форм, геометрической выразительности,стройности математических формул,решении задач различными способами,изяществе математических доказательств,порядке,богатстве приложений универсальных математических методов.

Но красота математики выражается не только в красоте форм ,наглядной выразительности математических объектов, восприятие которых сопряжено с наименьшими усилиями.Ее привлекательность будет усиливаться за счет эмоционально-экпрессивной составляющей - оригинальности, неожиданности, изящества.Математики живут ради тех славных моментов,когда проблема оказывается решенной,ради моментовозарения, восторга

Можно ли насладиться решением уравнения sinx-cosx=1?Да, если стать его исследователем!

Универсальные методы решения уравненияsin x – cos x=1 Мы уже говорили о богатстве приложений универсальных математических методов. При решении уравнений одним из них является метод разложения на множители.Можно ли применить его к решению уравненияSin x –cos x = 1?На первый взгляд,кажется что нет…А если использовать специфические тригонометрические преобразования

Рассуждаем Преобразуем исходное уравнениеSin x – cos x = 1 к видуSin x – ( 1 + cos x) = 0.Мы не просто в правой части уравнения получили ноль,мы выделиливыражение 1 + cos x …Как вы думаете зачем

Ну, конечно,вы догадались ! Необходимо перейти к половинному аргументу,применив формулу повышения степении формулу двойного аргументаИтак…

Разложение левой части уравнения на множители sinx-cosx=1

Произведение равно нулю, если хотя бы один из множителей равен нулю, а остальные при этом не теряют смысла, поэтомуоднородное уравнение первой степени.

Делим обе его части на что противоречит тождеству Получим Ответ:

Приведение уравнения к однородному относительно синуса и косинуса sinx-cosx=1Разложим левую часть по формулам двойногоаргумента, а правую часть заменимтригонометрической единицей:И так далее, как в предыдущем способе …

Тригонометрия удивительна тем ,что она даёт собственные оригинальные способы преобразования разности (или суммы) тригонометрических функций в произведение:Но увы, в левой части уравнения, мы видим разноименные функции. Как изменить название функции на «кофункцию» ?Есть изящный способ!!! Всего лишь нужно применить формулу приведения!

3-й способ: Преобразование разности ( или суммы) тригонометрических функций в произведение. sinx-cosx=1Запишем уравнение в виде: Применяя формулу разности двух синусов, получимОтвет:

4-й способ Приведение к квадратному уравнению относительно одной из функций Так какВозведем обе части полученного уравнения в квадрат

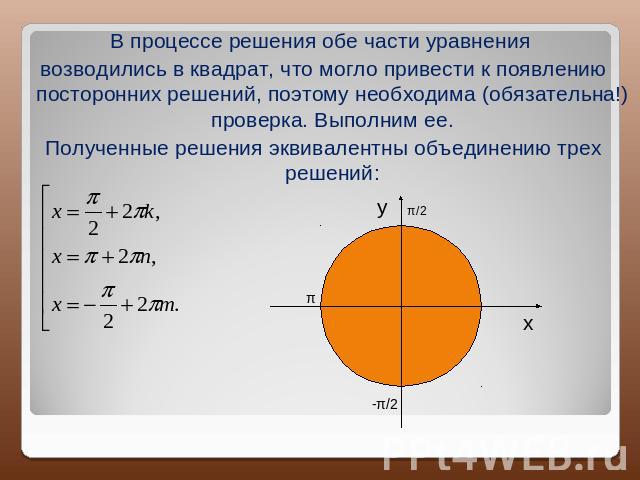
В процессе решения обе части уравнения возводились в квадрат, что могло привести к появлению посторонних решений, поэтому необходима (обязательна!) проверка. Выполним ее.Полученные решения эквивалентны объединению трех решений:

Первое и второе решения совпадают с ранее полученными, поэтому не являются посторонними.Проверим Левая часть:Правая часть:1.Следовательно,

5-й способ Выражение всех функций через tgx (универсальная подстановка) по формулам: С учетом приведенных формул уравнениеsinx-cosx=1запишем в виде

Умножим обе части уравнения на ОДЗ первоначального уравнения – все множество R.

При переходе к из рассмотрения выпали значения, при которыхне имеет смысла, т.е. Следует проверить, не является ли х=π+2πk решением данного уравнения.Левая часть:sin(π+2πk)-cos(π+2πk)=sinπ-cosπ=0-(-1)=1.Правая часть: 1.Значит, х=π+2πk, k€Z – решение уравнения.Ответ:

На ряду с универсальными методами решения уравнений, есть и специфические. Наиболее ярким из них является метод введения вспомогательного угла (числа).Благодаря этому приёму исходное уравнение легко сводится к простейшему –Последний метод, предлагаемый нами, связан также с нестандартным преобразованием тригонометрического уравнения – возведением обеих частей в квадрат. И хотя он является коварным в плане приобретения посторонних корней, но подкупает своим оригинальным способом сведения исходного уравнения к простейшему!просто и красиво!

6-й способВведение вспомогательного угла (числа) sinx-cosx=1В левой части вынесем за скобку ( корень квадратный из суммы квадратов коэффициентов при sinx и cosx). Получим Ответ:

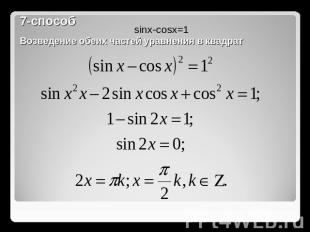
7-способВозведение обеих частей уравнения в квадрат

Полученное решение эквивалентно объединению четырех решений:Проверка показывает, что первое и четвертое решения – посторонние. Ответ:

ВСЁ!Точнее почти всё!Осталось выбрать метод решения, победивший в номинации: Самый простой;Самый оригинальный;Самый неожиданный;Самый универсальный …УДИВИТЕЛЬНОЕ И КРАСИВОЕ ВСЕГДА РЯДОМ!