Презентация на тему: Приёмы устного решения квадратного уравнения

Муниципальное общеобразовательное учреждение «Гимназия №53» Приёмы устного решения квадратного уравнения

Цель: устные приёмы эффективного решения квадратных уравнений.

Алгоритм Извлечения квадратного корня Из натурального числа

Приём «Коэффициентов»: Используя приёмы 1) -3) можно придумывать уравнения с рациональными корнями.

Урок - презентация МОУ «Гимназия №53» Учитель Бойко Т.А.

Квадратные уравнения 8класс

Приобретать знания - храбрость Приумножать их - мудрость А умело применять великое искусство Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных , иррациональных уравнений и неравенств. В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.

Приёмы устного решения квадратного уравнения 1) 2 ) приём «коэффициентов» 3) приём «переброски»

Цели урока: Обобщить и систематизировать изученный материал по теме: «Квадратные уравнения». Научить учащихся приёмам устного решения квадратных уравнений. Развивать внимание и логическое мышление. Воспитывать культуру поведения .

Теоремы

К какому типу относится уравнение

ЗАДАЧА Найти наиболее рациональным способом корни уравнения

Свойства коэффициентов квадратного уравнения Доказательство. Разделим обе части уравнения на получим приведённое квадратное уравнение

Приёмы устного решения решения квадратных уравнений

Решить уравнение

Квадратные уравнения с большими коэффициентами

Приём "переброски"

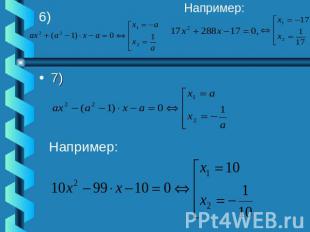
Уравнения с рациональными корнями Используя приёмы решения 1) – 3),вы можете придумывать уравнения с рациональными корнями. Например, возьмём уравнение

Это интересно

Задание Найти №№ 505 – 573 -------------------------------- квадратные уравнения, которые можно решить устно, используя изученные приёмы.

Выводы: данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики; овладение данными приёмами поможет учащимся экономить время и эффективно решать уравнения; потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов; владение алгоритмом извлечения квадратного корня из натурального числа.