Презентация на тему: Геометрический смысл производной

Геометрический смысл производнойУчитель : Потеряйкина О.Н. МОУ СОШ №68 г.Хабаровск

Готфрид Вильгельм фон Лейбниц Геометрическая интерпретация производной, впервые данная в конце XVII в. Лейбницем, который основываясь на результатах Ферма и некоторых других выводах, значительно полнее своих предшественников решил задачу о построении касательной к кривой в некоторой точке.1646г – 1716г

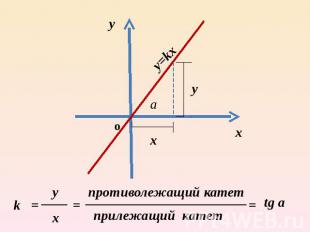
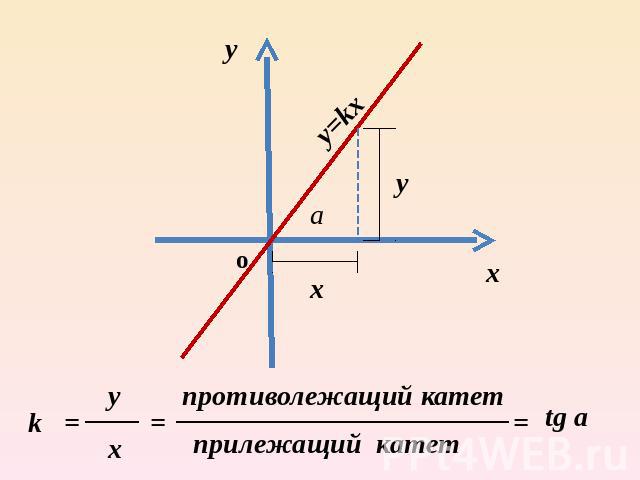
k – угловой коэффициент прямойа –угол между прямой и положительным направлением оси абсцисс

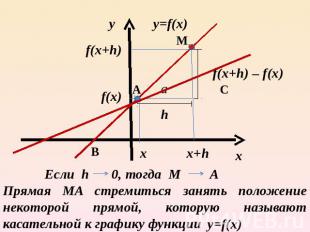
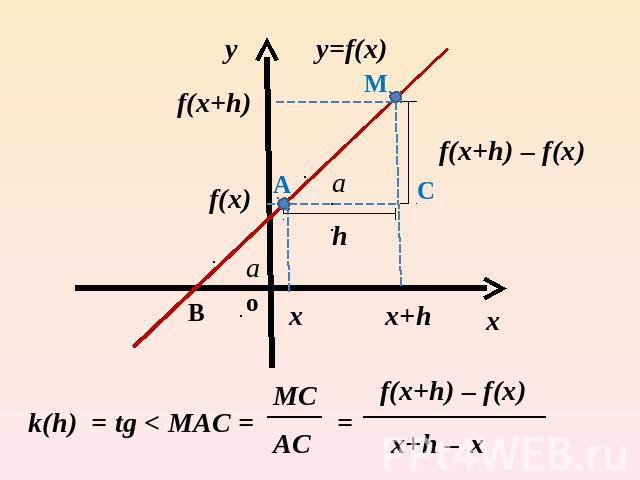
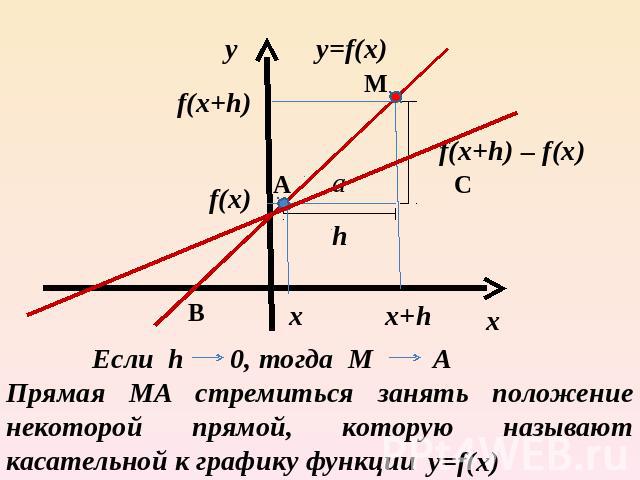
Прямая MA стремиться занять положение некоторой прямой, которую называют касательной к графику функции

Значение производной в точке равно угловому коэффициенту касательной к графику функции в этой точке

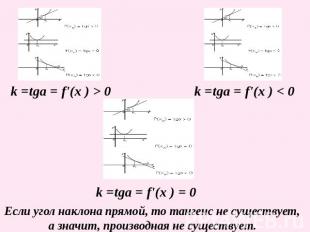
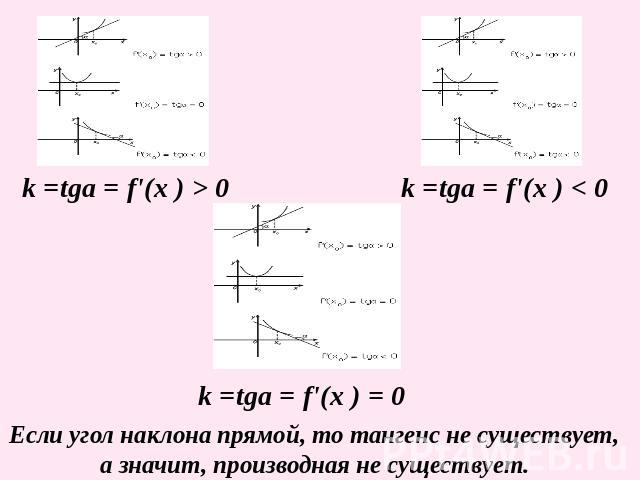
Если угол наклона прямой, то тангенс не существует, а значит, производная не существует.

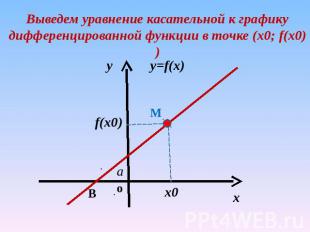
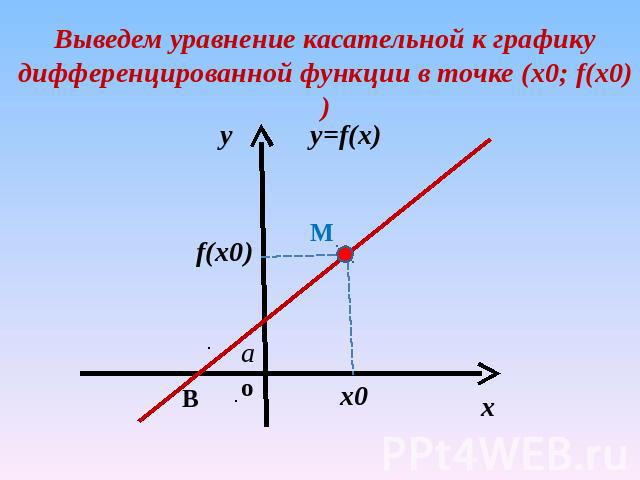
Выведем уравнение касательной к графику дифференцированной функции в точке (х0; f(x0))

Т.к. касательная проходит через точку с координатами (х0; f(x0)) , подставим ее координаты в уравнение (2) и найдем bПодставьте в уравнение (2) значение b и сделав соответствующие преобразования получите:

Алгоритм нахождения уравнения касательной к графику функции y=f(x) в точке с абсциссой х0 f(x0) – находим значение функции в данной точке f '(x) – находим производную данной функцииf'(x0) - находим значение производной функции в данной точкеПодставляем данные в уравнение касательной к графику функции