Презентация на тему: Объём пирамиды

Объём пирамиды. Геометрия, 11 класс.
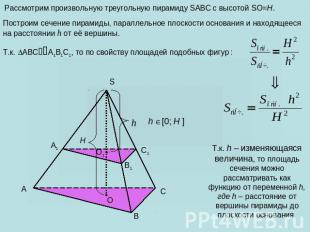
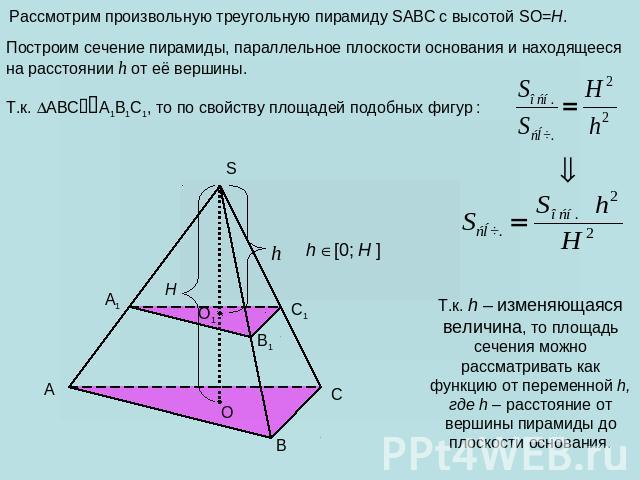
Рассмотрим произвольную треугольную пирамиду SABC с высотой SO=H. Построим сечение пирамиды, параллельное плоскости основания и находящееся на расстоянии h от её вершины. Т.к. ABCA1B1C1, то по свойству площадей подобных фигур : Т.к. h – изменяющаяся величина, то площадь сечения можно рассматривать как функцию от переменной h, где h – расстояние от вершины пирамиды до плоскости основания.

Используя понятие бесконечной интегральной суммы, объем данной пирамиды можно получить как бесконечную сумму площадей таких сечений, построенных вдоль высоты.
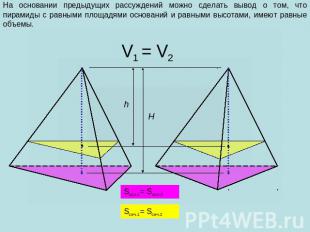
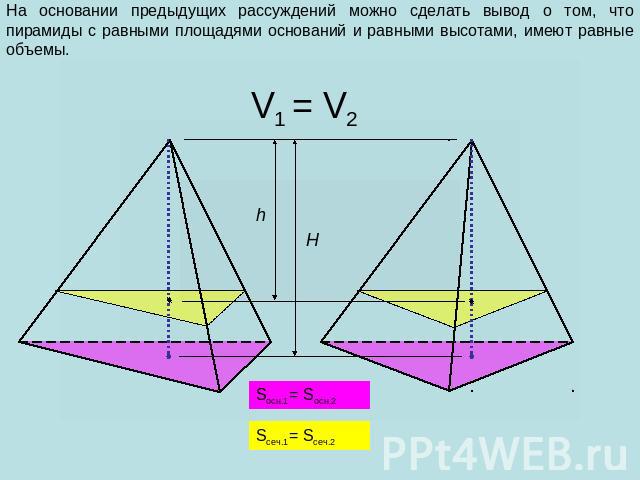
На основании предыдущих рассуждений можно сделать вывод о том, что пирамиды с равными площадями оснований и равными высотами, имеют равные объемы.

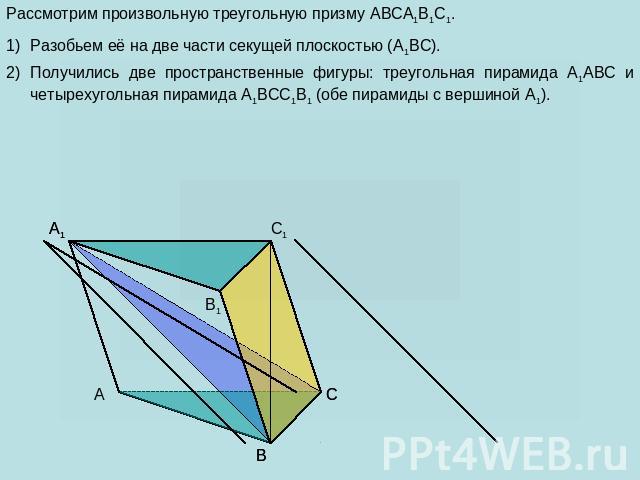
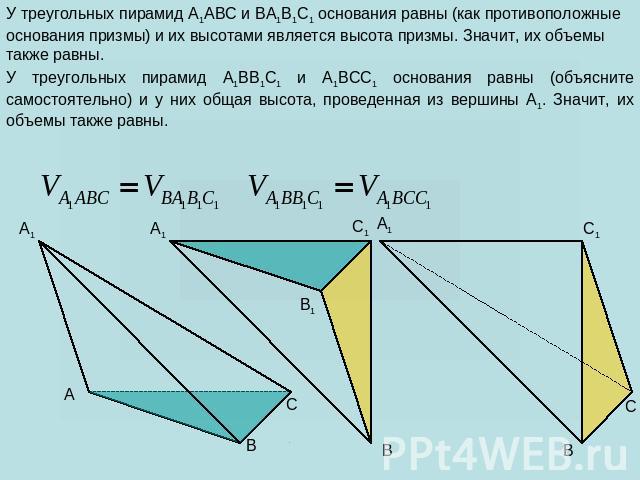
Рассмотрим произвольную треугольную призму ABCA1B1C1. Разобьем её на две части секущей плоскостью (A1BC). Получились две пространственные фигуры: треугольная пирамида A1ABC и четырехугольная пирамида A1BCC1B1 (обе пирамиды с вершиной A1).
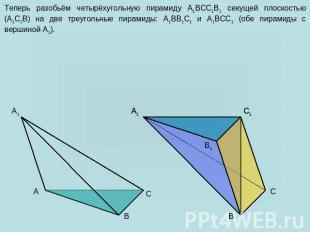
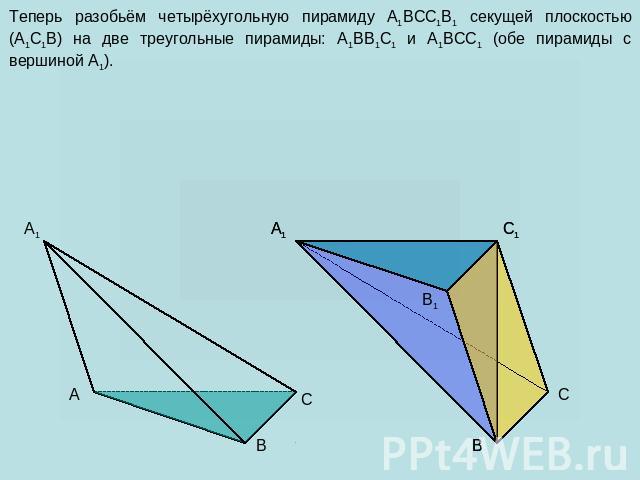
Теперь разобьём четырёхугольную пирамиду A1BCC1B1 секущей плоскостью (A1C1B) на две треугольные пирамиды: A1BB1C1 и A1BCC1 (обе пирамиды с вершиной A1).

У треугольных пирамид A1ABC и BA1B1C1 основания равны (как противоположные основания призмы) и их высотами является высота призмы. Значит, их объемы также равны. У треугольных пирамид A1BB1C1 и A1BCC1 основания равны (объясните самостоятельно) и у них общая высота, проведенная из вершины A1. Значит, их объемы также равны.

Тогда, по свойству транзитивности, объемы всех трех пирамид равны: Значит, объем пирамиды в три раза меньше объема призмы с такими же основанием и высотой, т.е.

Эту же формулу можно было получить непосредственным интегрированием площади сечения, как функции, зависящей от расстояния h:
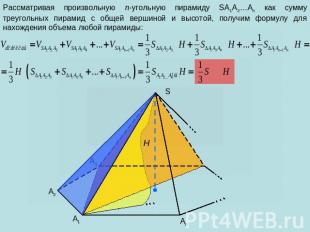
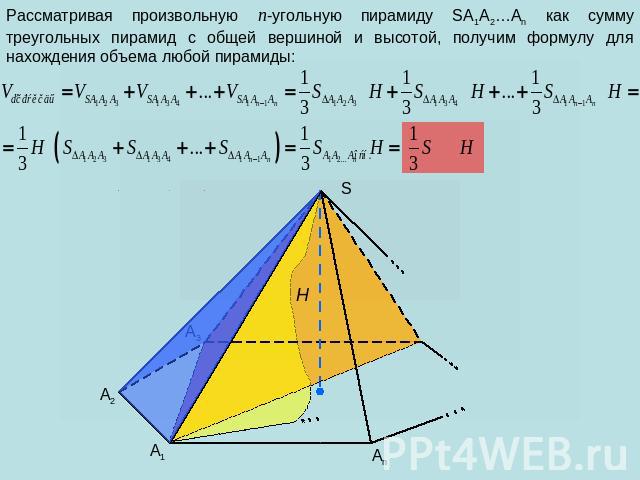
Рассматривая произвольную n-угольную пирамиду SA1A2…An как сумму треугольных пирамид с общей вершиной и высотой, получим формулу для нахождения объема любой пирамиды:

Итак, для любой n-угольной пирамиды: ,где Sосн. – площадь основания пирамиды, H – высота пирамиды.