Презентация на тему: Треугольники 3 класс


Содержание Элементы треугольника Виды треугольников Признаки равенства треугольников - Первый признак - Второй признак - Третий признак Задача Наполеона Софизм равнобедренного треугольника Треугольник Паскаля Теорема синусов и косинусов Вписанная и описанная окружности

виды треугольников Равнобедренный Равносторонний Разносторонний
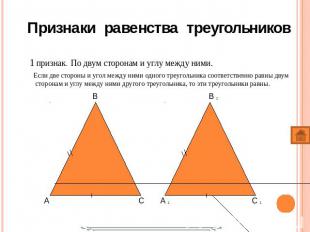
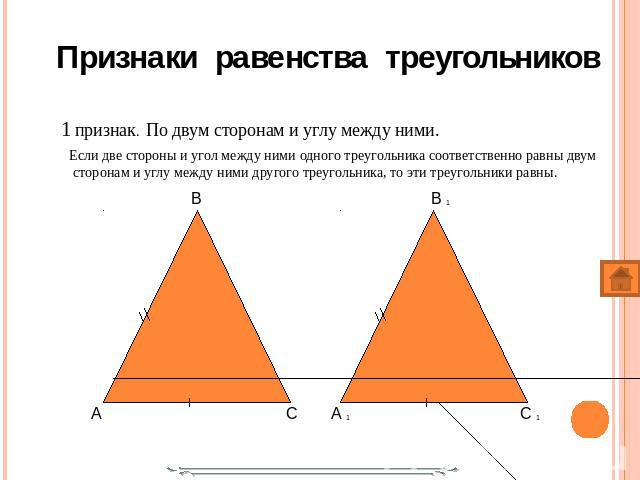
1 признак. По двум сторонам и углу между ними. 1 признак. По двум сторонам и углу между ними. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
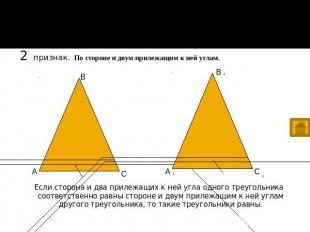
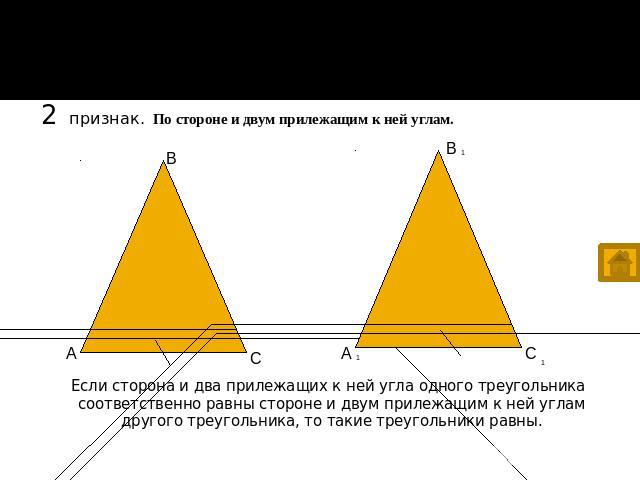
Признаки равенства треугольников 2 признак. По стороне и двум прилежащим к ней углам. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

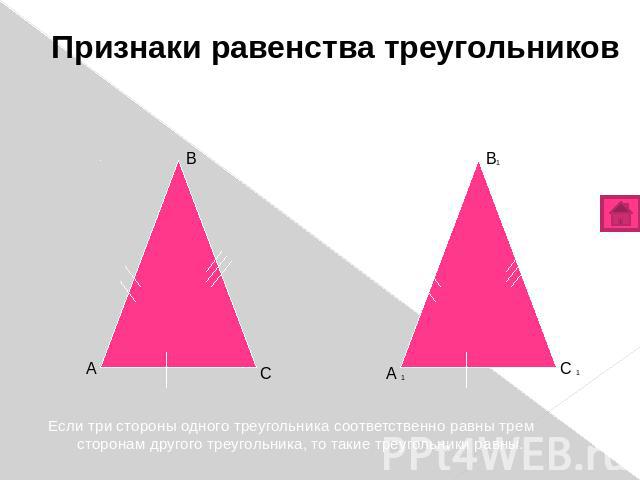
Признаки равенства треугольников 3 признак. По трем сторонам. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
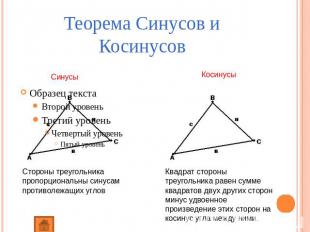
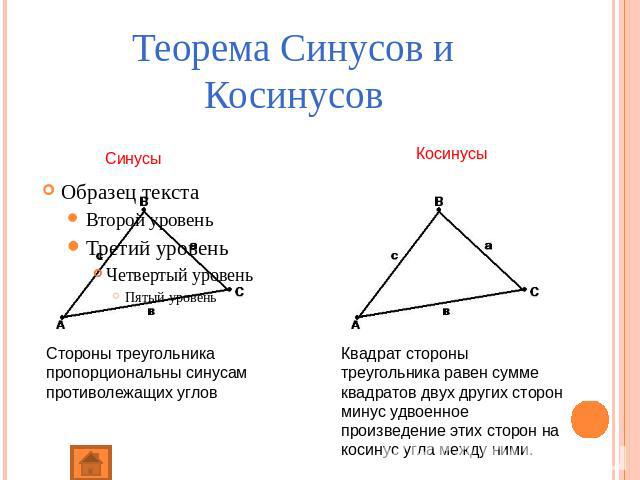
Теорема Синусов и Косинусов Синусы Косинусы Стороны треугольника пропорциональны синусам противолежащих углов Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
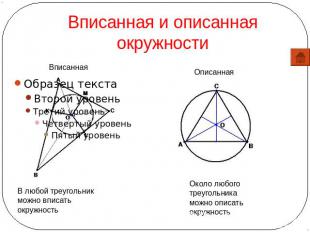
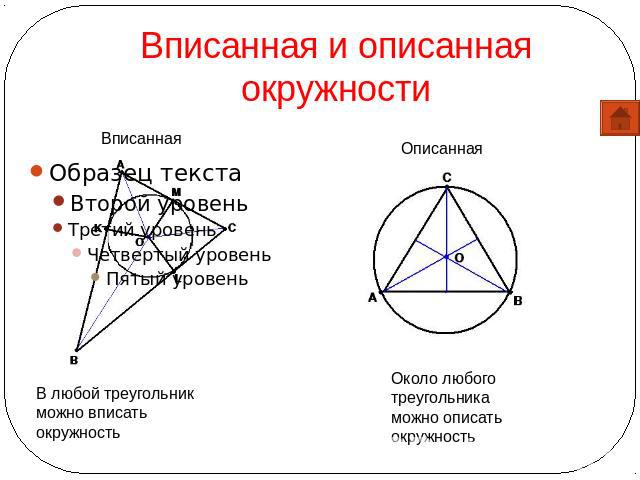
Вписанная и описанная окружности Вписанная В любой треугольник можно вписать окружность Описанная Около любого треугольника можно описать окружность

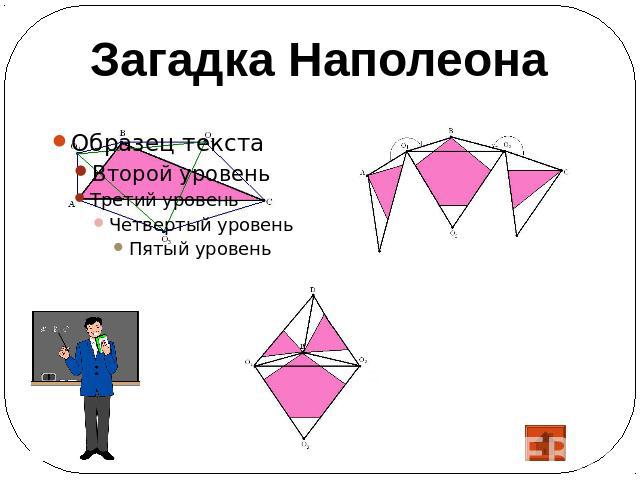
Наполеон Бонапарт Французский император Наполеон Бонапарт был любителем математики. Одно из свидетельств этому – несколько составленных им геометрических задач.
Загадка Наполеона

Софизм равнобедренного треугольника Софизм – доказательство ложного утверждения, причём ошибка в доказательстве искусно замаскирована. Здесь ошибка в чертеже. Серединный перпендикуляр к стороне и биссектриса противоположного ей угла для неравнобедренного треугольника пересекаются вне этого треугольника.

1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 Свойства треугольника Паскаля: 1) В треугольнике Паскаля каждое число кроме крайних единиц равно сумме двух соседних в предыдущей строке. 2) Сумма чисел n-ой строки равна 2n, где n принадлежит целым чис- лам. 3) Сумма чисел любой строки в два раза больше суммы чисел в пре- дыдущей сроке. 4) Числа, равноудаленные от концов любой строки равны между собой. Сmn=Cmm-n