Презентация на тему: Треугольники

Подготовка к ГИА по геометрии Треугольники

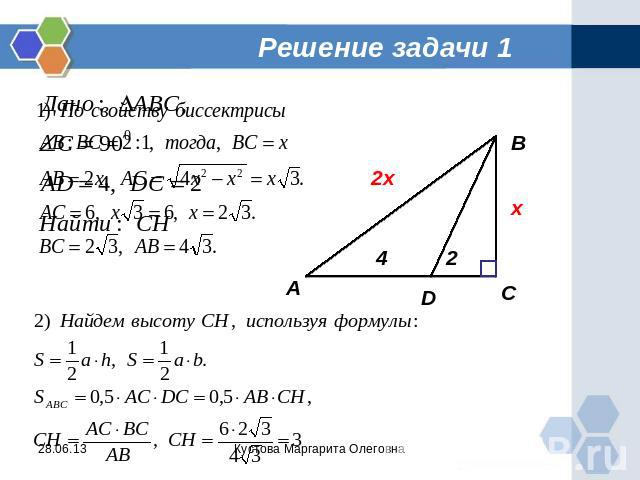
Задача 1 Найдите высоту прямоугольного треугольника, проведенную к гипотенузе, если биссектриса острого угла делит катет на отрезки, равные 2 и 4.
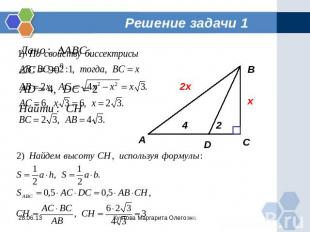
Решение задачи 1

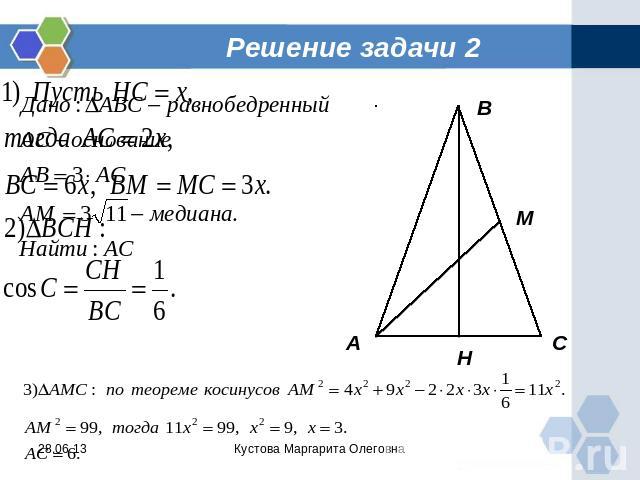
Задача 2 Найдите основание равнобедренного треугольника, если оно в 3 раза меньше боковой стороны, а медиана, проведенная к боковой стороне, равна
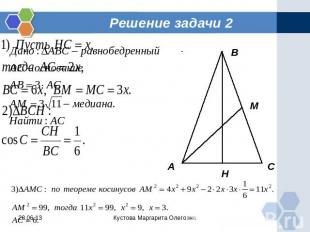
Решение задачи 2

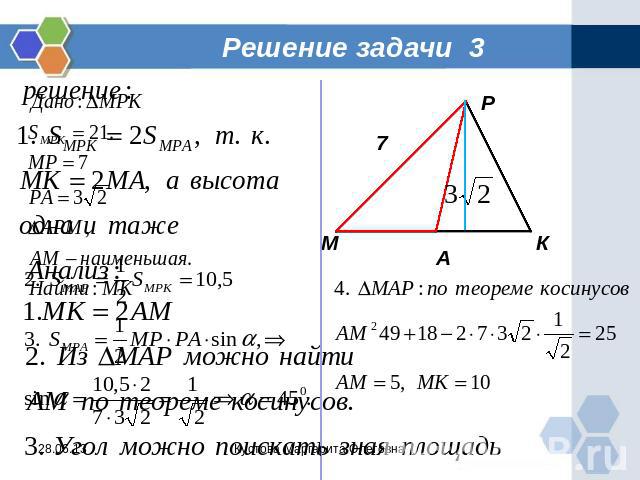
Задача 3 Площадь треугольника МРК равна 21. Известно, что сторона МР равна 7,медиана РА равна 3√2, а в треугольнике АМР сторона АМ – наименьшая. Найдите сторону МК
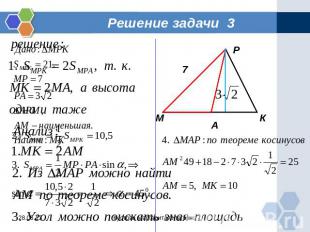
Решение задачи 3

Задача 4 В прямоугольном треугольнике АВС с прямым углом С биссектриса АD делит катет ВС на отрезки BD=15 и DC = 12. Найдите площадь треугольника ABD.

Решение задачи 4

Задача 5 Найдите площадь остроугольного треугольника АВС, если известно, что угол ВАС равен 45°, АВ=4√2, а медиана АМ = √29.

Решение задачи 5