Презентация на тему: Треугольники

УРОК по теме «ТРЕУГОЛЬНИКИ» “Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг геометрия” французский архитектор Ле Корбюзье

Треугольник Треугольник – это геометрическая фигура, состоящая из трёх точек плоскости, не лежащих на одной прямой и трех отрезков попарно соединяющих эти точки.

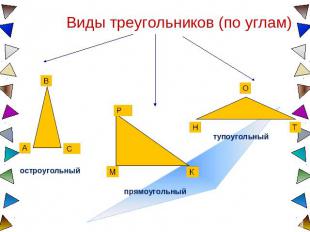
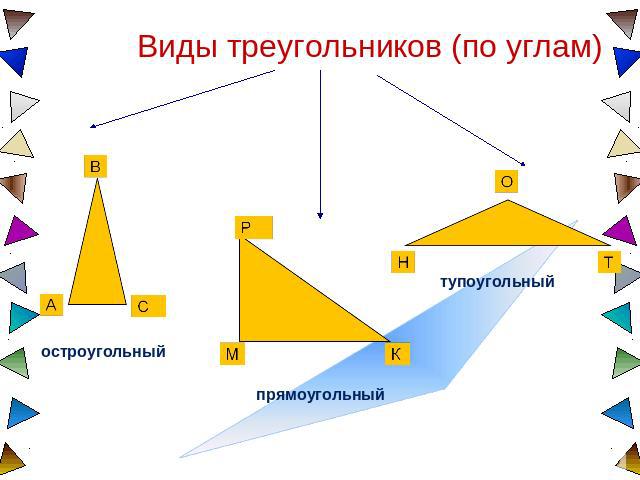
Виды треугольников (по углам)

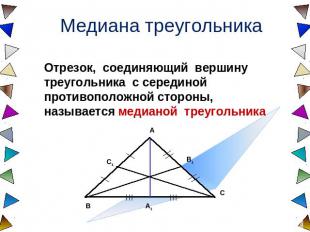
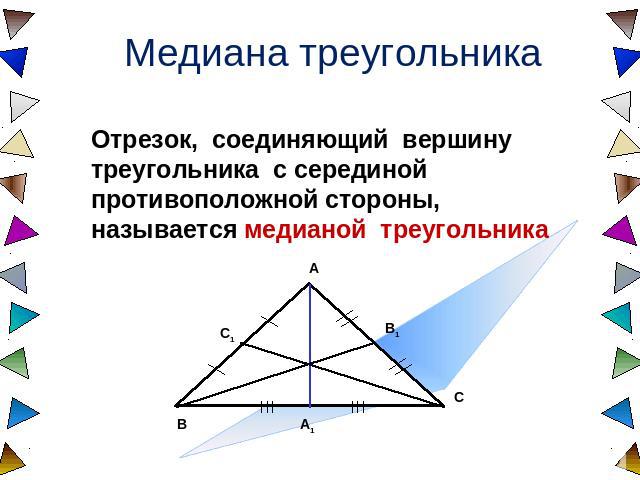
Медиана треугольника Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника

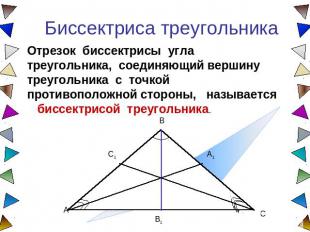
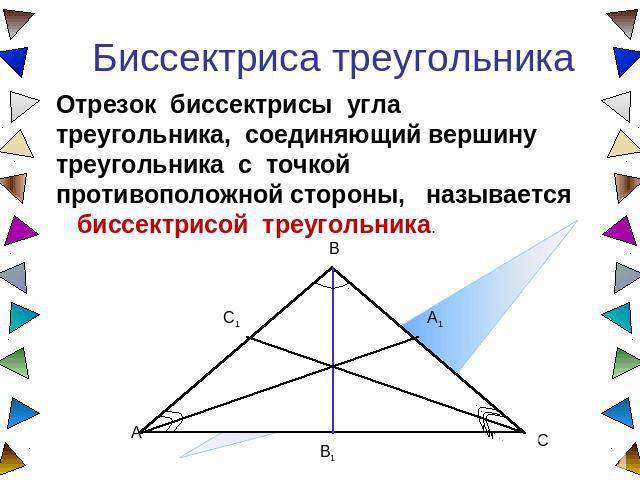
Биссектриса треугольника Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

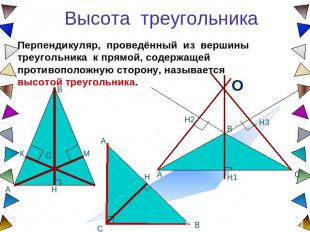
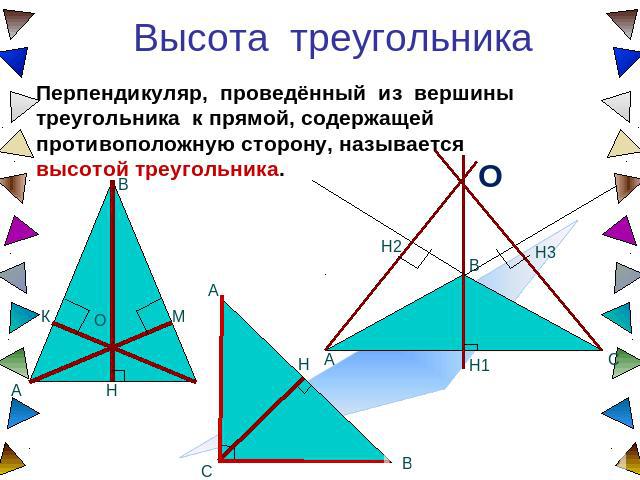
Высота треугольника Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

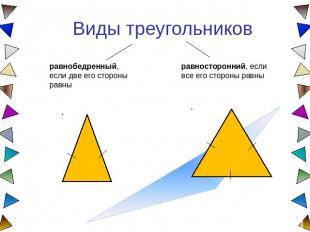
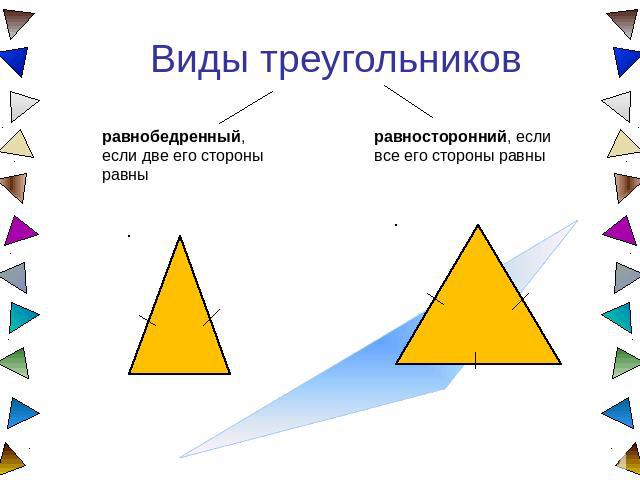
Виды треугольников равнобедренный, если две его стороны равны равносторонний, если все его стороны равны

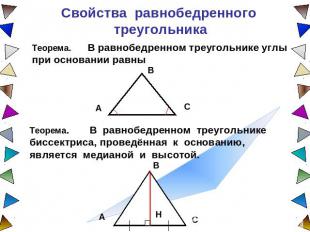
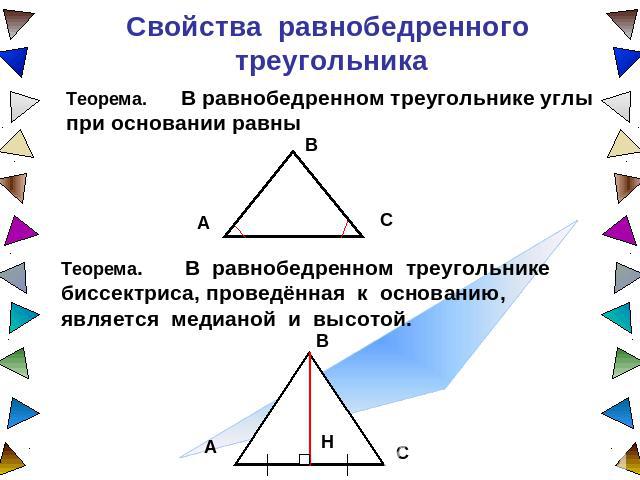
Свойства равнобедренного треугольника Теорема. В равнобедренном треугольнике углы при основании равныТеорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

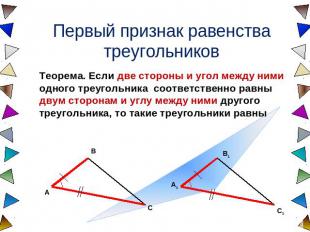
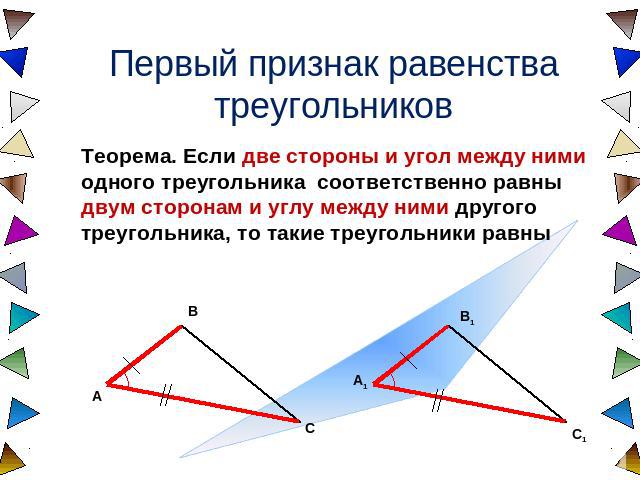
Первый признак равенства треугольников Теорема. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны

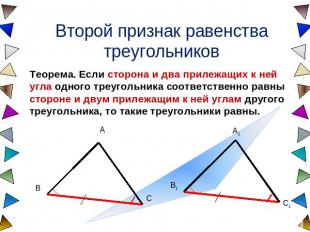
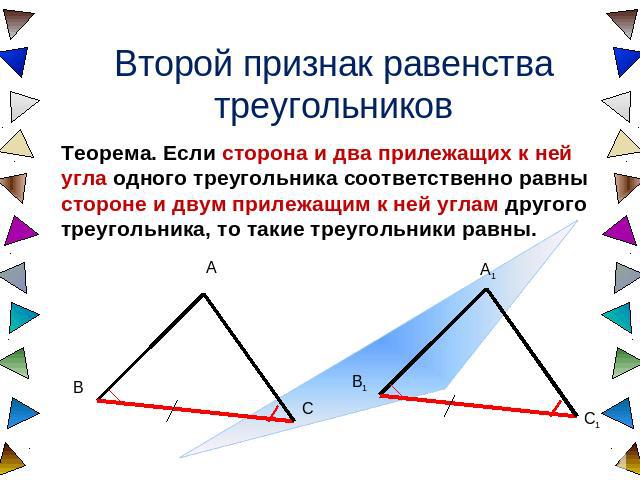
Второй признак равенства треугольников Теорема. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

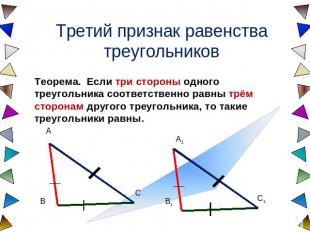
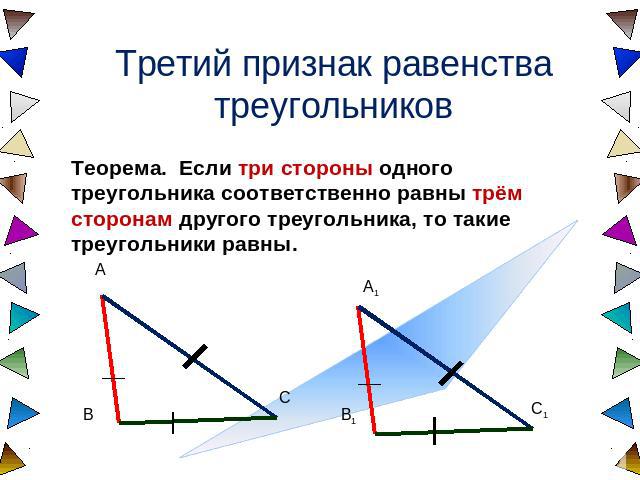
Третий признак равенства треугольников Теорема. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Олимпийский флаг

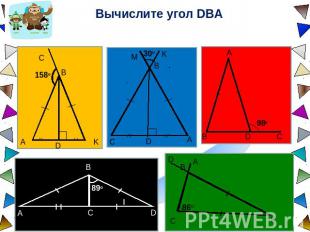
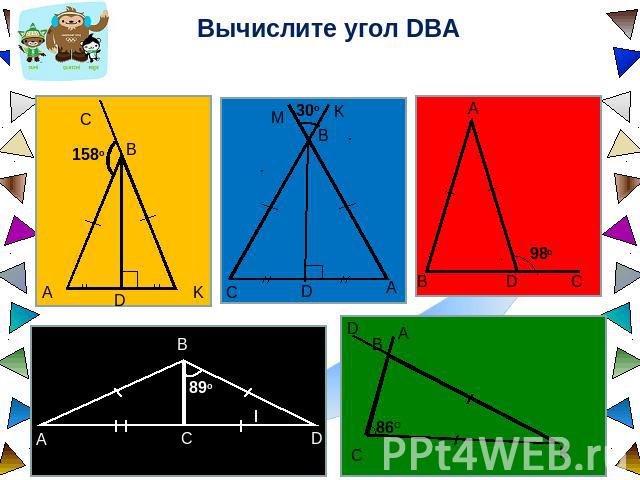
Вычислите угол DBA

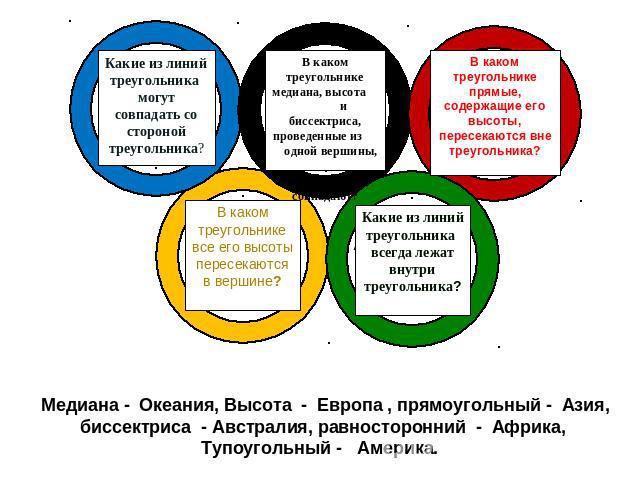
Олимпийский флаг

Медиана - Океания, Высота - Европа , прямоугольный - Азия,биссектриса - Австралия, равносторонний - Африка, Тупоугольный - Америка.

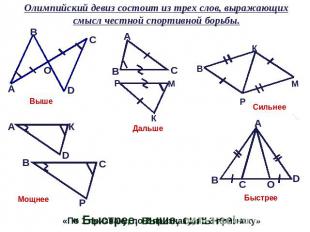
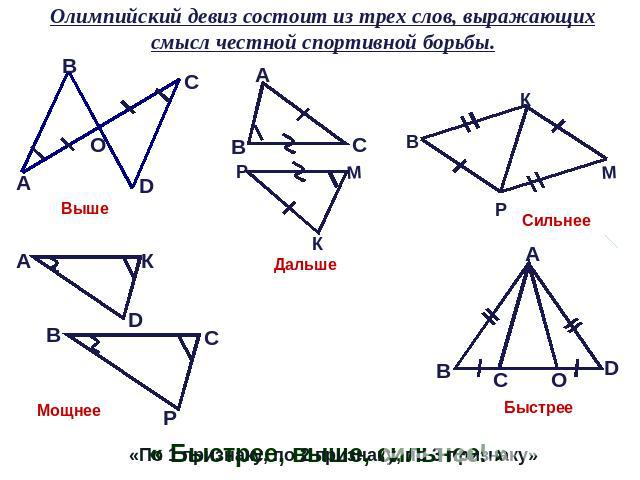
Олимпийский девиз состоит из трех слов, выражающих смысл честной спортивной борьбы.

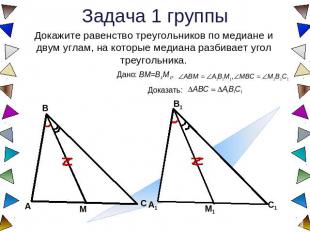
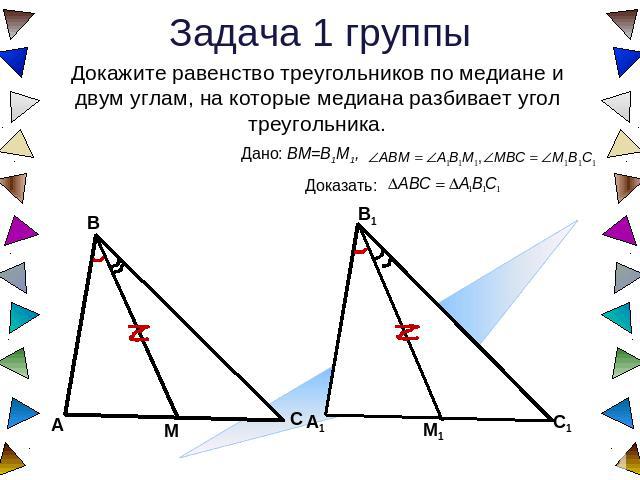
Задача 1 группы Докажите равенство треугольников по медиане и двум углам, на которые медиана разбивает угол треугольника.

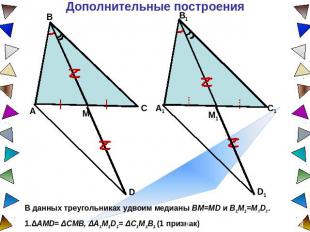
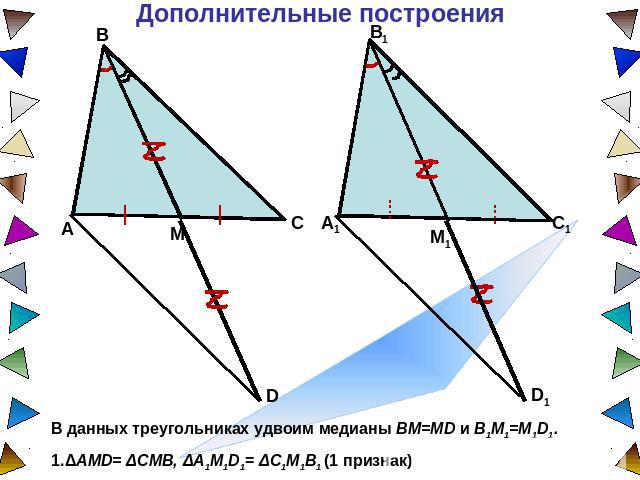
Дополнительные построения В данных треугольниках удвоим медианы BM=MD и B1M1=M1D1. 1.ΔAMD= ΔCMB, ΔA1M1D1= ΔC1M1B1 (1 признак)

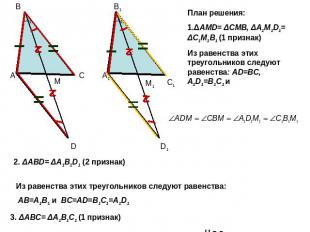
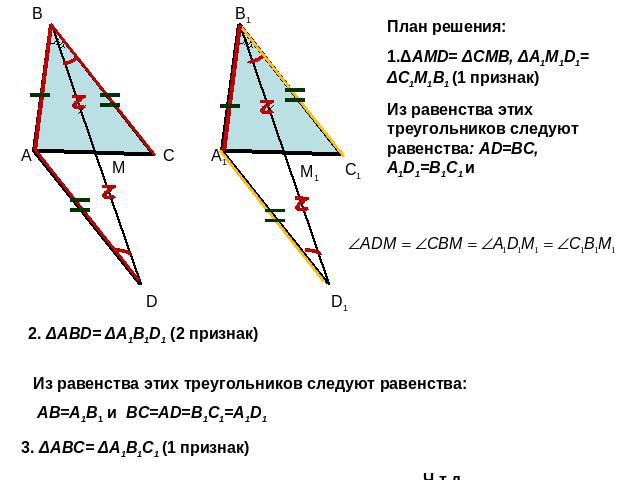
План решения: 1.ΔAMD= ΔCMB, ΔA1M1D1= ΔC1M1B1 (1 признак)Из равенства этих треугольников следуют равенства: AD=BC, A1D1=B1C1 и2. ΔABD= ΔA1B1D1 (2 признак)Из равенства этих треугольников следуют равенства: AB=A1B1 и BC=AD=B1C1=A1D13. ΔABC= ΔA1B1C1 (1 признак)Ч.т.д.

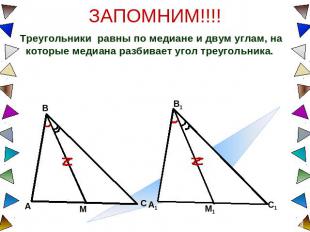
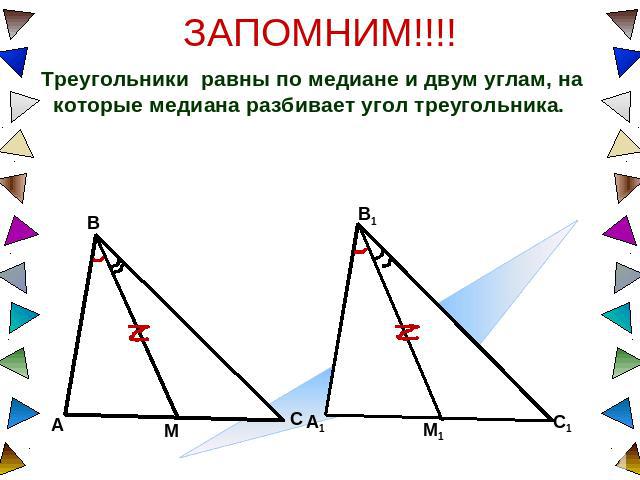
ЗАПОМНИМ!!!! Треугольники равны по медиане и двум углам, на которые медиана разбивает угол треугольника.

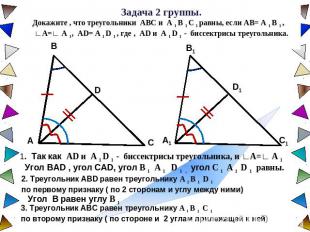
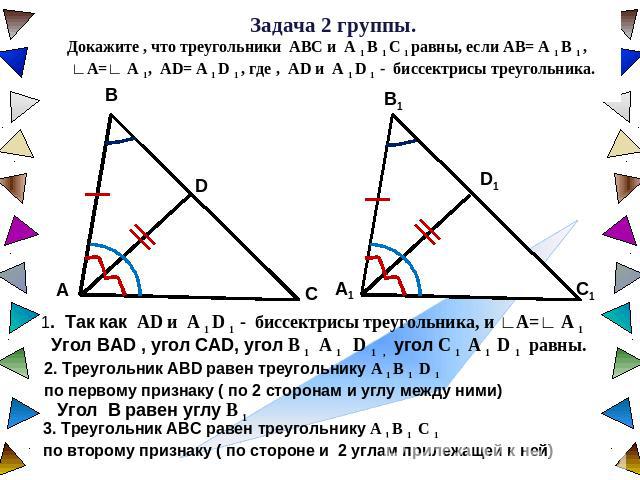
Задача 2 группы. Докажите , что треугольники ABC и A 1 B 1 C 1 равны, если AB= A 1 B 1 , ∟А=∟ A 1, AD= A 1 D 1 , где , AD и A 1 D 1 - биссектрисы треугольника. 1. Так как AD и A 1 D 1 - биссектрисы треугольника, и ∟А=∟ A 1 2. Треугольник ABD равен треугольнику A 1 B 1 D 1 по первому признаку ( по 2 сторонам и углу между ними)3. Треугольник ABС равен треугольнику A 1 B 1 С 1 по второму признаку ( по стороне и 2 углам прилежащей к ней)

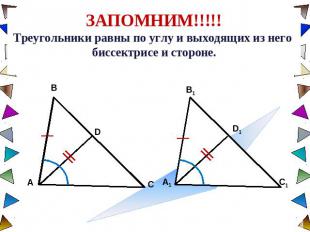
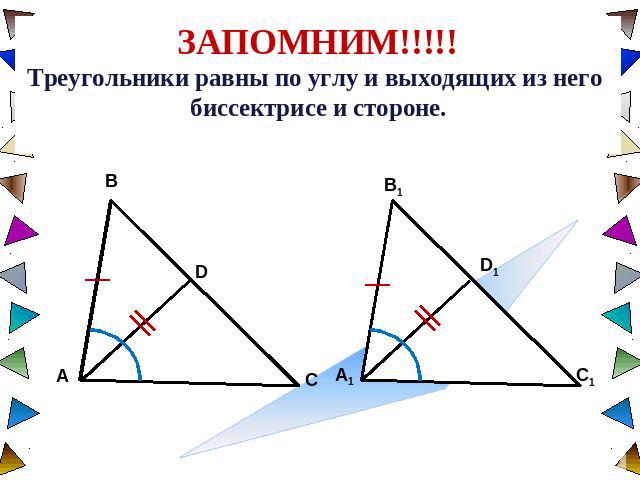
ЗАПОМНИМ!!!!!Треугольники равны по углу и выходящих из него биссектрисе и стороне.

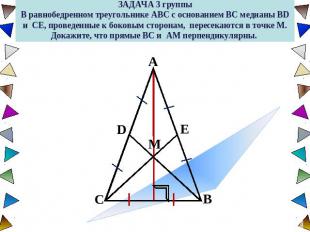
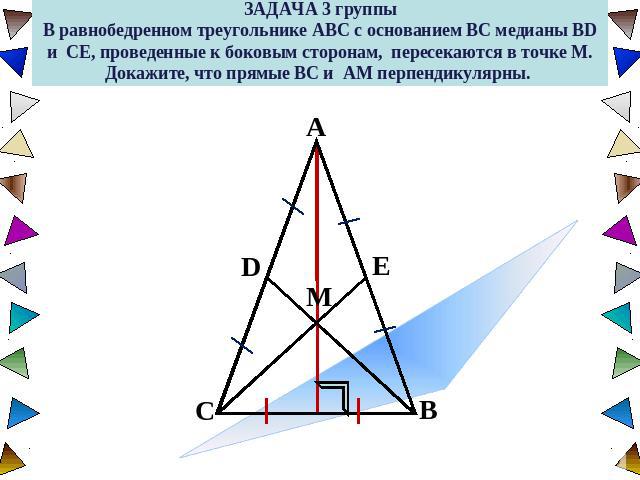
ЗАДАЧА 3 группыВ равнобедренном треугольнике ABC с основанием BC медианы BD и CE, проведенные к боковым сторонам, пересекаются в точке M. Докажите, что прямые BC и AM перпендикулярны.