Презентация на тему: Аксиома параллельных прямых

«Аксиома параллельныхпрямых»

«Геометрия полна приключений,потому что за каждой задачей скрывается приключение мысли.Решить задачу – это значит пережить приключение».(В. Произволов)

Закончи предложение.Прямая х называется секущей по отношению к прямым а и b, если…2. При пересечении двух прямых секущей образуется … неразвёрнутых углов.3. Если прямые АВ и СD пересечены прямой ВD, то прямая ВD называется…4. Если точки В и D лежат в разных полуплоскостях относительно секущей АС,то углы ВАС и DCA называются…5. Если точки В и D лежат в одной полуплоскости относительно секущей АС, тоуглы ВАС и DCA называются…6. Если внутренние накрест лежащие углы одной пары равны, то внутренниенакрест лежащие углы другой пары…

Проверка задания.1.…если она пересекает их в двух точках2. 83.…секущей4.…накрест лежащими5.…односторонними6.…равны
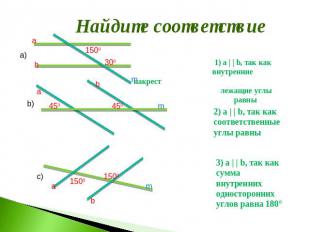
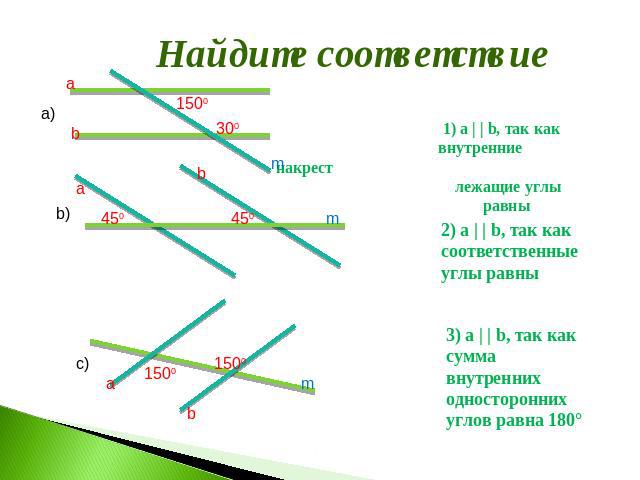
Найдите соответствие 1) a | | b, так как внутренние накрест лежащие углы равны 2) a | | b, так каксоответственныеуглы равны 3) a | | b, так каксумма внутренниходностороннихуглов равна 180°

АксиомаПроисходит от греческого «аксиос»,что означает «ценный, достойный».Положение, принимаемое безлогического доказательства в силунепосредственной убедительности,истинное исходное положение теории.Советский энциклопедический словарь

Сколько прямых можно провести через любые две точки, лежащие на плоскости? Через любые две точкипроходит прямая, и притомтолько одна

Сколько отрезков данной длины можно отложить от начала луча? На любом луче от его начала можно отложить отрезок, равный данному, ипритом только один

Сколько углов равных данному можноотложить от данного луча в заданную полуплоскость? От любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один
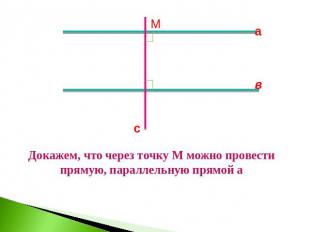
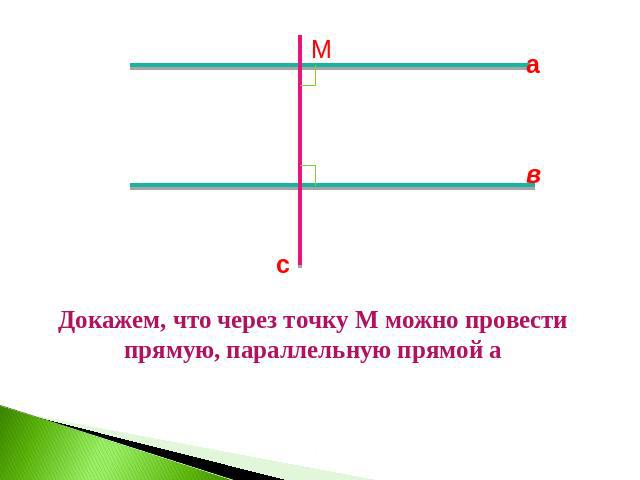
Докажем, что через точку М можно провести прямую, параллельную прямой а
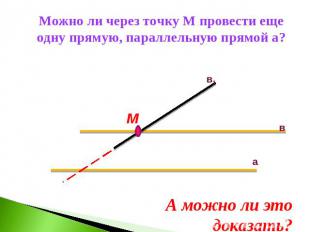
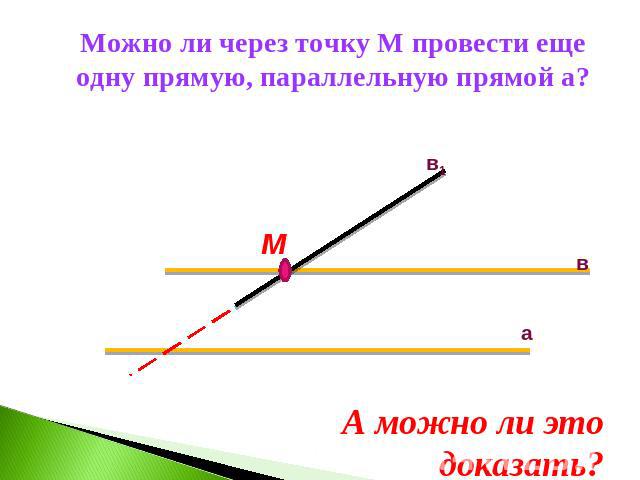
Можно ли через точку М провести еще одну прямую, параллельную прямой а?А можно ли это доказать?

Пятый постулатЕвклида1792-1856Николай Иванович Лобачевский

«Через точку, не лежащую на данной прямой,проходит только одна прямая, параллельнаяданной».«Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной».Какое из данных утверждений является аксиомой?Чем отличаются вышеуказанные утверждения ?
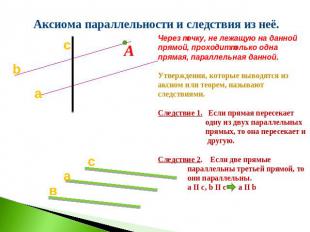
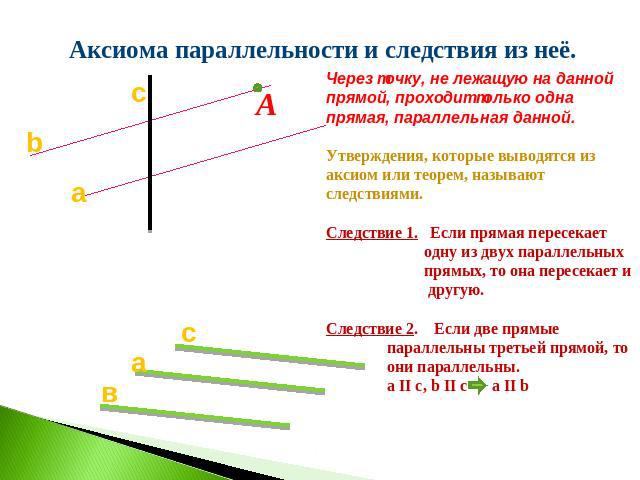
Аксиома параллельности и следствия из неё. Через точку, не лежащую на даннойпрямой, проходит только однапрямая, параллельная данной.Утверждения, которые выводятся из аксиом или теорем, называют следствиями.Следствие 1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны. a II с, b II с a II b

Отметить знаком «+» правильные утверждения и знаком «-» - ошибочные. Вариант 11. Аксиомой называетсяматематическое утверждение о свойствах геометрических фигур, требующее доказательства.2. Через любые две точки проходит прямая.3. На любом луче от начала можно отложить отрезки, равные данному, причем сколько угодно много.4.Через точку не лежащую наданной прямой, проходит только одна прямая, параллельная данной.5. Если две прямые параллельны третьей, то они параллельны между собой. Вариант 21. Аксиомой называетсяматематическое утверждение освойствах геометрических фигур,принимаемое без доказательства.2. Через любые две точки проходитпрямая, и притом только одна.3. Через точку, не лежащую наданной прямой, проходят толькодве прямые, параллельныеданной.4. Если прямая пересекает одну издвух параллельных прямых, то онаперпендикулярна другой прямой.5. Если прямая пересекает одну издвух параллельных прямых, то онапересекает и другую.