Презентация на тему: Параллельные прямые. Признаки параллельности прямых

Параллельные прямые Признаки параллельности прямых

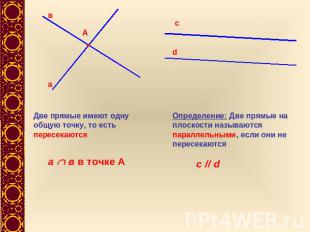
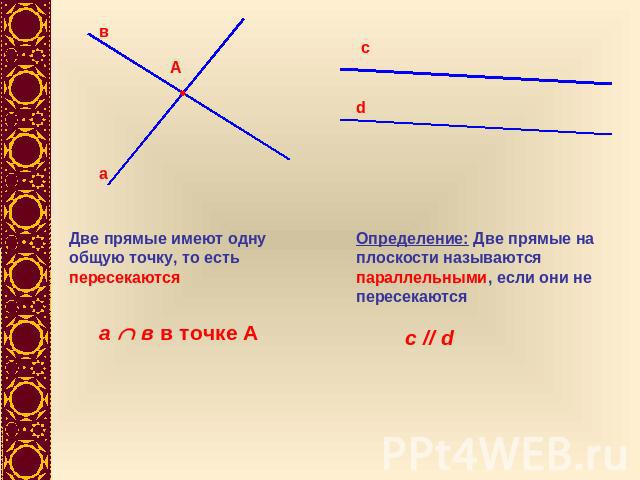
Две прямые имеют одну общую точку, то есть пересекаются Определение: Две прямые на плоскости называются параллельными, если они не пересекаются

Накрест лежащие углы – 3 и 5; 4 и 6.Односторонние углы – 4 и 5; 3 и 6.Соответственные углы – 1 и 5; 2 и 6; 4 и 8; 3 и 7.

Признаки параллельности двух прямых

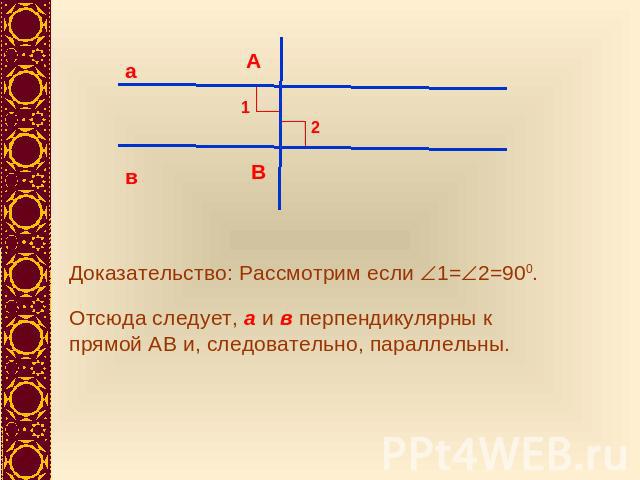
Теорема: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.Дано: а, в – прямые, АВ – секущая, 1 и 2 – накрест лежащие, 1=2.

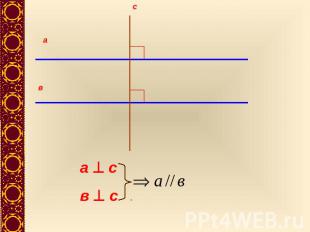
Доказательство: Рассмотрим если 1=2=900.Отсюда следует, а и в перпендикулярны к прямой АВ и, следовательно, параллельны.

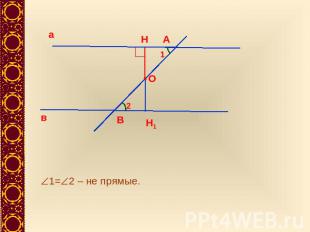
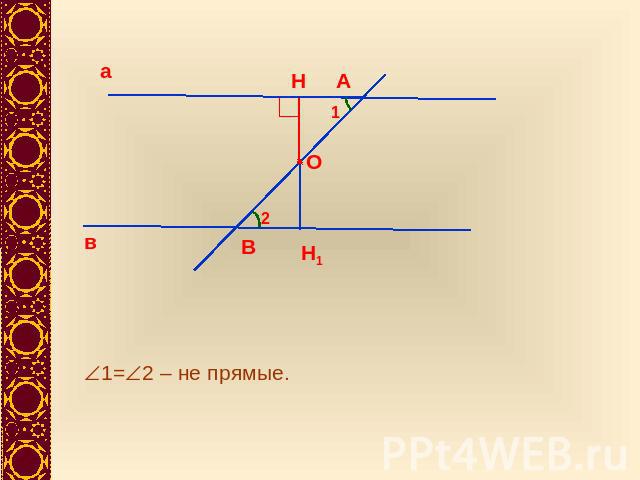
1=2 – не прямые.

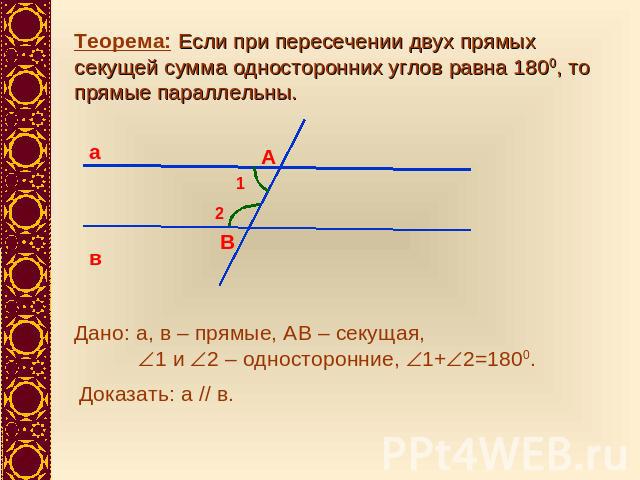
Теорема: Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.Дано: а, в – прямые, АВ – секущая, 1 и 2 – односторонние, 1+2=1800.

Доказательство: 1+3=1800 – сумма смежных углов.1+2=1800 – по условию теоремы.Так как 2=3 – по выше доказанной теореме (Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.) следует, что а//в.

Теорема: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.Дано: а, в – прямые, АВ – секущая, 1 и 2 – соответственные, 1=2 .

Доказательство: 1=3 – вертикальные углы.1=2 – по условию теоремы.Так как 2=3 – по выше доказанной теореме (Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.) следует, что а//в.