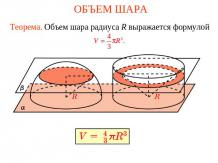
Презентация на тему: Подобные треугольники
Подобные треугольники Учитель школы №20Смотрина Валентина Петровна

Содержание Начать просмотрПодобные фигурыПодобные треугольникиОтношение периметров подобных треугольниковОтношение площадей подобных треугольников
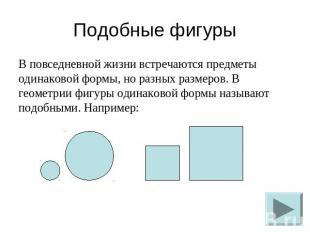
Подобные фигуры В повседневной жизни встречаются предметы одинаковой формы, но разных размеров. В геометрии фигуры одинаковой формы называют подобными. Например:

Подобные треугольники Мы видим что соответственные углы не меняются т. е.A=A1, B=B1, C=C1.Стороны изменились по длине.AB и A1B1, BC и B1C1, CA и C1A1 называют сходственными.Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.Другими словами, два треугольника подобны, если можно обозначить буквами ABC и A1B1C1 так, чтоA=A1; B=B1; C=C1,AB:A1B1=BC:B1C1=CA:C1A1=k.Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.
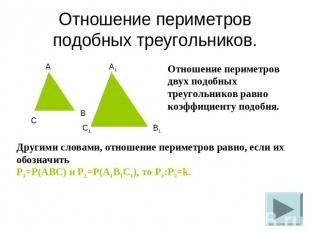
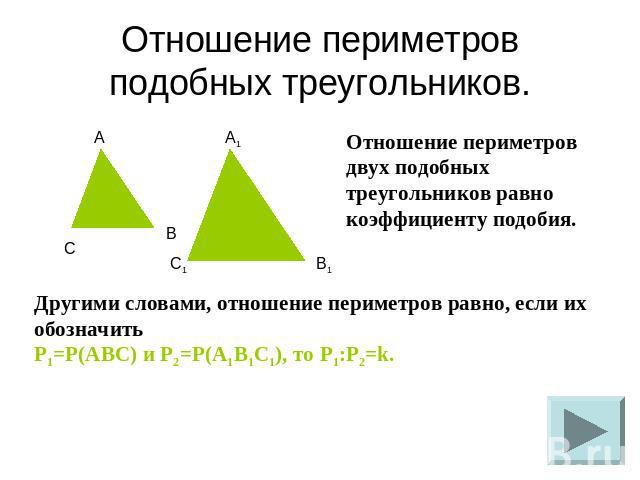
Отношение периметров подобных треугольников. Отношение периметров двух подобных треугольников равно коэффициенту подобия.Другими словами, отношение периметров равно, если их обозначитьP1=P(ABC) и P2=P(A1B1C1), то P1:P2=k.
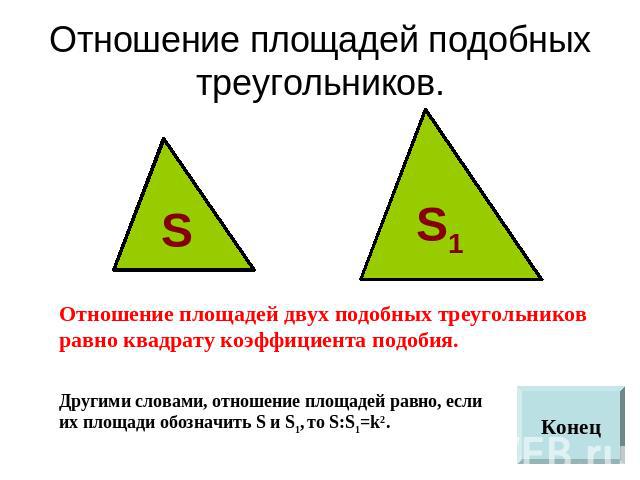
Отношение площадей подобных треугольников. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.Другими словами, отношение площадей равно, если их площади обозначить S и S1, то S:S1=k2.