Презентация на тему: Подобные треугольники

Геометрия Треугольник 900igr.net

Содержание: 1) Давайте вспомним. 2)Подобные фигуры 3)Определение подобных треугольников 4)Признаки подобия треугольника 5) Это интересно. 6) Еще немного о треугольниках.

Давайте вспомним Треугольник- это геометрическая фигура состоящая из трех точек не лежащие на прямой и трех отрезков, попарно соединяющих эти точки. Эти точки называются вершинами треугольника, а отрезки сторонами треугольника.

Подобные фигуры Чем похожи фигуры? ФОРМОЙ!

Определение подобных треугольников Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Признаки подобия треугольников 1 Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. 2 Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны. 3 Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

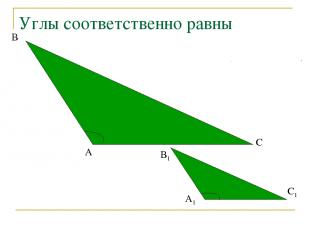
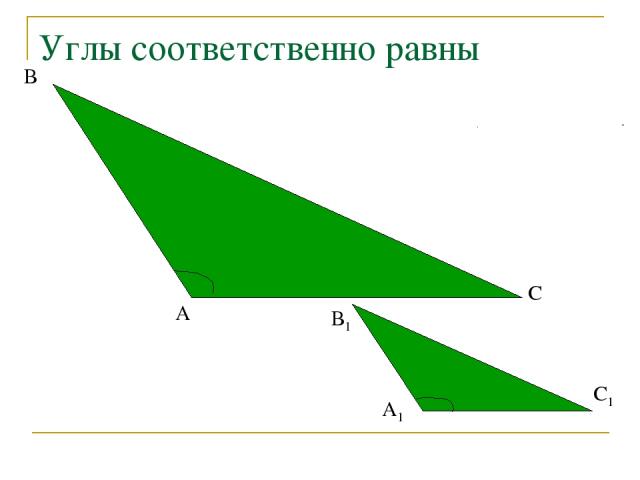
Углы соответственно равны А В С В1 А1 С1

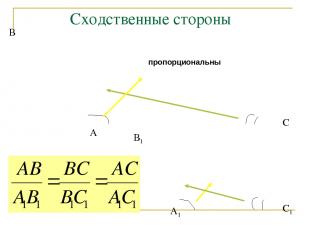
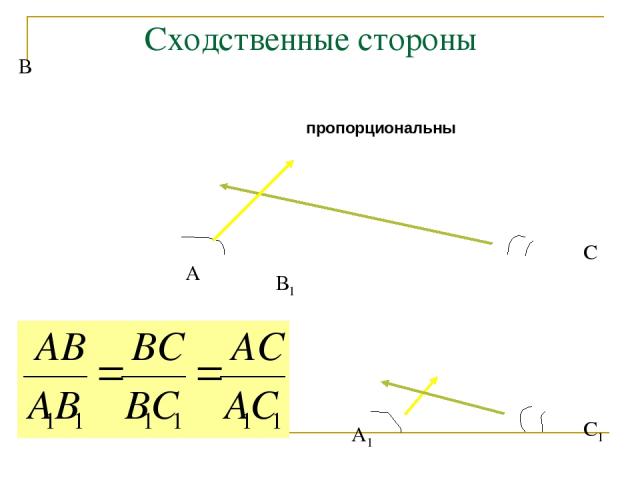
Сходственные стороны В А С В1 А1 С1 пропорциональны

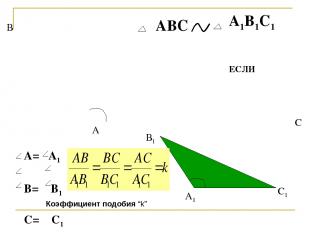
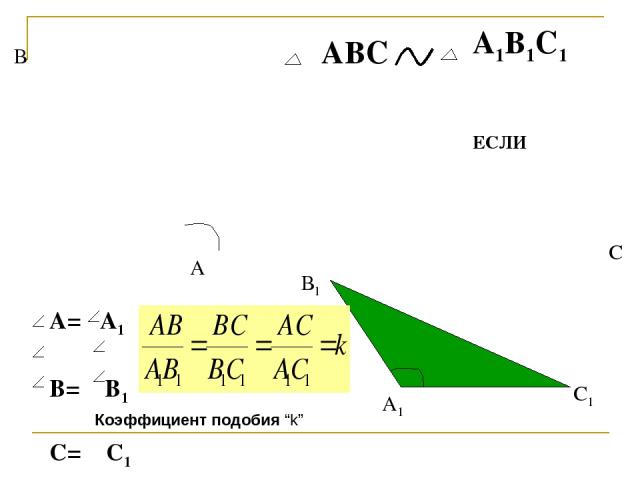
АВС А1В1С1 ЕСЛИ А= А1 В= В1 С= С1 А В С А1 В1 С1 Коэффициент подобия “k”

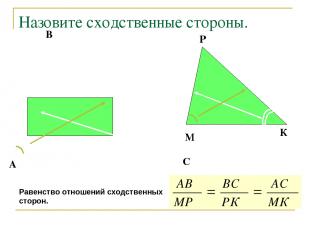
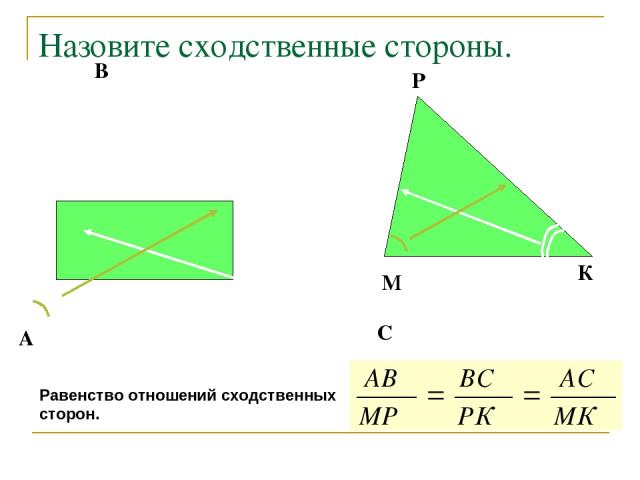
Назовите сходственные стороны. А С В М К Р Равенство отношений сходственных сторон.

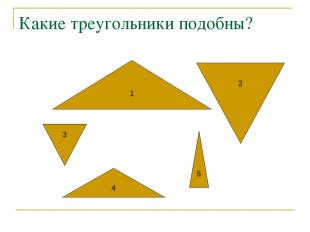
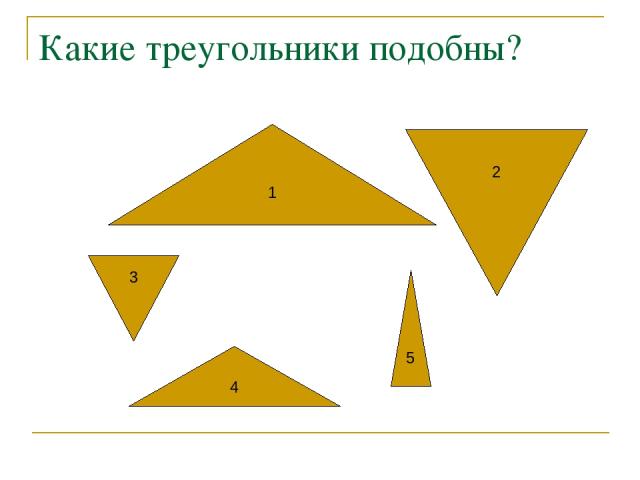
Какие треугольники подобны? 1 4 2 3 5

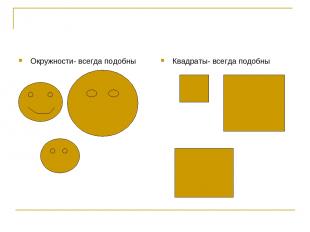
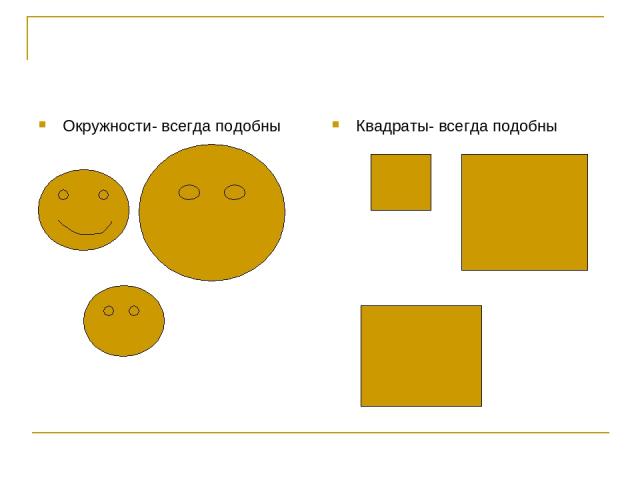
Окружности- всегда подобны Квадраты- всегда подобны

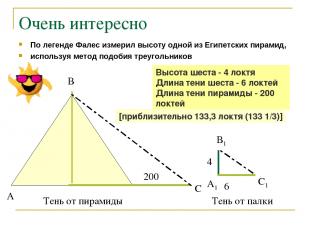
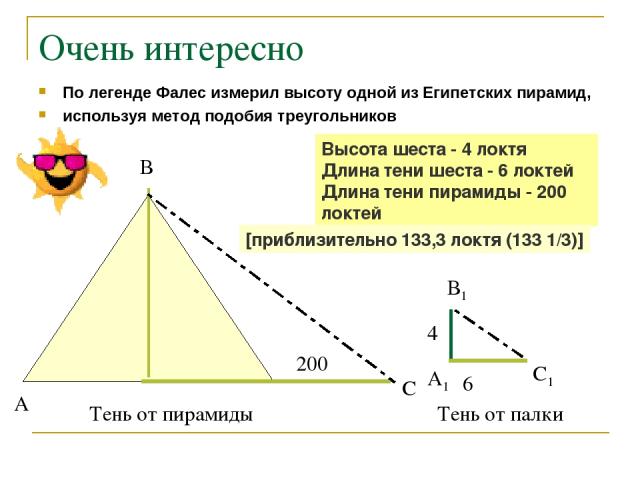
Очень интересно По легенде Фалес измерил высоту одной из Египетских пирамид, используя метод подобия треугольников 200 6 4 А В С А1 В1 С1 Тень от пирамиды Тень от палки Высота шеста - 4 локтя Длина тени шеста - 6 локтей Длина тени пирамиды - 200 локтей [приблизительно 133,3 локтя (133 1/3)]

Еще немного о треугольниках.

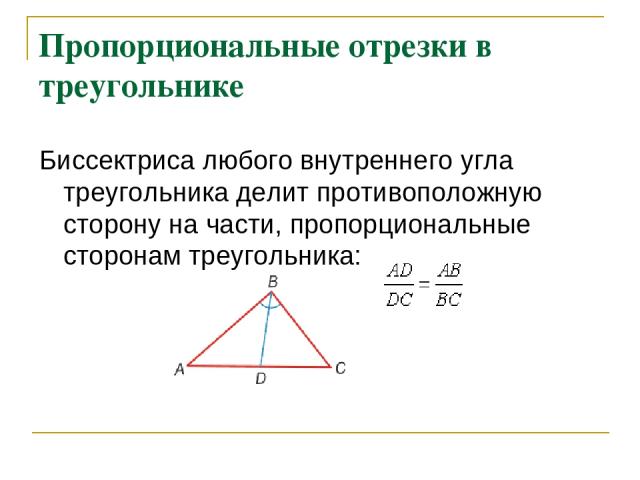
Пропорциональные отрезки в треугольнике Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника:

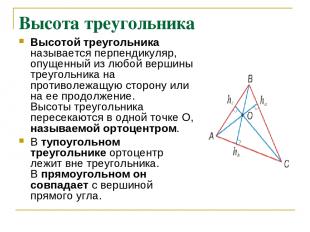
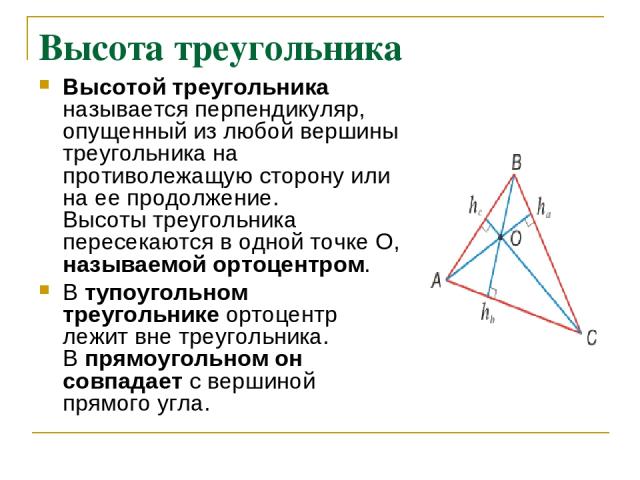
Высота треугольника Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение. Высоты треугольника пересекаются в одной точке О, называемой ортоцентром. В тупоугольном треугольнике ортоцентр лежит вне треугольника. В прямоугольном он совпадает с вершиной прямого угла.

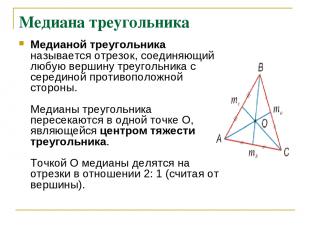
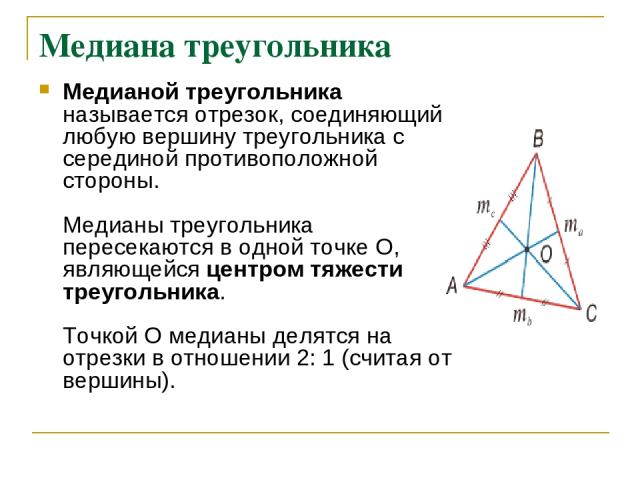
Медиана треугольника Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Медианы треугольника пересекаются в одной точке О, являющейся центром тяжести треугольника. Точкой О медианы делятся на отрезки в отношении 2: 1 (считая от вершины).

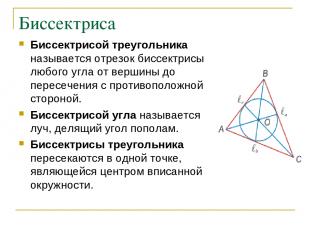
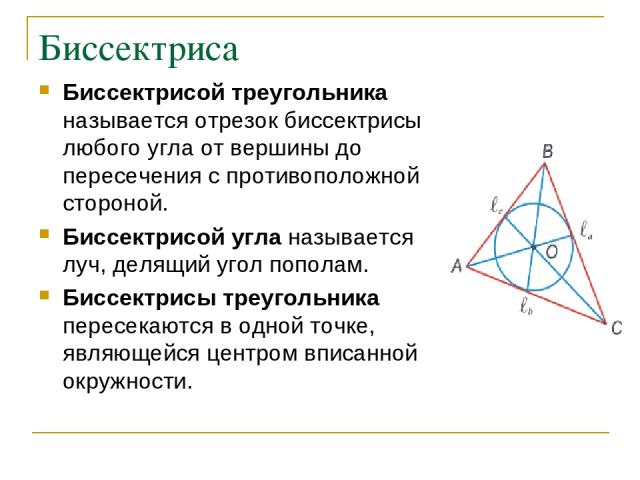
Биссектриса Биссектрисой треугольника называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной. Биссектрисой угла называется луч, делящий угол пополам. Биссектрисы треугольника пересекаются в одной точке, являющейся центром вписанной окружности.

Проект подготовила Ученица 8 Б класса Мертвищева Екатерина СПАСИБО ЗА ВНИМАНИЕ!!!