Презентация на тему: Подобные треугольники (2)

Рассмотрим пропорцию: Рассмотрим пропорцию: Отрезки называются пропорциональными, если равны отношения их длин.

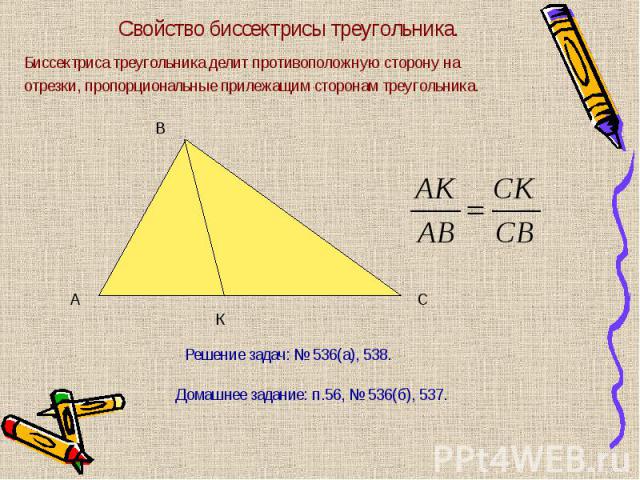
Биссектриса треугольника делит противоположную сторону на Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

Два треугольника называются подобными, если их углы соответственно равны, и стороны од- ного треугольника пропорциональны соответ- ствующим сторонам другого треугольника. где k – коэффициент подобия. Говорят, что ∆АВС ~ ∆МРК

ТЕОРЕМА. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. где k – коэффициент подобия. Отношение периметров двух подобных треугольников равно коэффициенту подобия.

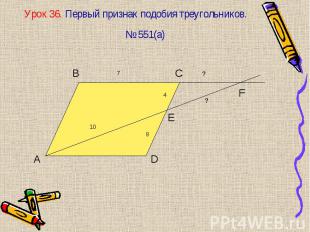
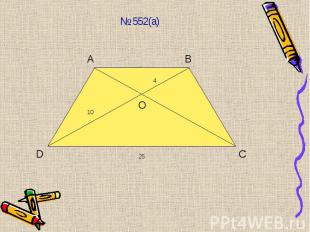
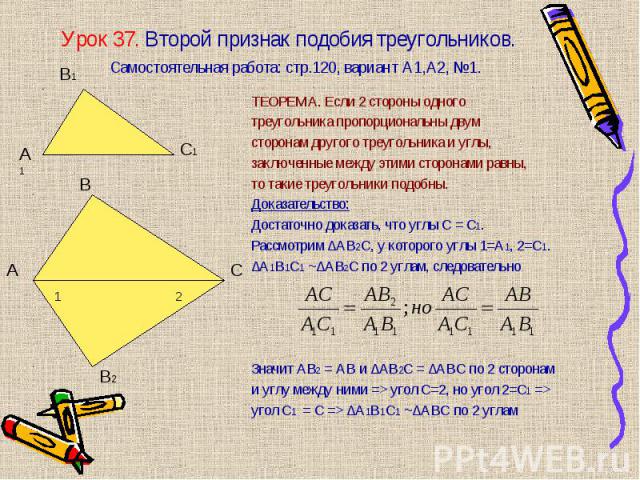
ТЕОРЕМА. Если 2 стороны одного ТЕОРЕМА. Если 2 стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами равны, то такие треугольники подобны. Доказательство: Достаточно доказать, что углы С = С1. Рассмотрим ∆АВ2С, у которого углы 1=А1, 2=С1. ∆А1В1С1 ~∆АВ2С по 2 углам, следовательно Значит АВ2 = АВ и ∆АВ2С = ∆АВС по 2 сторонам и углу между ними => угол С=2, но угол 2=С1 => угол С1 = С => ∆А1В1С1 ~∆АВС по 2 углам

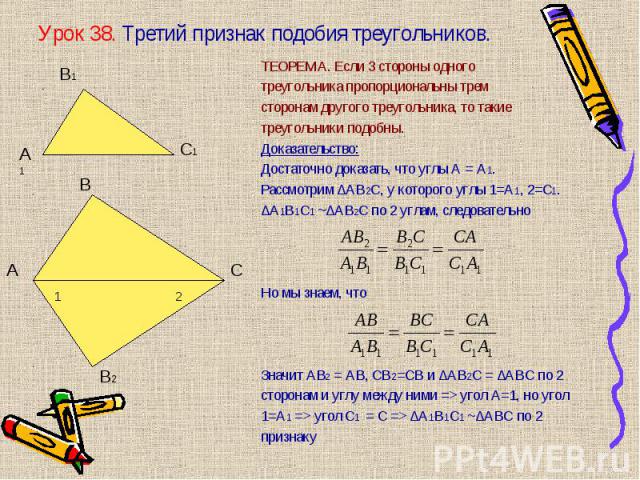
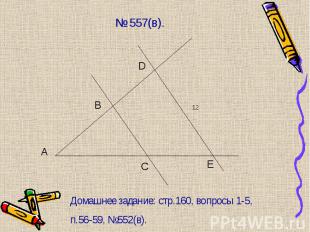
ТЕОРЕМА. Если 3 стороны одного ТЕОРЕМА. Если 3 стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Доказательство: Достаточно доказать, что углы А = А1. Рассмотрим ∆АВ2С, у которого углы 1=А1, 2=С1. ∆А1В1С1 ~∆АВ2С по 2 углам, следовательно Но мы знаем, что Значит АВ2 = АВ, СВ2=СВ и ∆АВ2С = ∆АВС по 2 сторонам и углу между ними => угол А=1, но угол 1=А1 => угол С1 = С => ∆А1В1С1 ~∆АВС по 2 признаку

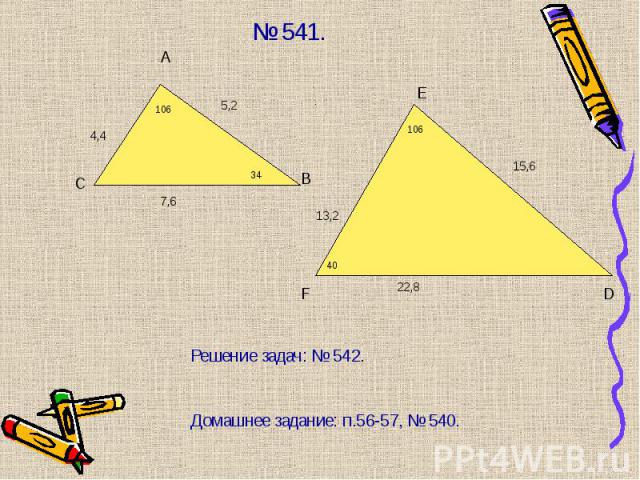
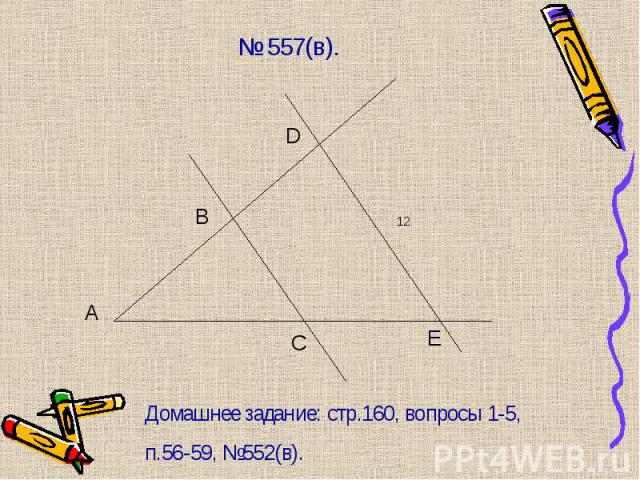
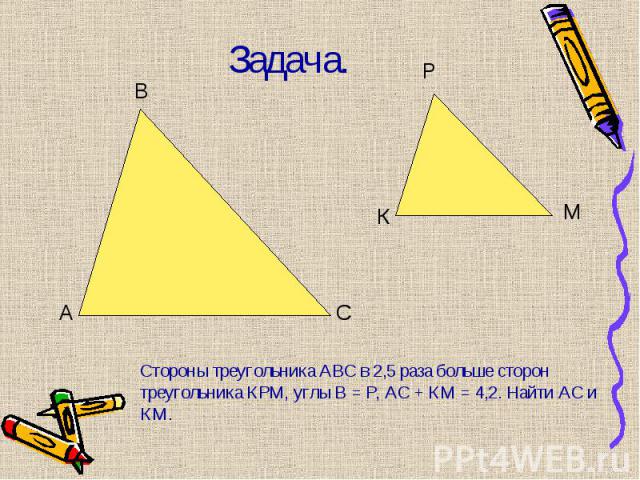
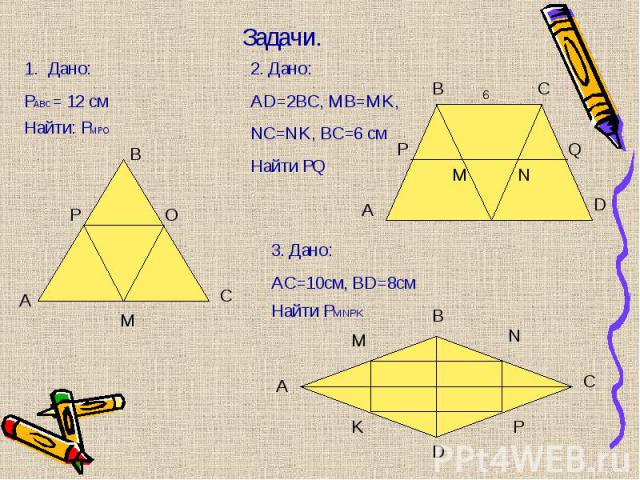
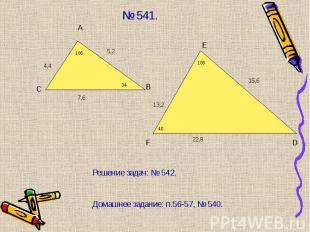
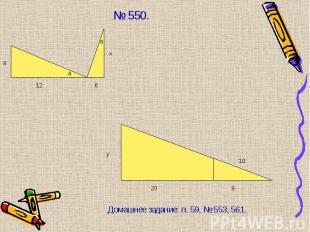
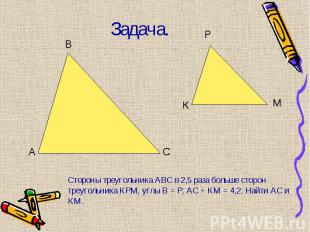
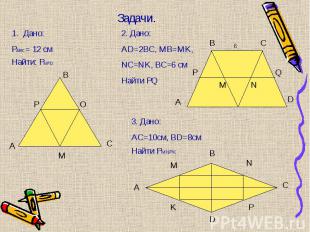
Подобны ли ∆АВС и ∆КРМ, если АВ = 1м, АС = 2м, ВС = 1,5 м, КР = 8 дм, КМ = 16 дм, РМ = 12 дм. Подобны ли ∆АВС и ∆КРМ, если АВ = 1м, АС = 2м, ВС = 1,5 м, КР = 8 дм, КМ = 16 дм, РМ = 12 дм. Стороны треугольника равны 0,8 м, 1,6 м, 2 м. Найти стороны подобного ему треугольника, периметр которого равен 5,5 м. Домашнее задание: п. 59-61, № 560.

Третий признак подобия треугольников. Третий признак подобия треугольников. Второй признак подобия треугольников. У двух треугольников по одному равному углу. Какого условия недостает, чтобы треугольники были подобны по 1 признаку? Стороны одного треугольника равны 3 см, 6 см и 7 см, а 2 стороны подобного ему треугольника равны 15 см и 35 см. Найти третью сторону. Соответствующие катеты двух подобных треугольников 6 дм и 18 дм. Найти гипотенузу меньшего треугольника, если гипотенуза большего 27 дм.

По 3 пропорциональ-ным сторонам. По 3 пропорциональ-ным сторонам. По 2 пропорциональ-ным сторонам и углу между ними. Пара равных углов. 30 см. 9 дм.

Два прямоугольных треугольника подобны, если: Два прямоугольных треугольника подобны, если: У них есть по равному острому углу. Катеты одного треугольника пропорциональны катетам другого треугольника. Гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.

ТЕОРЕМА. ТЕОРЕМА. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Доказательство: ∆АВС ~ ∆КВР, так как угол В-общий, а стороны АВ и КВ, СВ и РВ пропорциональны => угол А=ВКР, но это соответственные углы => КР ll АС.

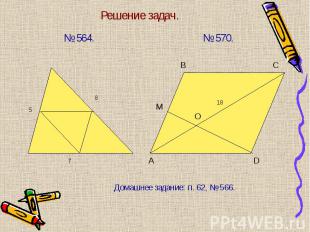
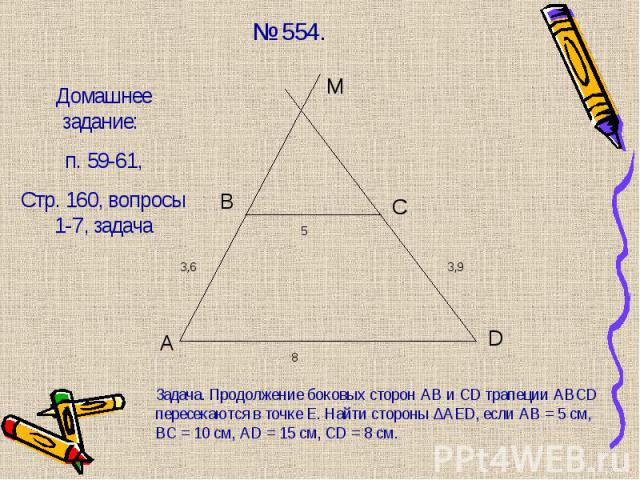
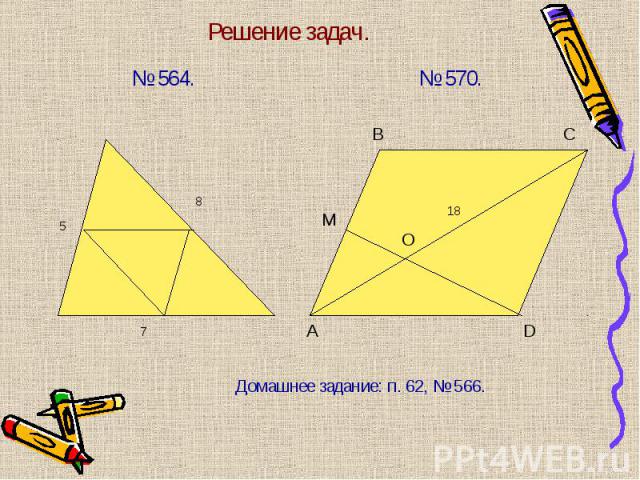
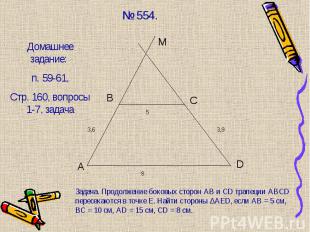
№ 564. № 564.

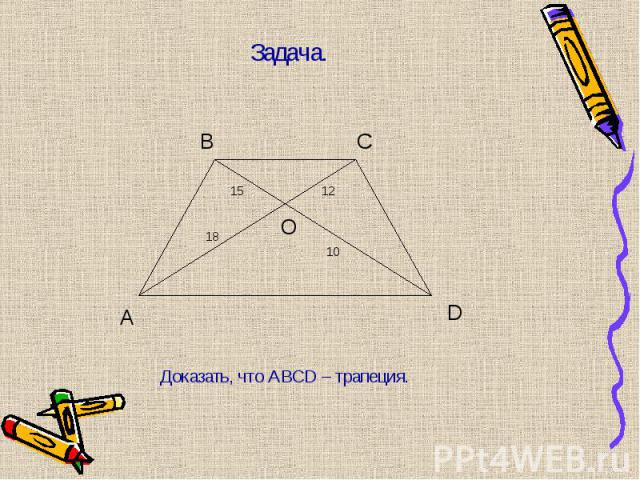
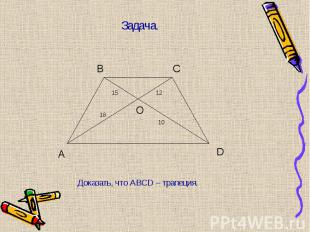
Две стороны треугольника соединили отрезком, непараллельным третьей стороне. Является ли этот отрезок средней линией треугольника? Две стороны треугольника соединили отрезком, непараллельным третьей стороне. Является ли этот отрезок средней линией треугольника? Сторона АВ ∆АВС равна 6 см. Чему равна средняя линия треугольника, параллельная этой стороне? Точки М, Р и О – середины сторон ∆АВС. Найти стороны ∆АВС, если стороны ∆МРО равны 3 см, 4 см и 5 см. Концы отрезка АВ лежат на двух сторонах треугольника, а длина этого отрезка равна половине третьей стороны. Обязательно ли этот отрезок является средней линией треугольника?

Нет Нет Средняя линия 24 см Нет

Признак подобия прямоугольных Признак подобия прямоугольных треугольников. Два прямоугольных треугольника подобны, если у них есть по равному острому углу. Отрезок XY называется средним пропорциональным (средним геометрическим) для отрезков АВ и CD, если Свойство 1. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу. Свойство 2. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

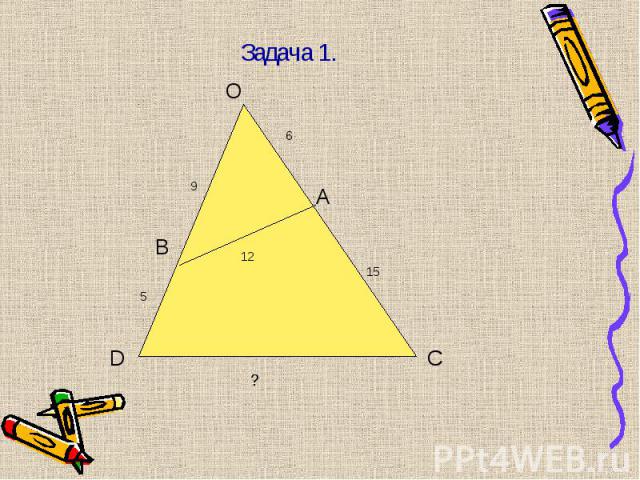
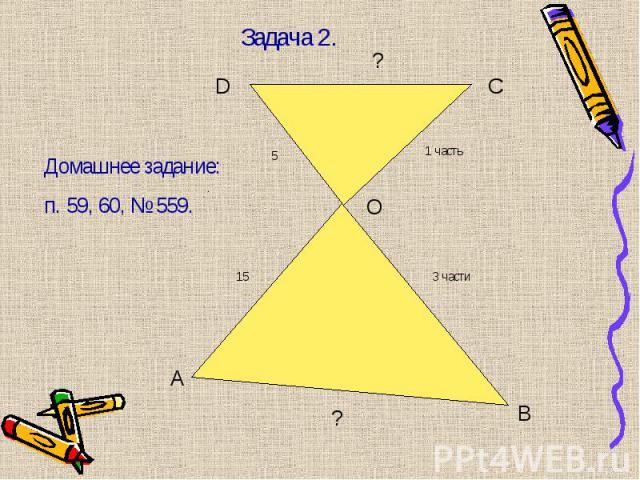
Решение задач: № 572, 575, 577. Решение задач: № 572, 575, 577. Домашнее задание: стр.160, вопросы 8-11, принести циркуль, № 576, 578-в общую тетрадь. Проверочная работа. стр. 124, вариант А1, А2, задачи 1, 2.

Найти площадь равнобедренного прямоугольного треугольника с основанием 10 см и углом при основании 45°. Найти площадь равнобедренного прямоугольного треугольника с основанием 10 см и углом при основании 45°. Найти катеты прямоугольного треугольника, гипотенуза которого 2 см, один из острых углов 30°. В треугольнике АВС угол А=45°, угол С=60°, ВС=2 см. Найти АС. № 600. Домашнее задание: п. 66, 67, № 602.

Средняя линия равнобед-ренного треугольника, параллельная боковой стороне, равна 13 см, а медиана, проведенная к основанию - 24 см. Найти среднюю линию, парал-лельную основанию треугольника. Средняя линия равнобед-ренного треугольника, параллельная боковой стороне, равна 13 см, а медиана, проведенная к основанию - 24 см. Найти среднюю линию, парал-лельную основанию треугольника. Найти sin α и tg α, если cosα=8/17. Найти синус, косинус тангенс большего острого угла прямоугольного треугольника с катетами 7 см и 24 см.