Презентация на тему: Подобные треугольники

Подобные треугольники Признаки подобия треугольников

Определение подобных треугольников Два треугольника называться подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Первый признак подобия треугольников Теорема Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

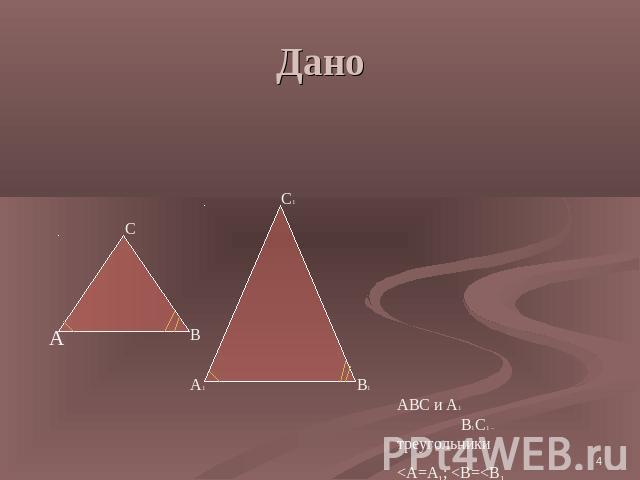
Дано

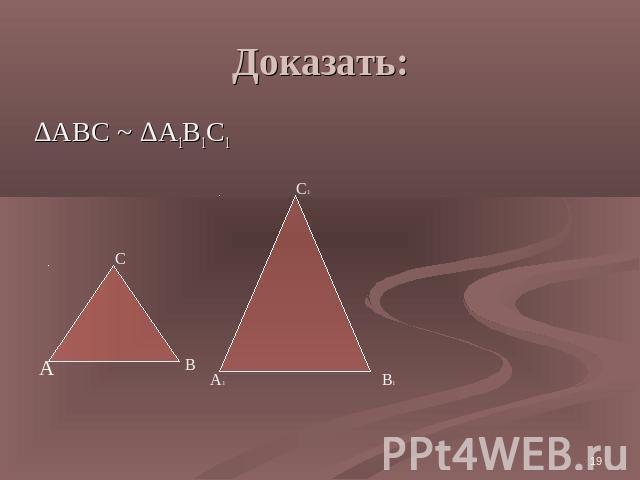
Доказать:

Доказательство: По теореме о сумме углов треугольника: С=180°-А-В,С1=180°-А1-С1,следовательно угол С равен углу С1 .Значит, углы треугольника АВС соответственно равны углам треугольника А1В1С1.

Доказательство: Докажем ,что стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1.Т.к <А=<А1 и <С=<С1,то SABC ∕ SA1B1C1=AB·AC ∕ A1B1·A1C1 и SABC∕ SA1B1C=CA·CB ∕ C1A1·C1B1

Доказательство: Из равенств пункта 2 следует, что АВ∕ А1В1=ВС ∕ В1С1.Аналоггично,используя равенства <A=<A1, <B=<B1,получаем BC\B1C1=CA\C1A1.

Доказательство: Из равенств пункта 2 следует, что АВ∕ А1В1=ВС ∕ В1С1.Аналоггично,используя равенства <A=<A1, <B=<B1, получаем ВС/B1C1=CA/C1A1 .

Что и требовалось доказать Итак, стороны треугольника АВС пропорциональны сходственным сторонам треугольника А1В1С1. Теорем доказана.

Второй признак подобия треугольников. Теорема:Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Дано

Доказательство: Для того, чтобы доказать данную теорему, нужно учитывать первый признак подобия треугольников, доказанный выше. Поэтому достаточно доказать, что <B=<B1.

Доказательство: Рассмотрим треугольник АВС2,у которого <1=<A1, <2=<B1.∆ABC2~∆A1B1C1(по первому признаку подобия)

Доказательство: Значит, AB/A1B1=AC2/A1C С другой стороны AB/A1B1=AC/A1C1(по условию).Получаем АС=АС2∆АВС и ∆АВС2 равны по двум сторонам и углу межу ними(АВ- общая сторона, АС=АС2 и <A=<1,т.к <A=<A1 и <1=<A1)

Что и требовалось доказать: Следует, что <B=<2, а так как <2=<B1,то <B=<B1. Теорема доказана.

Третий признак подобия треугольников Доказательство теоремы

Теорема: Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

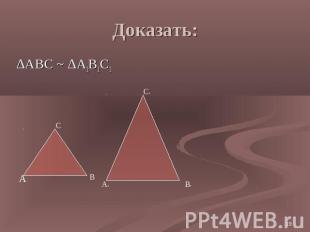
Доказать:

Доказательство: Учитывая второй признак подобия треугольников, достаточно доказать, что <A=<A1.Рассмотрим треугольник АВС2,у которого <1=<A1, <2=<B1.

Доказательство:

Доказательство: Треугольники АВС2 и А1В1С1 подобны по первому признаку подобия треугольников, поэтому АВ/A1B1=BC2/B1C1 =C2A/C1A1.

Что и требовалось доказать: Получаем: ВС=ВС2, СА=С2А. Треугольники АВС и АВС2 равны по трем сторонам. отсюда следует, что <А=<1,а так как <1=<A1, <A=<A1.

Выполнила ученица 10Б Смоленышева Анастасия