Презентация на тему: Перпендикулярность плоскостей

ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ Две плоскости называются перпендикулярными, если угол между ними прямой.Теорема. (Признак перпендикулярности двух плоскостей.) Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.Пусть плоскость α проходит через прямую a, перпендикулярную плоскости β, c – линия пересечения плоскостей α и β. Докажем, что плоскости α и β перпендикулярны. В плоскости β через точку пересечения прямой a с плоскостью β проведем прямую b, перпендикулярную прямой c. Через прямые a и b проведем плоскость γ. Прямая c будет перпендикулярна плоскости γ, так как она перпендикулярна двум пересекающимся прямым a и b в этой плоскости. Поскольку прямая a перпендикулярна плоскости β, то угол, образованный a и b, прямой. Он является линейным углом соответствующего двугранного угла. Следовательно, плоскости α и β перпендикулярны.

Упражнение 1 Верно ли, что две плоскости, перпендикулярные третьей, параллельны?

Упражнение 2 Сколько плоскостей, перпендикулярных данной плоскости, можно провести через данную прямую?Ответ: Бесконечно много, если прямая перпендикулярна плоскости, и одну в противном случае.

Упражнение 3 Плоскость α перпендикулярна плоскости β. Будет ли всякая прямая плоскости α перпендикулярна плоскости β?

Упражнение 4 Плоскость и прямая параллельны. Верно ли утверждение о том, что плоскость, перпендикулярная данной плоскости, перпендикулярна и данной прямой?

Упражнение 5 Плоскость и прямая параллельны. Будет ли верно утверждение о том, что плоскость, перпендикулярная прямой, перпендикулярна и данной плоскости?

Упражнение 6 Равнобедренный прямоугольный треугольник ABC( C = 90°) перегнули по высоте CD таким образом, что плоскости ACD и BCD образовали прямой угол. Найдите углы ADB и ACB.

Упражнение 7 Существует ли треугольная пирамида, у которой три грани попарно перпендикулярны?

Упражнение 8 Существует ли четырехугольная пирамида, у которой две противоположные боковые грани перпендикулярны основанию?

Упражнение 9 Существует ли пирамида, у которой три боковые грани перпендикулярны основанию?

Упражнение 10 Могут ли боковыми гранями наклонной призмы быть: а) 2 прямоугольника; б) 3 прямоугольника; в) 4 прямоугольника?

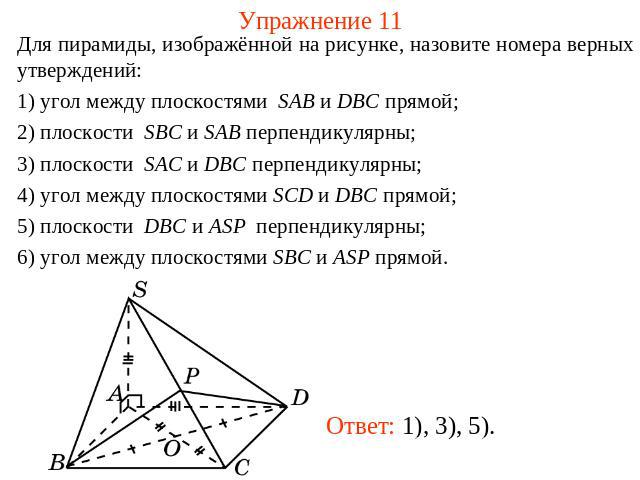
Упражнение 11 Для пирамиды, изображённой на рисунке, назовите номера верных утверждений:1) угол между плоскостями SAB и DBC прямой; 2) плоскости SBC и SAB перпендикулярны;3) плоскости SAC и DBC перпендикулярны;4) угол между плоскостями SCD и DBC прямой; 5) плоскости DBC и ASP перпендикулярны;6) угол между плоскостями SBC и ASP прямой.