Презентация на тему: Перпендикулярность прямых. Перпендикулярность прямой и плоскости. Перпендикулярность плоскостей. Проверь себя

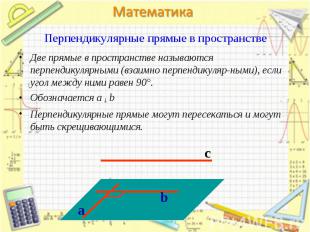
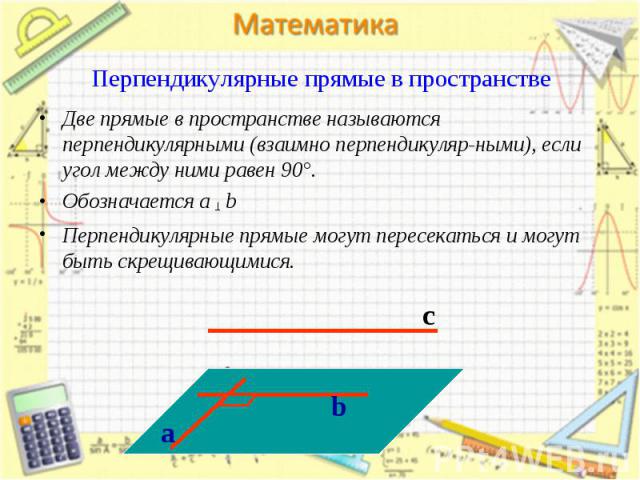
Две прямые в пространстве называются перпендикулярными (взаимно перпендикуляр-ными), если угол между ними равен 90°. Две прямые в пространстве называются перпендикулярными (взаимно перпендикуляр-ными), если угол между ними равен 90°. Обозначается a ┴ b Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.

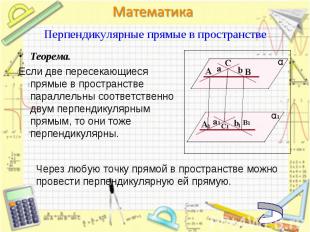
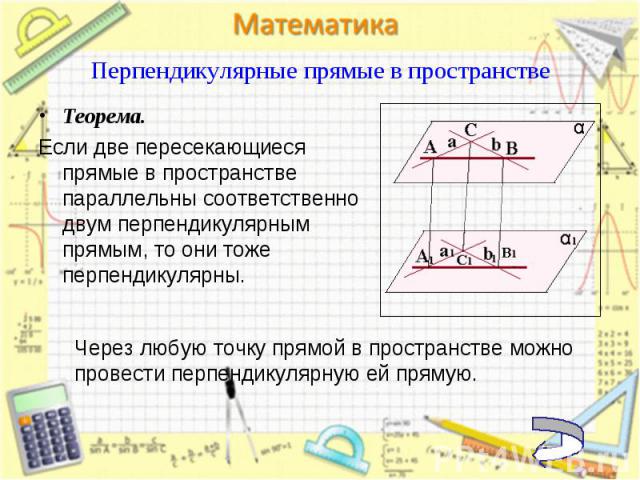
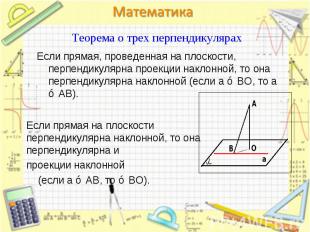
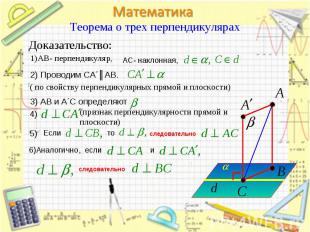
Теорема. Теорема. Если две пересекающиеся прямые в пространстве параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.

Прямая называется перпендикулярной Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

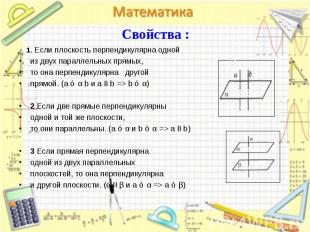
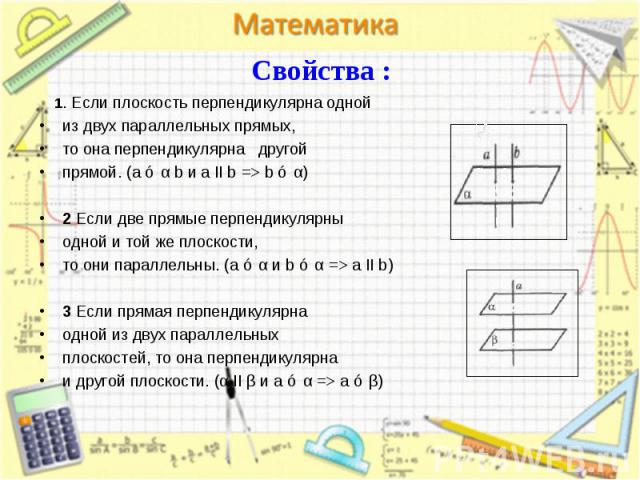
1. Если плоскость перпендикулярна одной 1. Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна другой прямой. (a ⊥ α b и a II b => b ⊥ α) 2 Если две прямые перпендикулярны одной и той же плоскости, то они параллельны. (a ⊥ α и b ⊥ α => a II b) 3 Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой плоскости. (α II β и a ⊥ α => a ⊥ β)

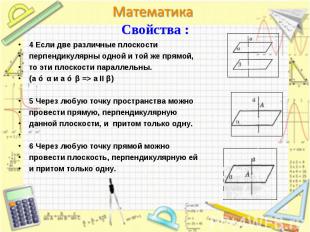
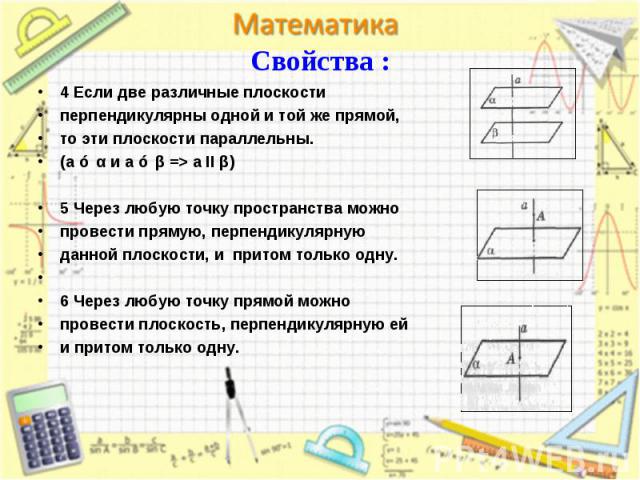
4 Если две различные плоскости 4 Если две различные плоскости перпендикулярны одной и той же прямой, то эти плоскости параллельны. (a ⊥ α и a ⊥ β => a II β) 5 Через любую точку пространства можно провести прямую, перпендикулярную данной плоскости, и притом только одну. 6 Через любую точку прямой можно провести плоскость, перпендикулярную ей и притом только одну.

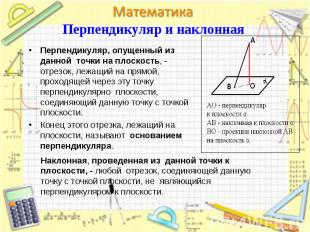
Перпендикуляр, опущенный из данной точки на плоскость, - отрезок, лежащий на прямой, проходящей через эту точку перпендикулярно плоскости, соединяющий данную точку с точкой плоскости. Перпендикуляр, опущенный из данной точки на плоскость, - отрезок, лежащий на прямой, проходящей через эту точку перпендикулярно плоскости, соединяющий данную точку с точкой плоскости. Конец этого отрезка, лежащий на плоскости, называют основанием перпендикуляра.

Конец отрезка, лежащий на плоскости, называют основанием наклонной. Конец отрезка, лежащий на плоскости, называют основанием наклонной. Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной. Свойства:

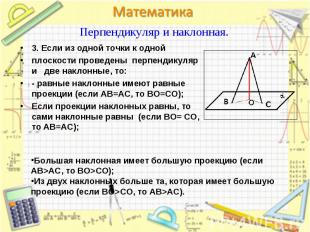
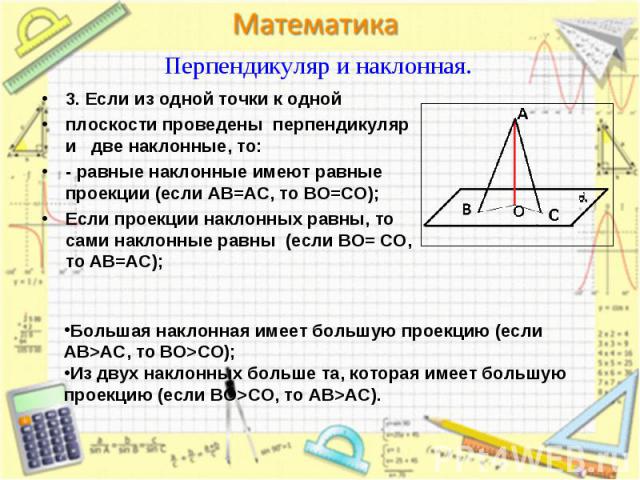
3. Если из одной точки к одной 3. Если из одной точки к одной плоскости проведены перпендикуляр и две наклонные, то: - равные наклонные имеют равные проекции (если AB=AC, то BO=CO); Если проекции наклонных равны, то сами наклонные равны (если BO= CO, то AB=AC);

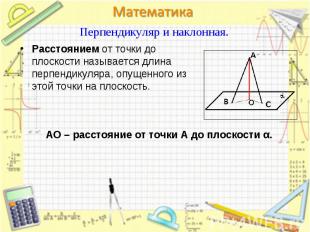
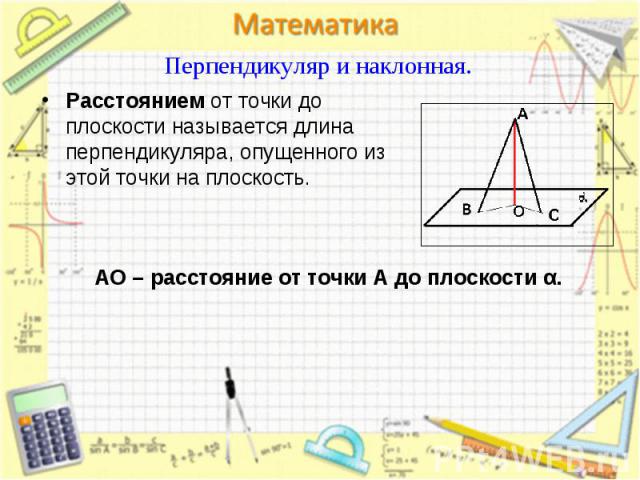
Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость. Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.

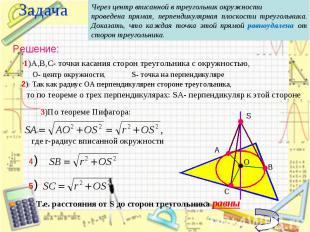
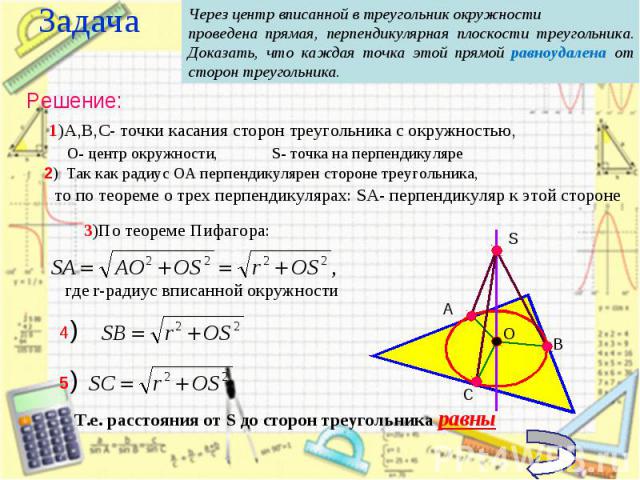
Т.е. расстояния от S до сторон треугольника равны Т.е. расстояния от S до сторон треугольника равны

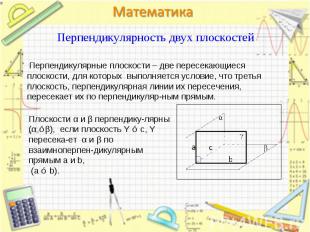
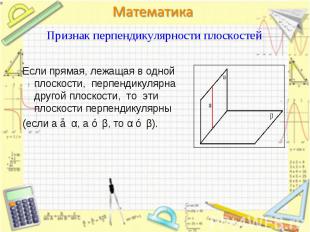
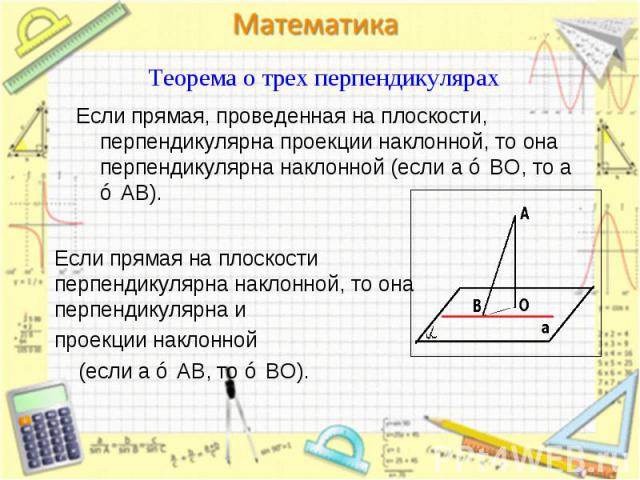
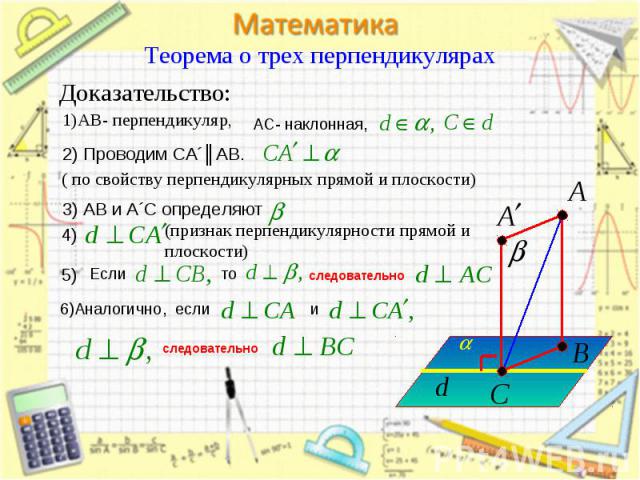
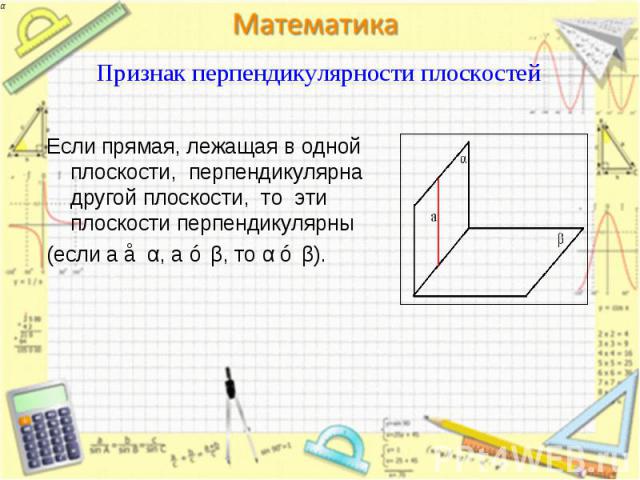
Если прямая, лежащая в одной плоскости, перпендикулярна другой плоскости, то эти плоскости перпендикулярны Если прямая, лежащая в одной плоскости, перпендикулярна другой плоскости, то эти плоскости перпендикулярны (если a ⊂ α, a ⊥ β, то α ⊥ β).

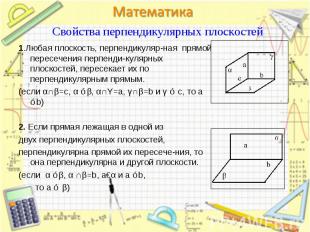
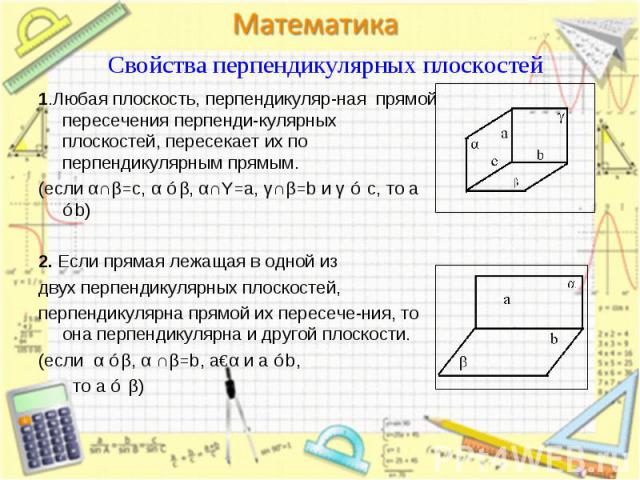
1.Любая плоскость, перпендикуляр-ная прямой пересечения перпенди-кулярных плоскостей, пересекает их по перпендикулярным прямым. 1.Любая плоскость, перпендикуляр-ная прямой пересечения перпенди-кулярных плоскостей, пересекает их по перпендикулярным прямым. (если α∩β=c, α ⊥β, α∩Υ=a, γ∩β=b и γ ⊥ c, то a ⊥b) 2. Если прямая лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна прямой их пересече-ния, то она перпендикулярна и другой плоскости. (если α ⊥β, α ∩β=b, a€α и a ⊥b, то a ⊥ β)

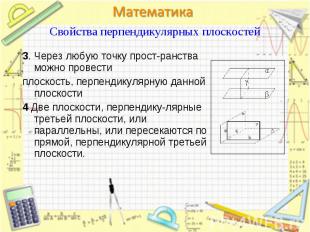
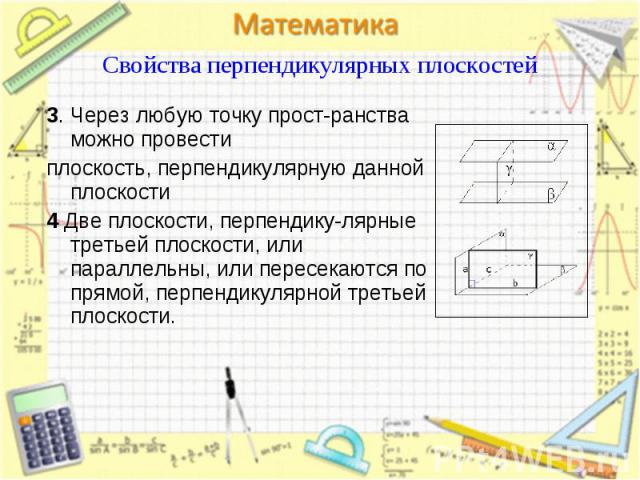
3. Через любую точку прост-ранства можно провести 3. Через любую точку прост-ранства можно провести плоскость, перпендикулярную данной плоскости 4 Две плоскости, перпендику-лярные третьей плоскости, или параллельны, или пересекаются по прямой, перпендикулярной третьей плоскости.

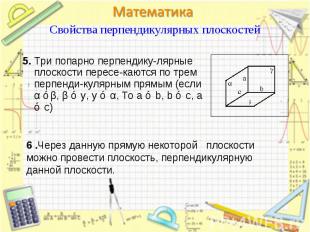
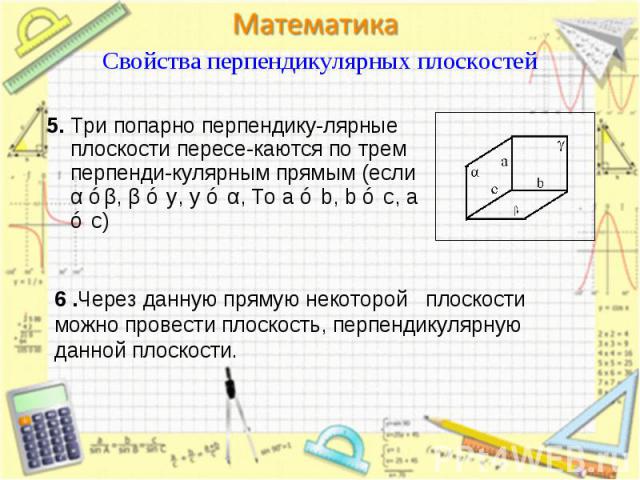
5. Три попарно перпендику-лярные плоскости пересе-каются по трем перпенди-кулярным прямым (eсли α ⊥β, β ⊥ y, y ⊥ α, То a ⊥ b, b ⊥ c, a ⊥ c) 5. Три попарно перпендику-лярные плоскости пересе-каются по трем перпенди-кулярным прямым (eсли α ⊥β, β ⊥ y, y ⊥ α, То a ⊥ b, b ⊥ c, a ⊥ c)

Двугранный угол – фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Двугранный угол – фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости. Полуплоскости называются гранями, а прямая, их ограничиваю-щая, - ребром двугранного угла.

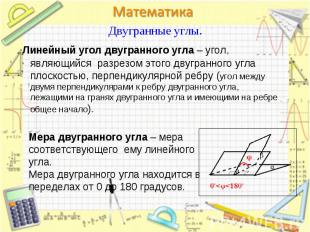
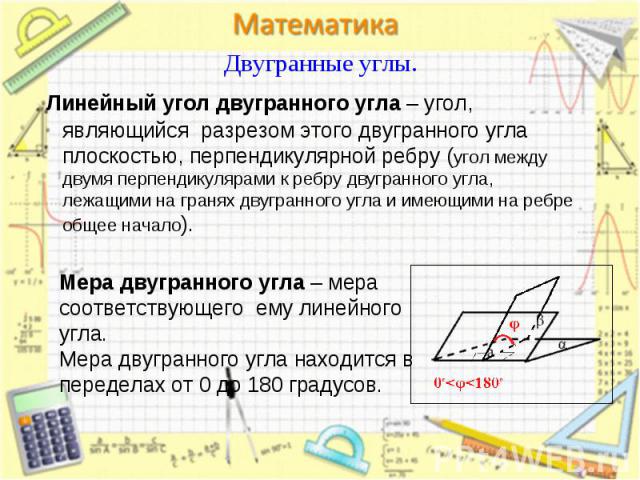
Линейный угол двугранного угла – угол, являющийся разрезом этого двугранного угла плоскостью, перпендикулярной ребру (угол между двумя перпендикулярами к ребру двугранного угла, лежащими на гранях двугранного угла и имеющими на ребре общее начало). Линейный угол двугранного угла – угол, являющийся разрезом этого двугранного угла плоскостью, перпендикулярной ребру (угол между двумя перпендикулярами к ребру двугранного угла, лежащими на гранях двугранного угла и имеющими на ребре общее начало).

Какие прямые в пространстве называются перпендикулярными? Какие прямые в пространстве называются перпендикулярными? Дайте определение перпендикулярности прямой и плоскости. Сформулируйте признак перпендикулярности прямой и плоскости. Если плоскость перпендикулярна одной из двух …. прямых , то она ,,,, другой прямой. Две прямые, перпендикулярные одной плоскости ,,,,,, Что такое перпендикуляр, опущенный из точки на плоскость? Расстояние от точки до плоскости – это … Что такое наклонная? Что такое проекция наклонной? Сформулируйте теорему о трех перпендикулярах. Какие плоскости называются перпендикулярными? Признак перпендикулярности плоскостей. Что называется расстоянием между скрещивающимися прямыми?