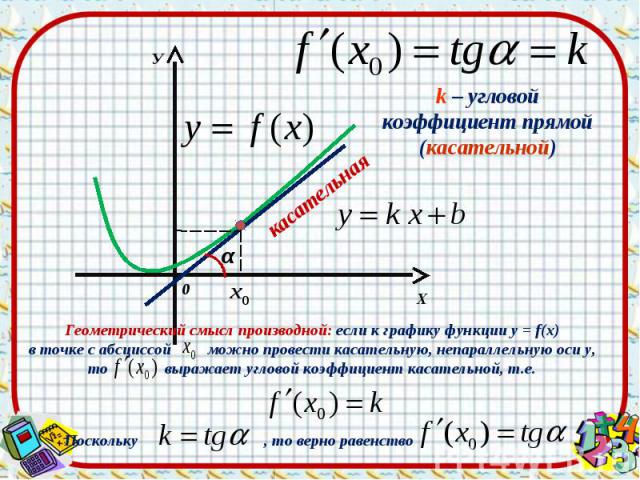
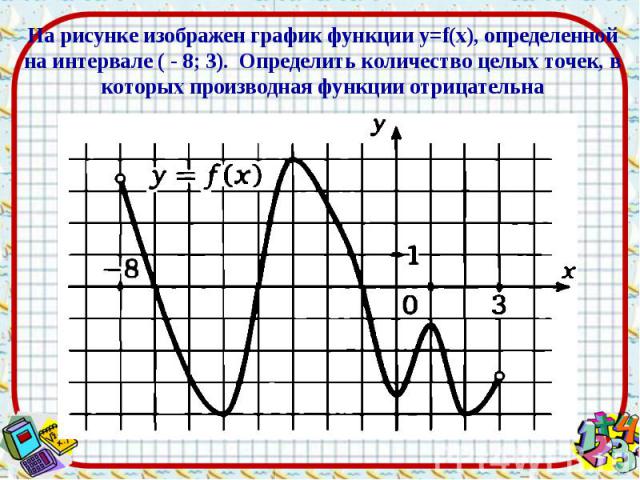
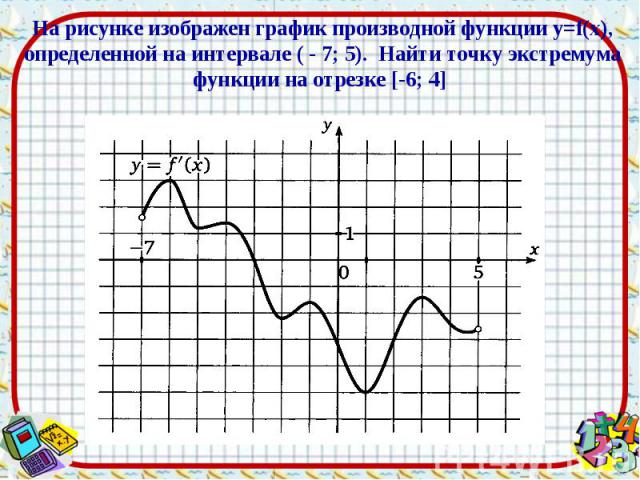
Презентация на тему: Применение производной для исследования функции на монотонность и экстремумы

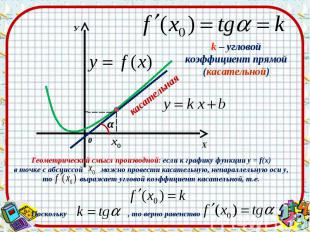
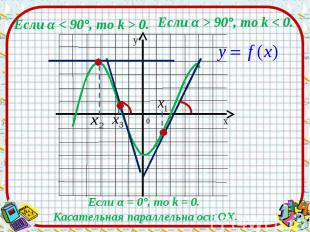
Теорема 1. Если во всех точках открытого промежутка Х выполняется неравенство f!(х)≥0 (причем равенство f!(х)=0 выполняется лишь в изолированных точках), то функция у= f(х) возрастает на промежутке Х. Теорема 1. Если во всех точках открытого промежутка Х выполняется неравенство f!(х)≥0 (причем равенство f!(х)=0 выполняется лишь в изолированных точках), то функция у= f(х) возрастает на промежутке Х. Теорема 2. Если во всех точках открытого промежутка Х выполняется неравенство f!(х)≤0 (причем равенство f!(х)=0 выполняется лишь в изолированных точках), то функция у= f(х) убывает на промежутке Х. Теорема 3. Если во всех точках открытого промежутка Х выполняется равенство f!(х)=0,то функция у= f(х) постоянна на промежутке Х.

Пример: Исследовать на монотонность функцию у=2х3+3х2 – 1. Исследовать функцию на монотонность – это значит выяснить, на каких промежутках области определения функция возрастает, а на каких – убывает. Согласно теоремам 1 и 2, это связано со знаком производной. Найдем производную данной функции:

f!(х)=6х2+6х=6х (х+1) f!(х)=6х2+6х=6х (х+1)

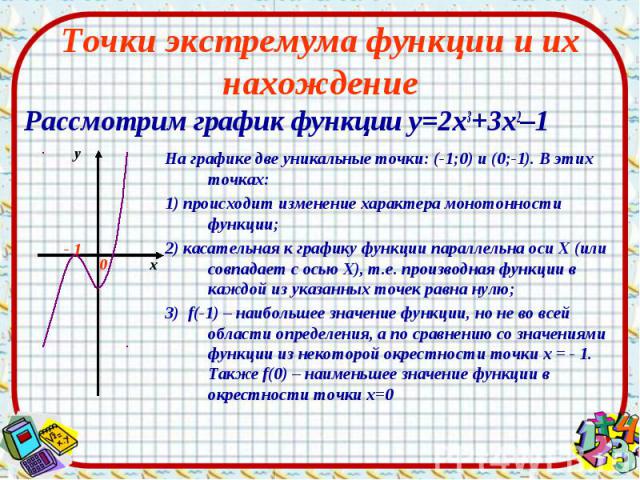
Точки экстремума функции и их нахождение Рассмотрим график функции у=2х3+3х2–1

Определение 1. Точку х=х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой (кроме самой точки х=х0) выполняется неравенство Определение 1. Точку х=х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой (кроме самой точки х=х0) выполняется неравенство f(х)>f(х0).

Значение максимума и минимума обозначаются: уmax , ymin соответственно. ВНИМАНИЕ!!! Только не путать с наибольшим (или наименьшим) значением функции во всей рассматриваемой области определения, эти значения в окрестности некоторой точки Х, являются наибольшими (или наименьшими).

Теорема 4. Если функция у = f(х) имеет экстремум в точке х=х0, то этой точке производная либо равна нулю, либо не существует. Теорема 4. Если функция у = f(х) имеет экстремум в точке х=х0, то этой точке производная либо равна нулю, либо не существует.

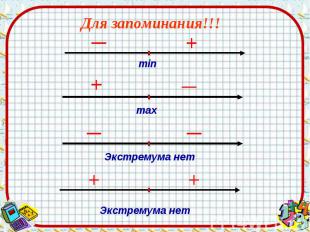
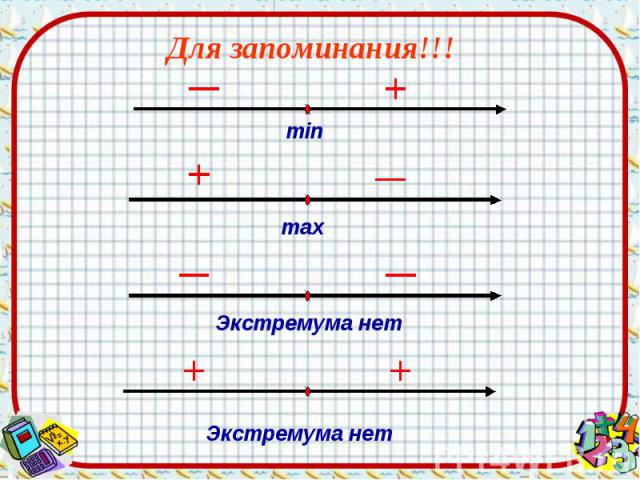
Для запоминания!!!

Пример:Найти точки экстремума функции у=3х4 – 16х3 + 24х2 – 11. Решение: найдем производную данной функции: у1=12х3 – 48х2 + 48х.

Алгоритм исследования непрерывной функции у=f(х) на монотонность и экстремумы: Алгоритм исследования непрерывной функции у=f(х) на монотонность и экстремумы: Найти производную f1(х). Найти стационарные (f1(х)=0) и критические (f1(х) не существует) точки функции у=f(х). Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках. На основании теорем 1, 2, и 5 сделать выводы о монотонности функции и о ее точках экстремума.

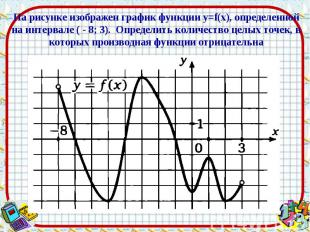
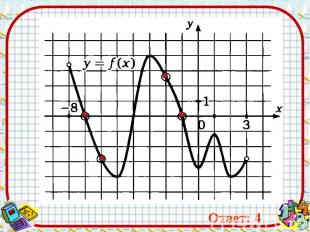
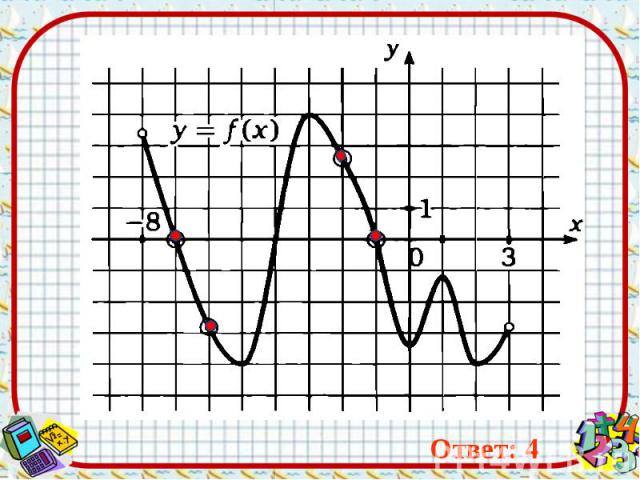
Ответ: 4 Ответ: 4

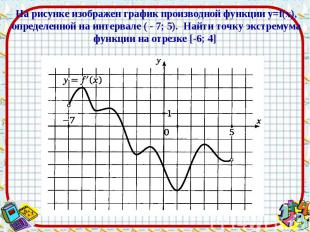
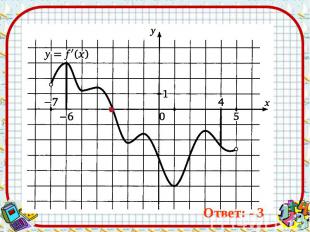
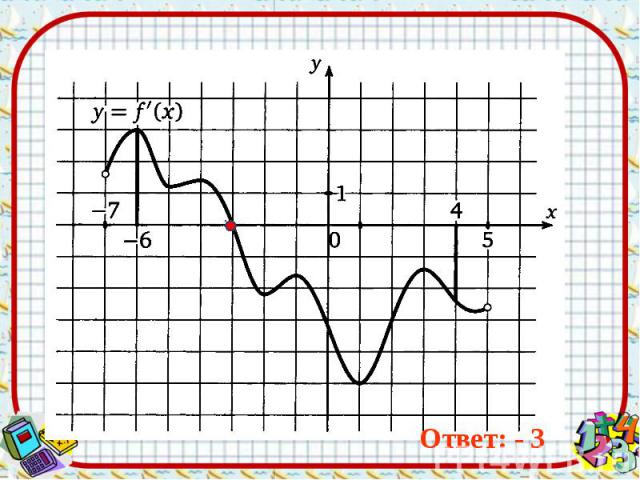
Ответ: - 3 Ответ: - 3

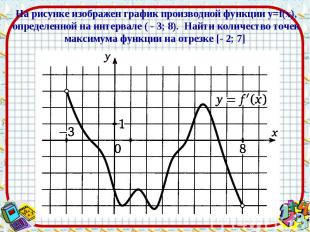
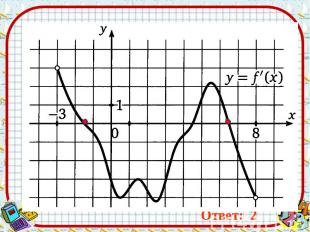
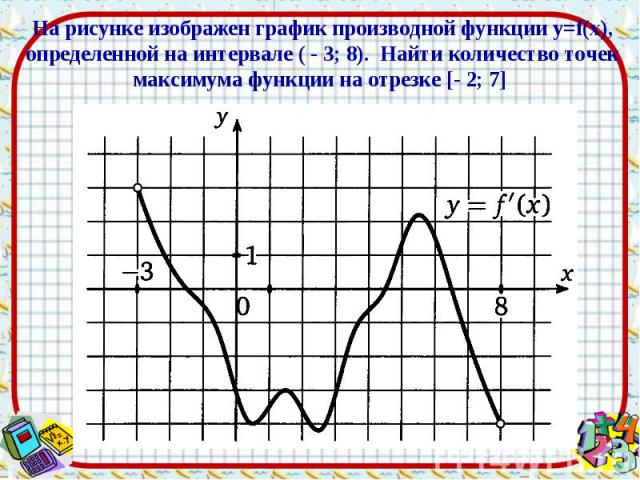
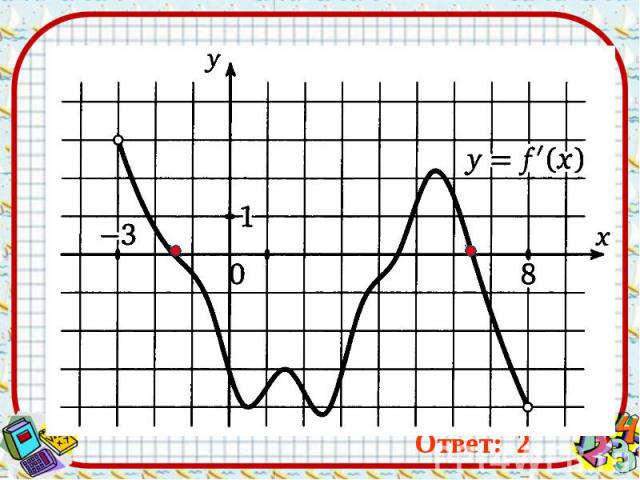
Ответ: 2 Ответ: 2

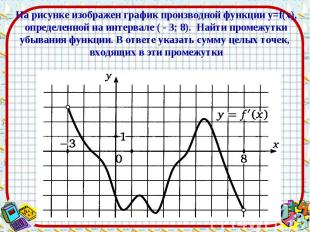
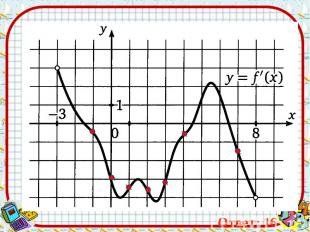
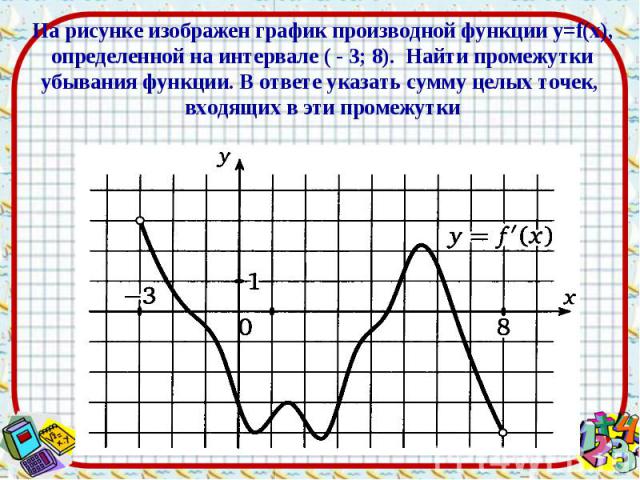
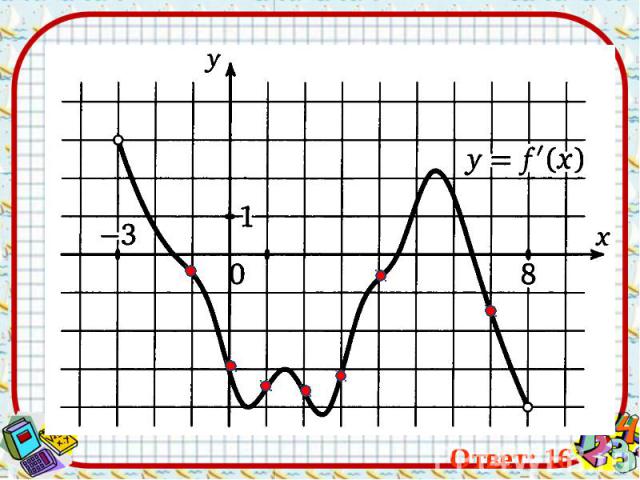
Ответ: 16 Ответ: 16

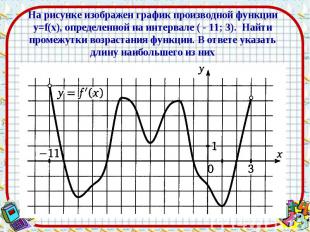
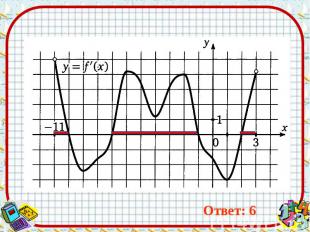
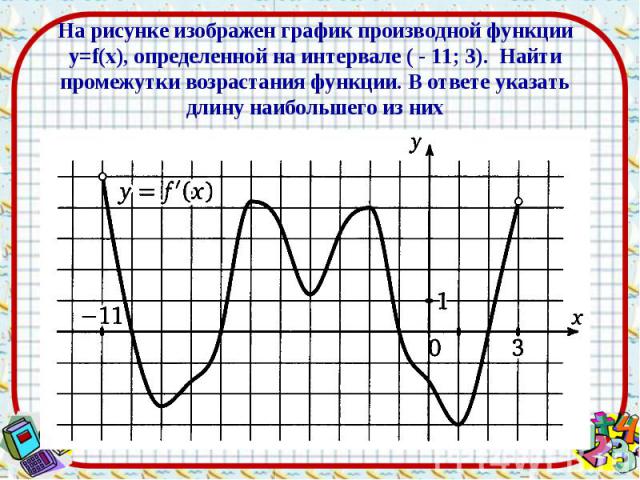
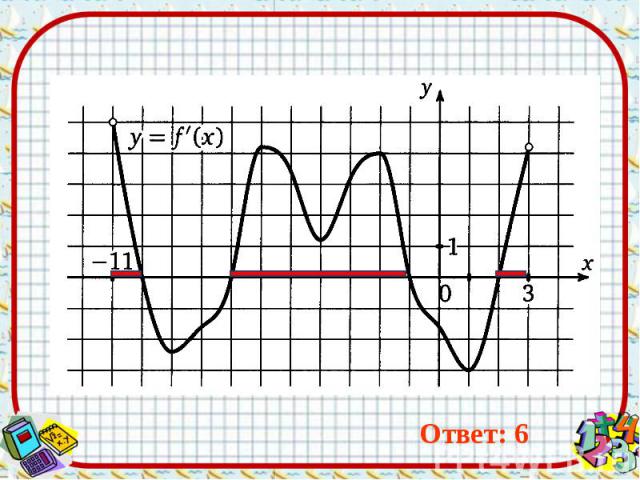
Ответ: 6 Ответ: 6

Работа с учебником: №30.12, 30.13, 30.26

http://i.allday.ru/uploads/posts/2009-08/thumbs/1250058141_12.jpg http://i.allday.ru/uploads/posts/2009-08/thumbs/1250058141_12.jpg http://www.ccboe.net/Teachers/Durham_Sharon/images/918F9422010B4BB0B160956D6B9D4E34.JPG http://www.utkonos.ru/images/it/027/008/006/1238197P.jpg http://www.caringbahlearningcentre.com.au/assets/images/calc.JPG