Презентация на тему: Тригонометрия. Тригонометрические уравнения.

Тригонометрические уравнения

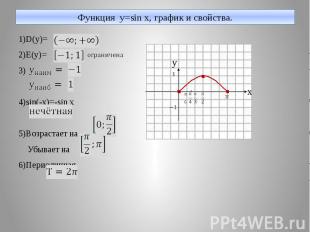
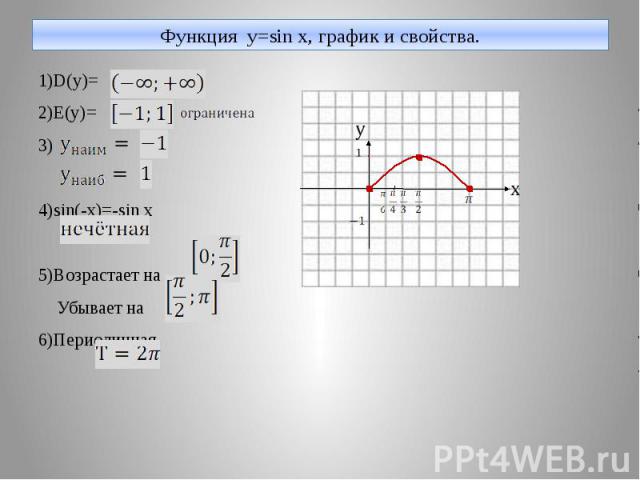
Функция y=sin x, график и свойства. 1)D(y)= 2)E(y)= 3) 4)sin(-x)=-sin x 5)Возрастает на Убывает на 6)Периодичная

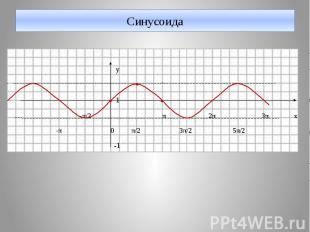
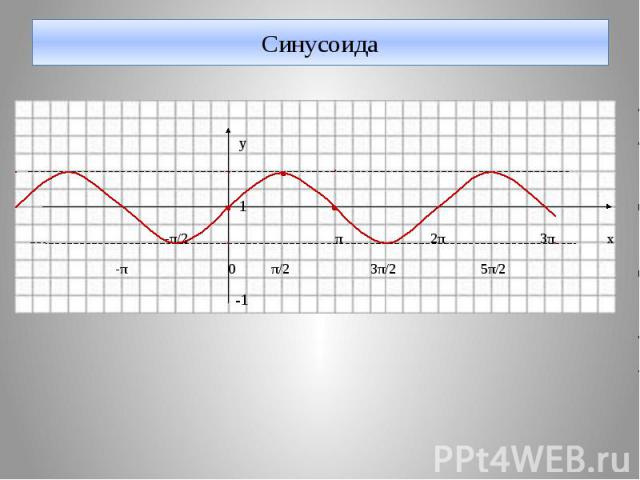
Синусоида у 1 -π/2 π 2π 3π х -π 0 π/2 3π/2 5π/2 -1

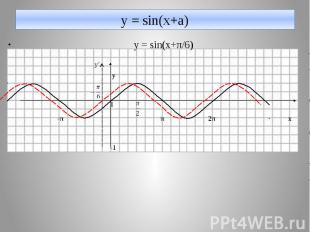
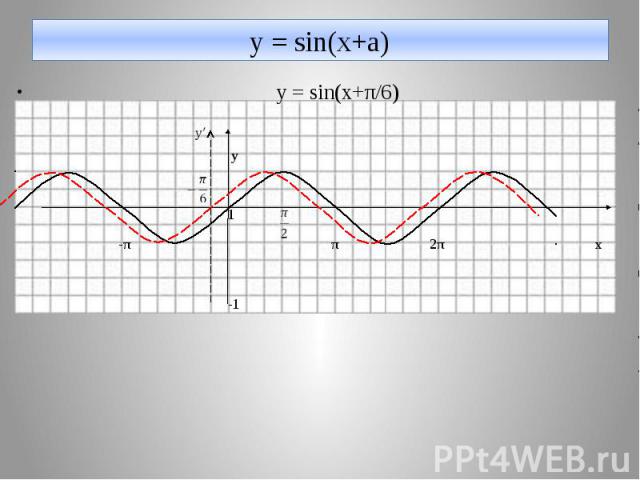
у = sin(x+a) y = sin(x+π/6) y 1 -π π 2π х -1

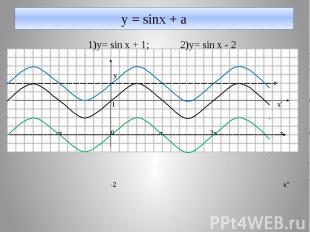
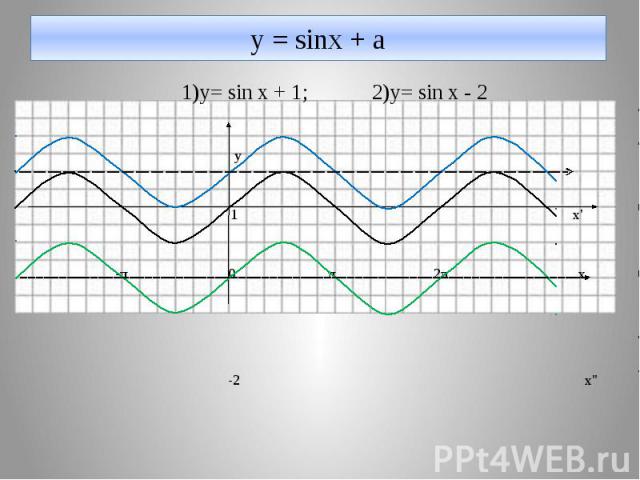
у = sinx + a 1)y= sin x + 1; 2)y= sin x - 2 y 1 x' -π 0 π 2π x -2 x''

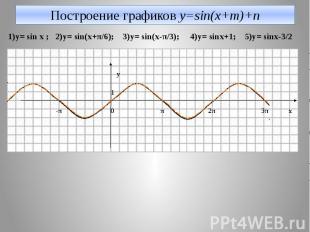
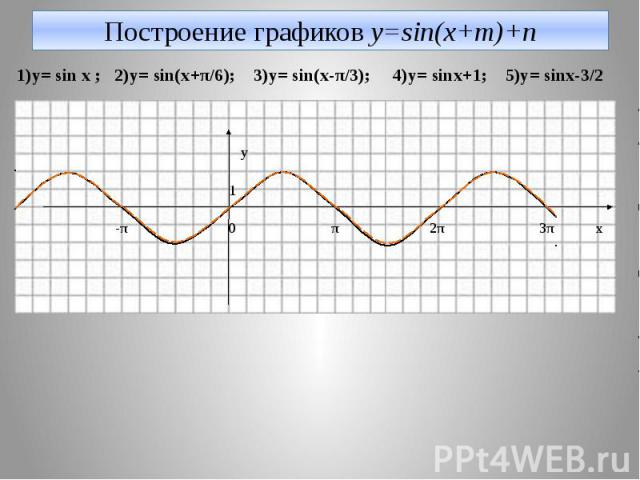
Построение графиков y=sin(x+m)+n 1)y= sin x ; 2)y= sin(x+π/6); 3)y= sin(x-π/3); 4)y= sinx+1; 5)y= sinx-3/2 y 1 -π 0 π 2π 3π x

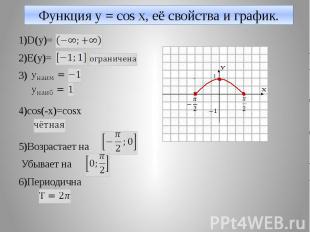
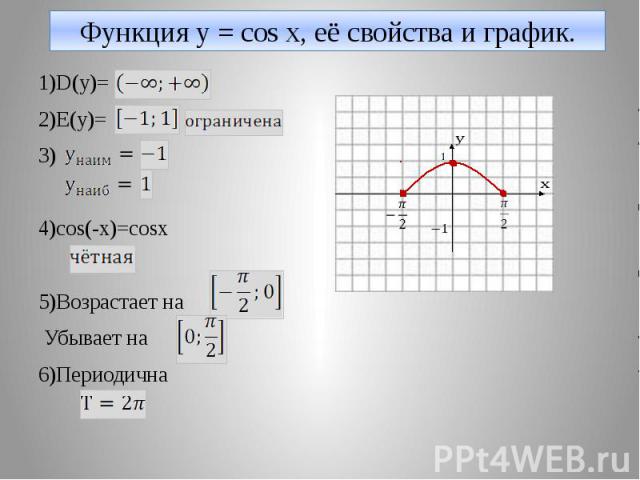
Функция y = cos x, её свойства и график. 1)D(y)= 2)E(y)= 3) 4)cos(-x)=cosx 5)Возрастает на Убывает на 6)Периодична

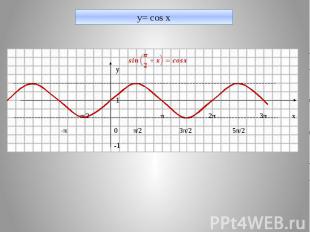
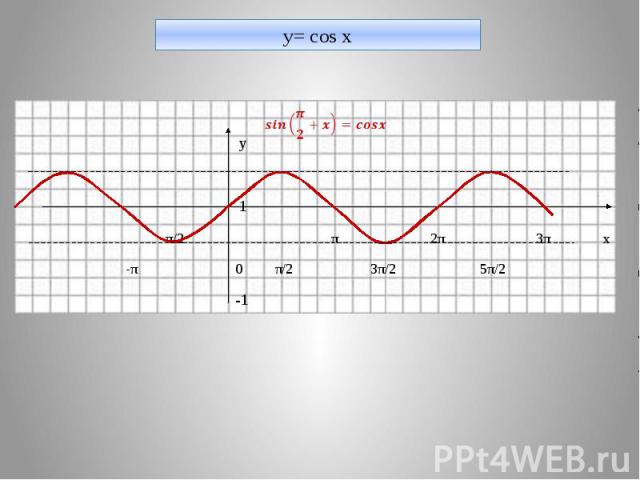
y= cos x у 1 -π/2 π 2π 3π х -π 0 π/2 3π/2 5π/2 -1

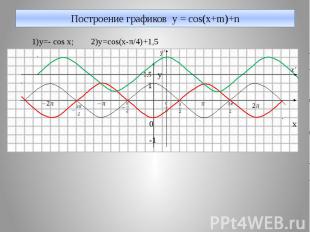
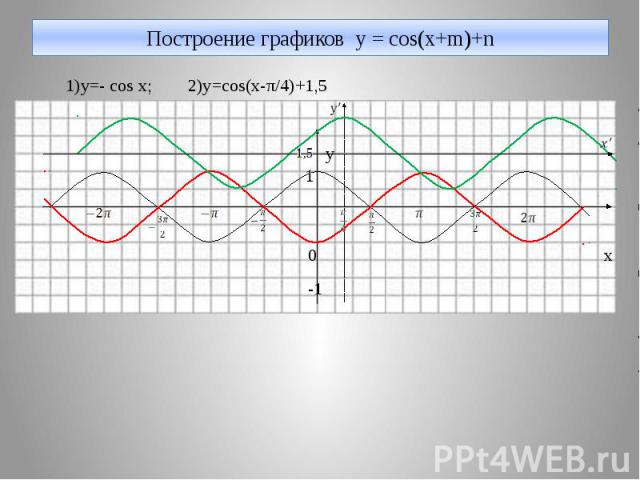
Построение графиков y = cos(x+m)+n 1)y=- cos x; 2)y=cos(x-π/4)+1,5 y 0 x -1

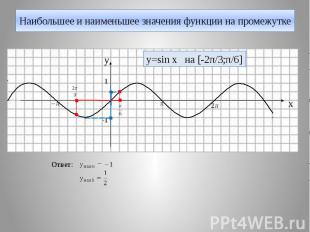
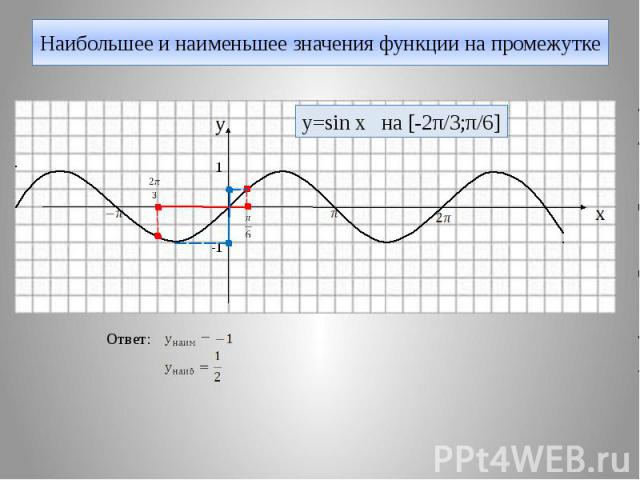
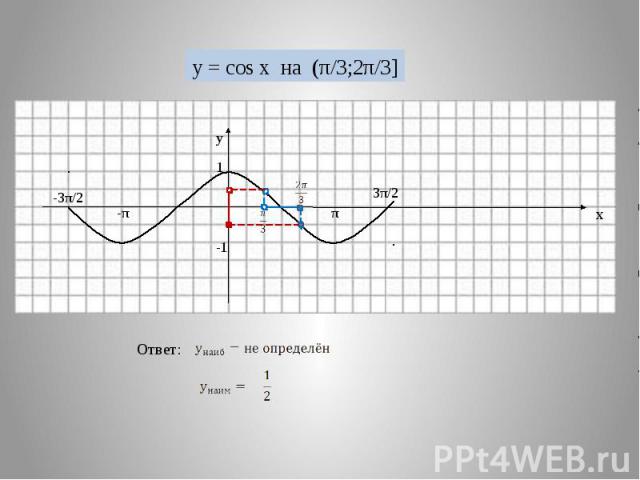
Наибольшее и наименьшее значения функции на промежутке

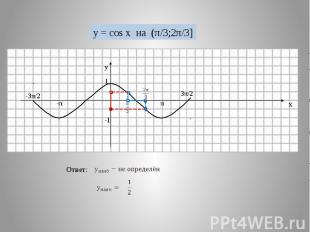
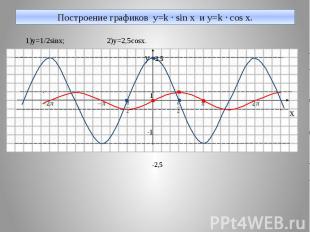
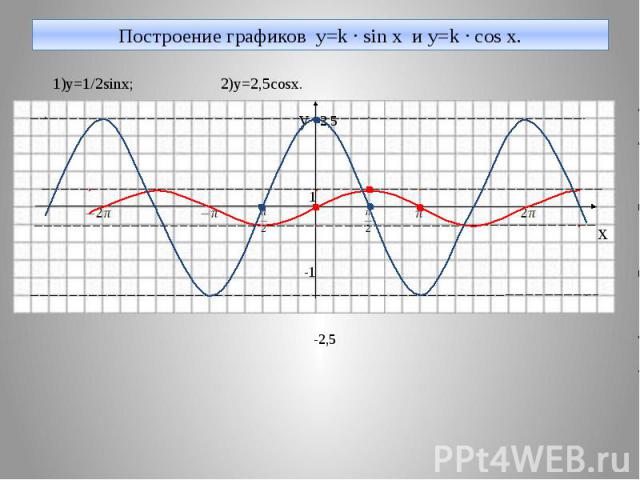
Построение графиков y=k · sin x и y=k · cos x. 1)y=1/2sinx; 2)y=2,5cosx. y 2,5 1 x -1 -2,5

Множество значений функции Пример: y=-9cos(x+π/6)-0,5 -1≤ cosx ≤1 -1≤ cos(x+π/6) ≤1 -9≤ -9cos(x+π/6) ≤9 -9,5≤ -9cos(x+π/6)-0,5 ≤8,5 yЄ[-9,5;8,5] 1)y=sinx-3; 2)y= cos(x+π/3); 3)y=sin(-2x+π)+1; 4)y=5cosx; 5)y= -sinx; 6)y=1/2cosx-3; 7)y=-4sin(x+1)+7; 8)y= cosx- ; 9)y=-1-sin .

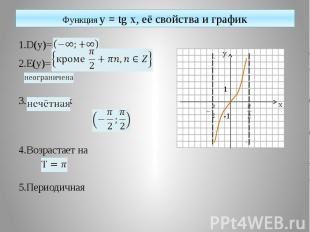
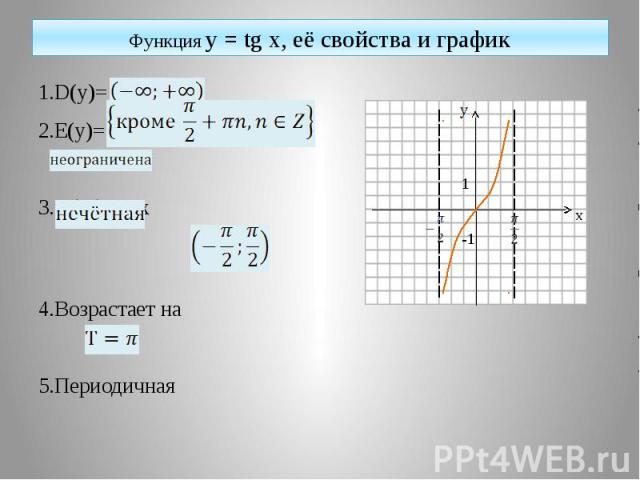
Функция y = tg x, её свойства и график 1.D(y)= 2.E(y)= 3.tg(-x)=-tgx 4.Возрастает на 5.Периодичная

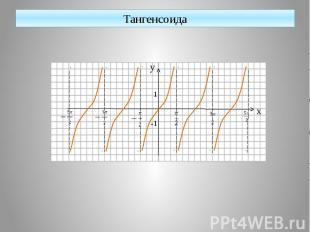
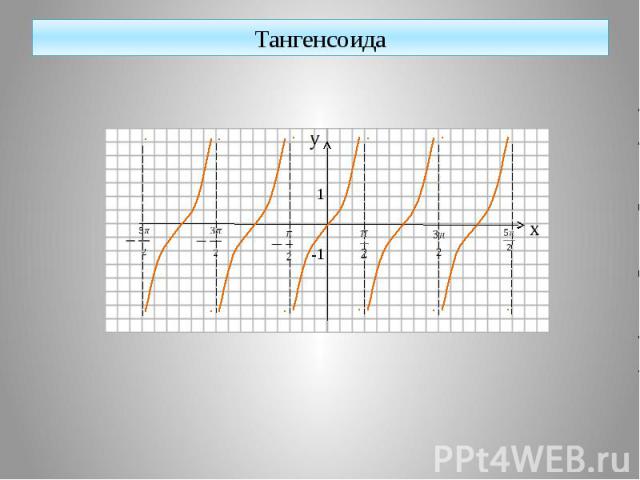
Тангенсоида

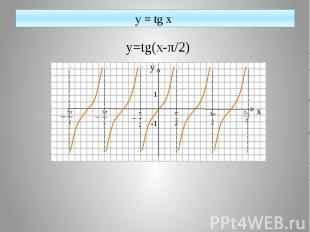
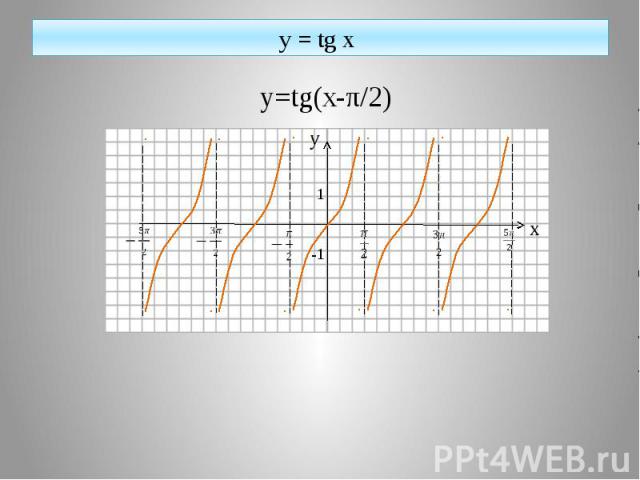
y = tg x y=tg(x-π/2)

Периодичность 1)x; x+T; x-TЄD(f) 2) Если y=f(x) периодичная с периодом Т₁‡0, то y=A· f(kx+m)+B периодичная с периодом Примеры: 1) 2)

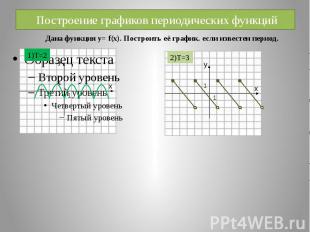
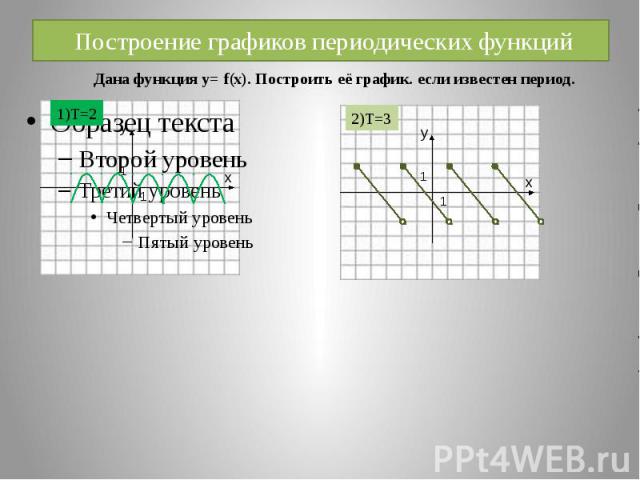
Построение графиков периодических функций

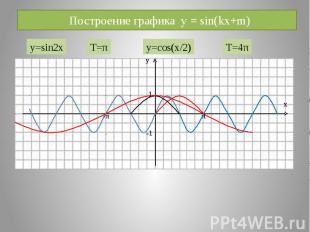
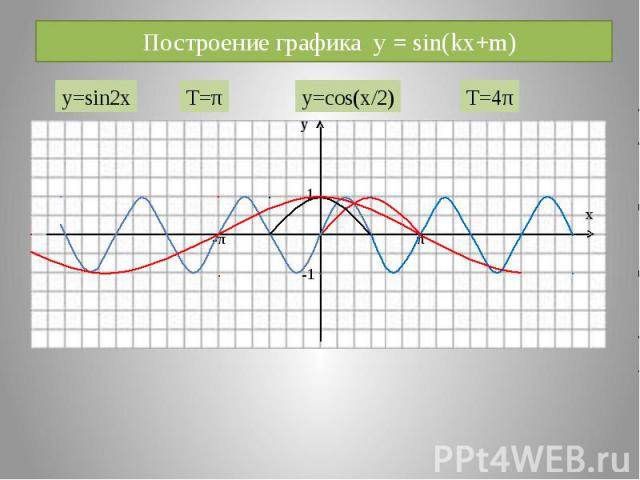
Построение графика y = sin(kx+m)

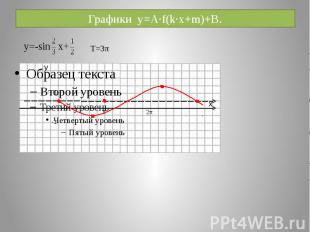
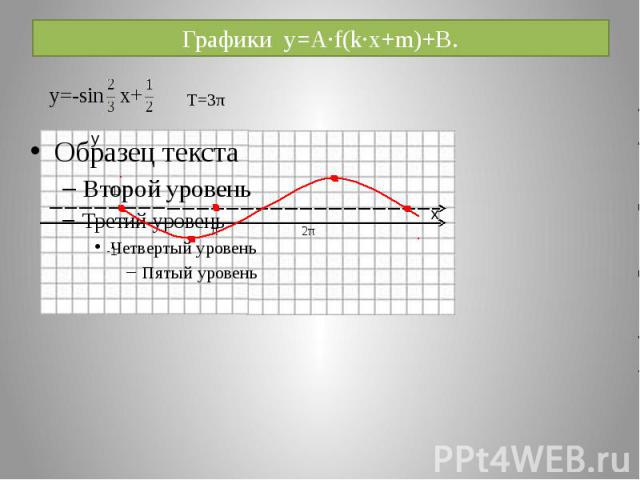
Графики y=A·f(k·x+m)+B.

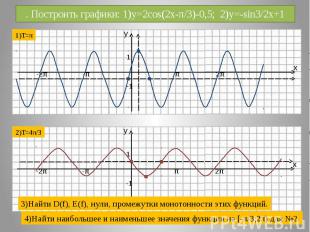
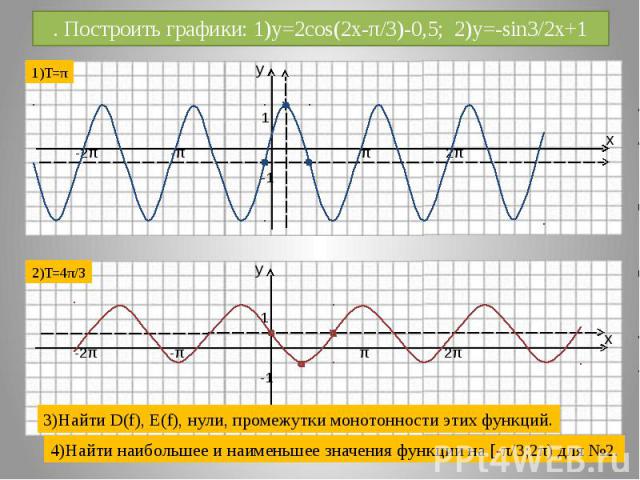
. Построить графики: 1)y=2cos(2x-π/3)-0,5; 2)y=-sin3/2x+1