Презентация на тему: Тригонометрия

Тригонометрия Числовая окружность. Формулы. Попкова Т.Г. МОУ СОШ № 2 Горячий Ключ

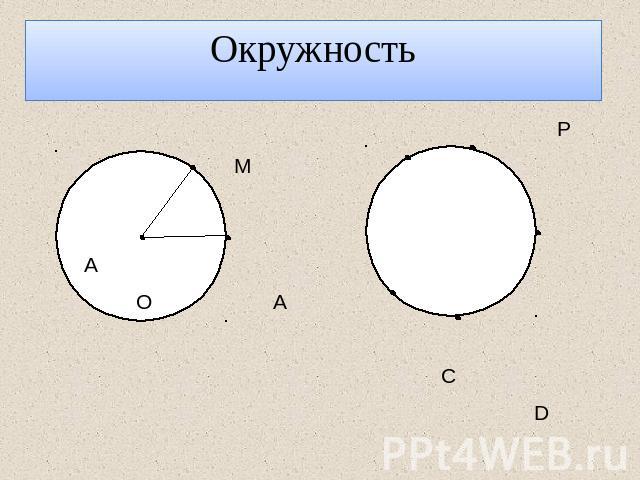
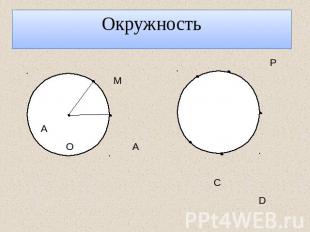
Окружность

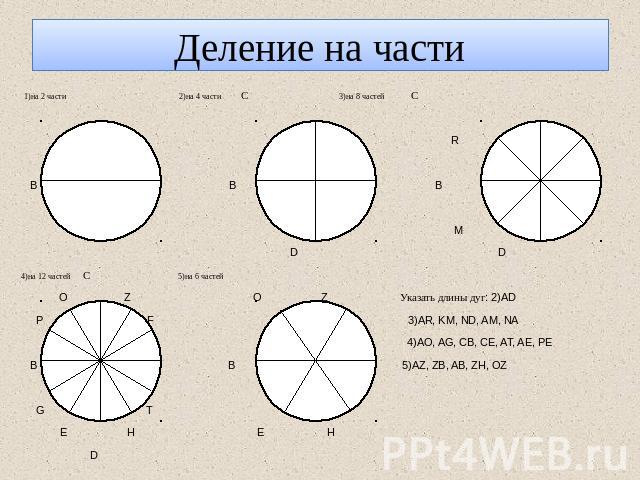
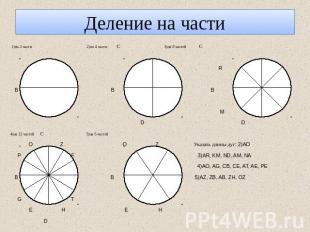
Деление на части

Отметить на числовой окружности точки М( t) такие, что:

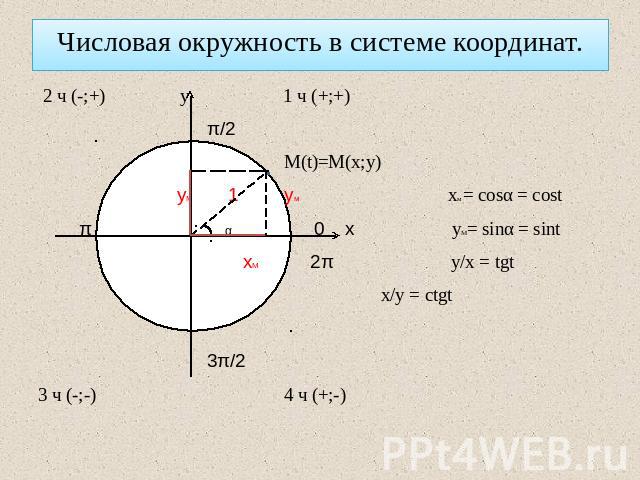
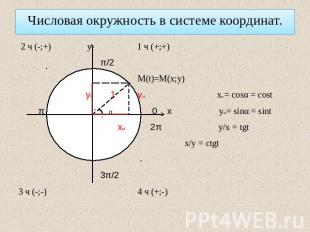
Числовая окружность в системе координат.

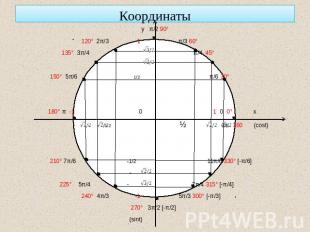
Координаты

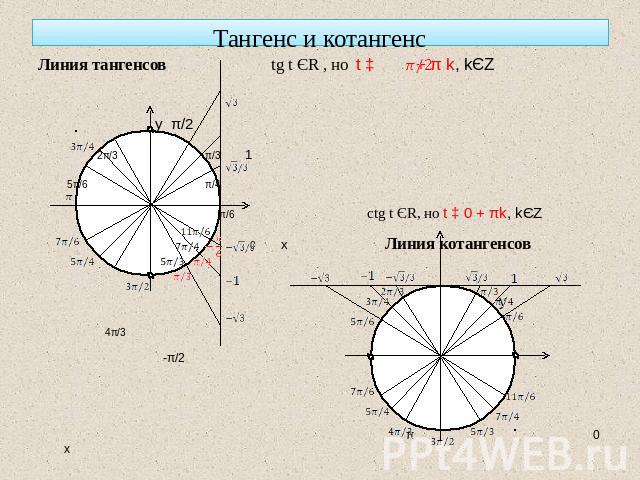
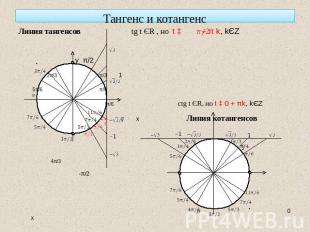
Тангенс и котангенс

Знаки и значения

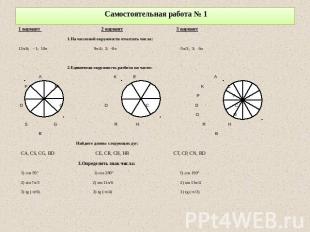
Самостоятельная работа № 1

Работа с формулами

Основные тригонометрические тождества

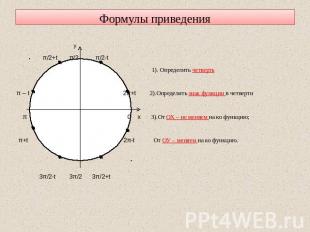
Формулы приведения

Формулы сложения 1.sin(x + y)= sinx·cosy + siny·cosx 2.cos(x + y)= cosx·cosy - sinx·siny 3.sin(x – y)= sinx·cosy - siny·cosx 4.cos(x – y)= cosx·cosy + sinx·siny

Формулы двойного и половинного аргумента 1.sin2x = 2 sinx·cosx; 2.cos2x = cos²x - sin²x; 3.cos2x = 1 – 2sin²x; 4.cos2x = 2cos²x-1;

Преобразование сумм тригонометрических функций в произведение