Презентация на тему: Понятие цилиндра

Понятие цилиндра. МОУ СОШ №256 г.Фокино

Цилиндры вокруг нас.

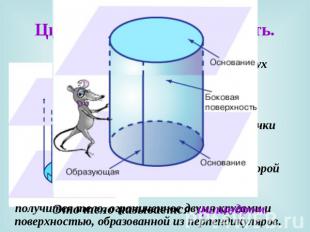
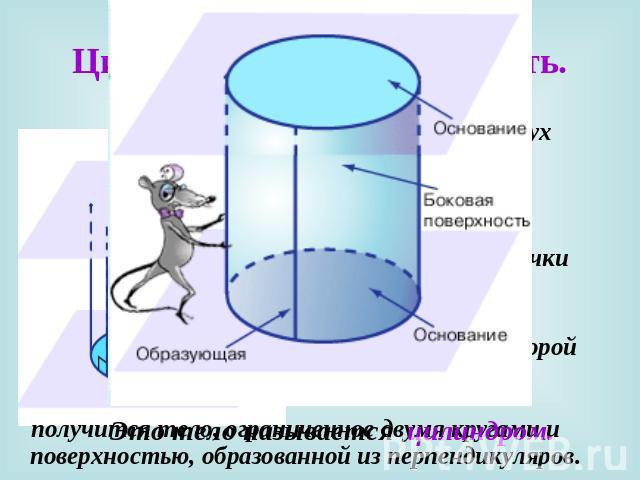
Цилиндрическая поверхность. Если в одной из двух параллельных плоскостей взять окружность, и из каждой ее точки восстановить перпендикуляр до пересечения со второй плоскостью, то Это тело называется цилиндром. получится тело, ограниченное двумя кругами и поверхностью, образованной из перпендикуляров.

Точное название определенного выше тела – прямой круговой цилиндр. Вообще, цилиндр возникает при пересечении цилиндрической поверхности, образованной множеством параллельных прямых, проведенных через каждую точку замкнутой кривой линии, и двух параллельных плоскостей.

Цилиндры бывают прямыми и наклонными в зависимости от того перпендикулярны или наклонны плоскости оснований к образующим. В основаниях могут лежать различные фигуры.

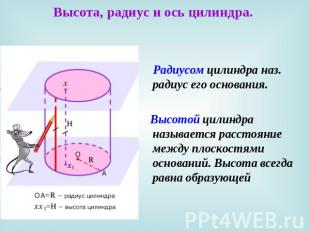
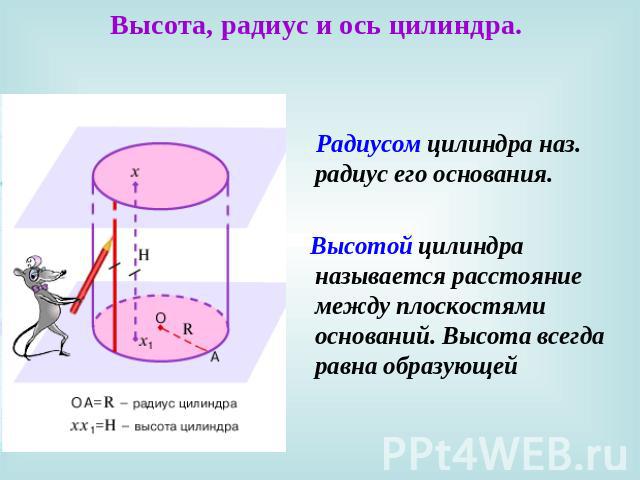
Высота, радиус и ось цилиндра. Радиусом цилиндра наз. радиус его основания. Высотой цилиндра называется расстояние между плоскостями оснований. Высота всегда равна образующей

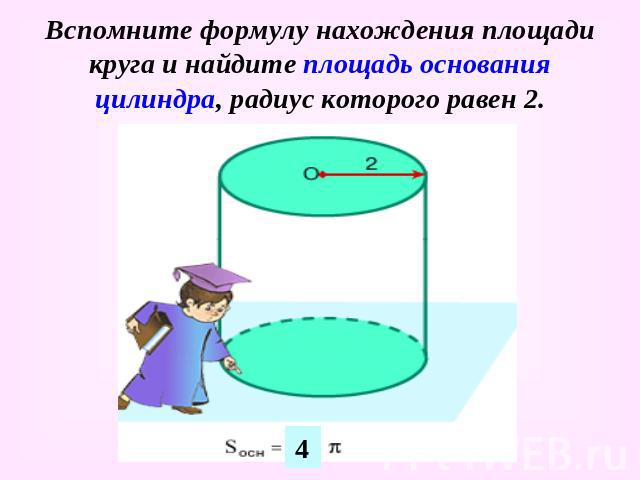
Вспомните формулу нахождения площади круга и найдите площадь основания цилиндра, радиус которого равен 2.

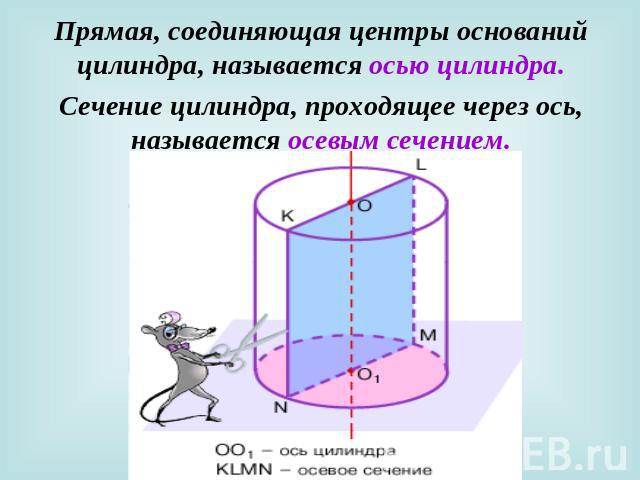
Прямая, соединяющая центры оснований цилиндра, называется осью цилиндра. Сечение цилиндра, проходящее через ось, называется осевым сечением.

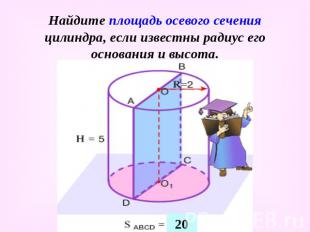
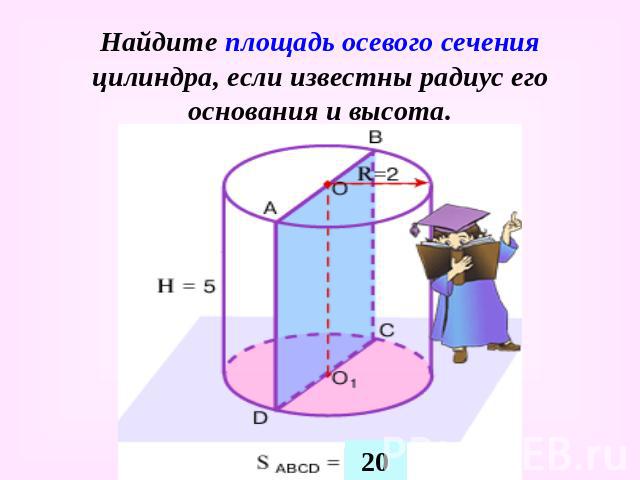
Найдите площадь осевого сечения цилиндра, если известны радиус его основания и высота.

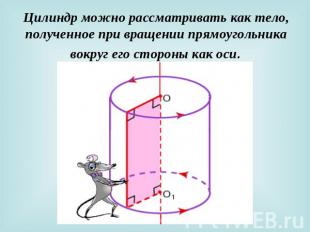
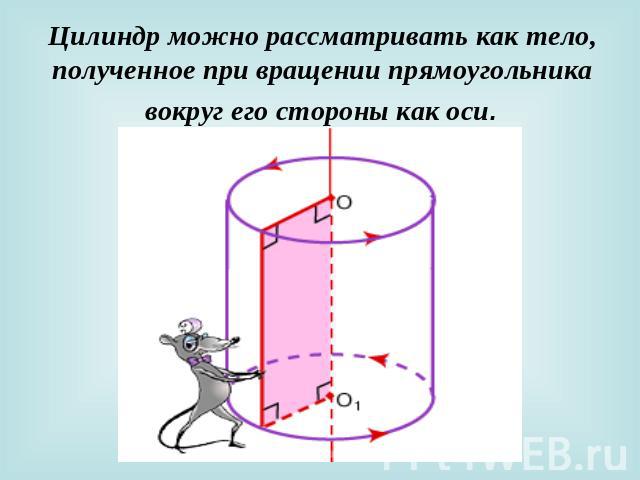
Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси.

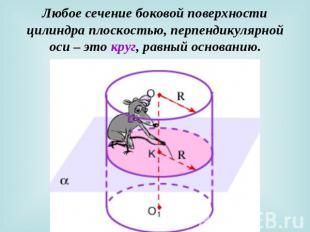
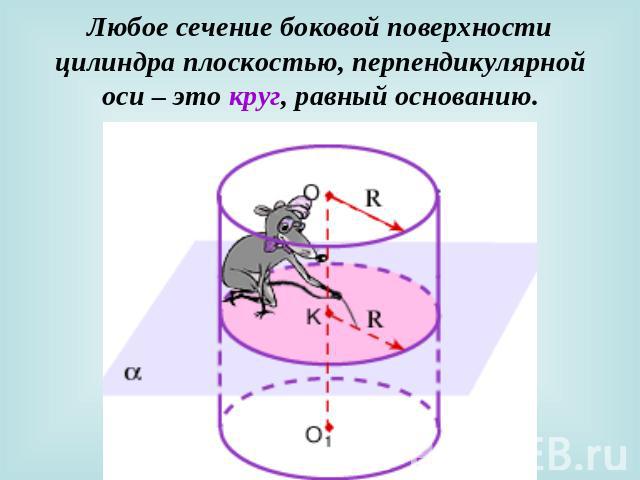
Любое сечение боковой поверхности цилиндра плоскостью, перпендикулярной оси – это круг, равный основанию.

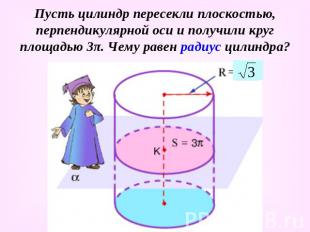
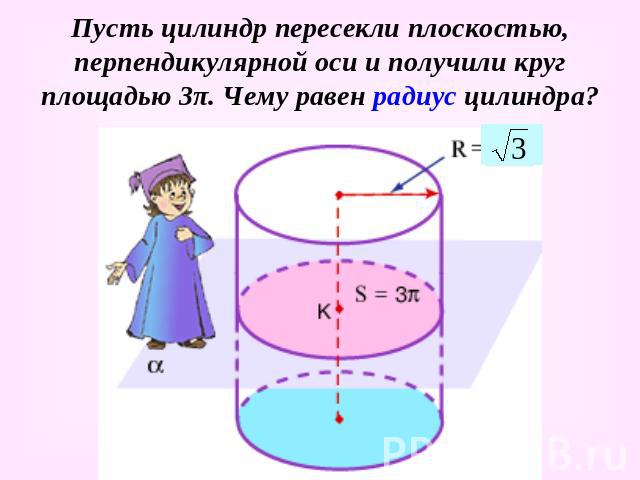
Пусть цилиндр пересекли плоскостью, перпендикулярной оси и получили круг площадью 3π. Чему равен радиус цилиндра?

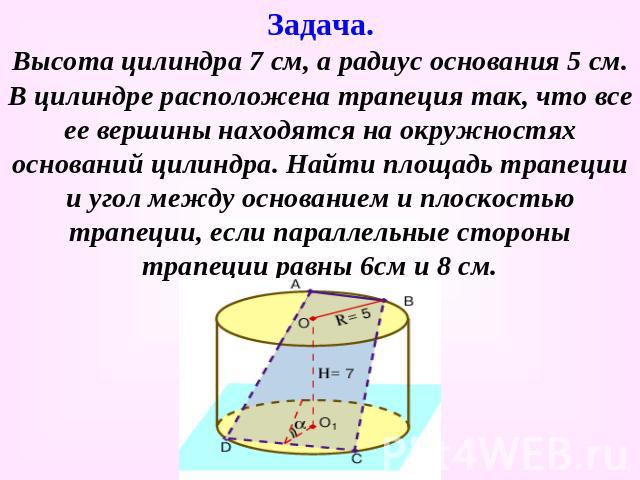
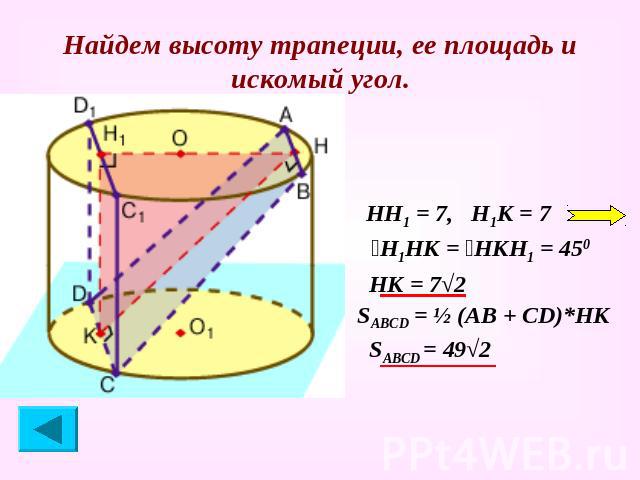
Высота цилиндра 7 см, а радиус основания 5 см. В цилиндре расположена трапеция так, что все ее вершины находятся на окружностях оснований цилиндра. Найти площадь трапеции и угол между основанием и плоскостью трапеции, если параллельные стороны трапеции равны 6см и 8 см. Задача.

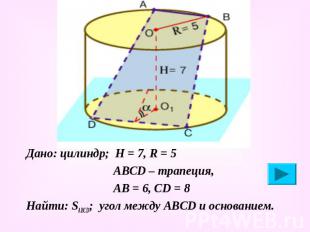
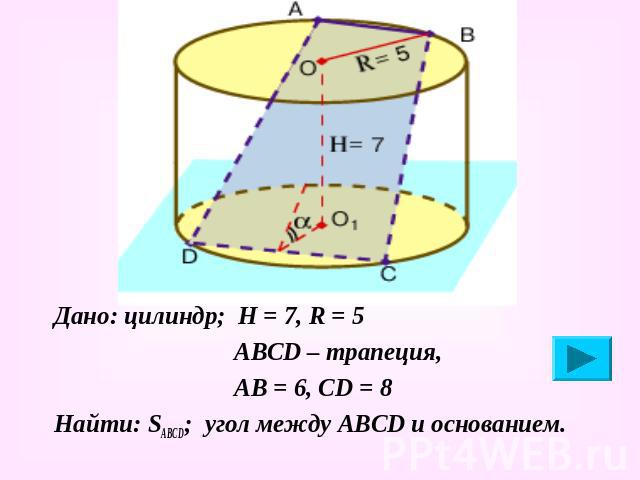
Дано: цилиндр; Н = 7, R = 5 Дано: цилиндр; Н = 7, R = 5 АВСD – трапеция, АВ = 6, СD = 8 Найти: SABCD; угол между АВСD и основанием.

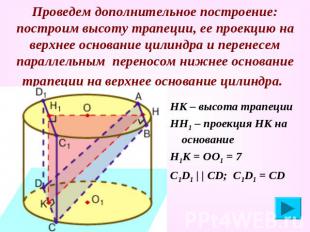
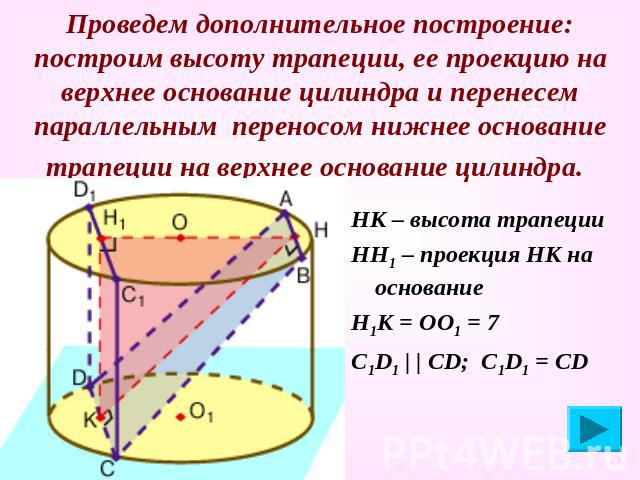
Проведем дополнительное построение: построим высоту трапеции, ее проекцию на верхнее основание цилиндра и перенесем параллельным переносом нижнее основание трапеции на верхнее основание цилиндра. НК – высота трапеции НН1 – проекция НК на основание Н1К = ОО1 = 7 С1D1 | | СD; С1D1 = CD

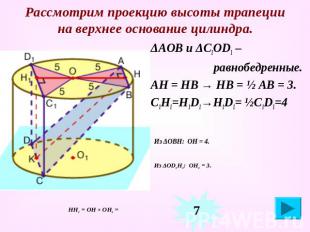
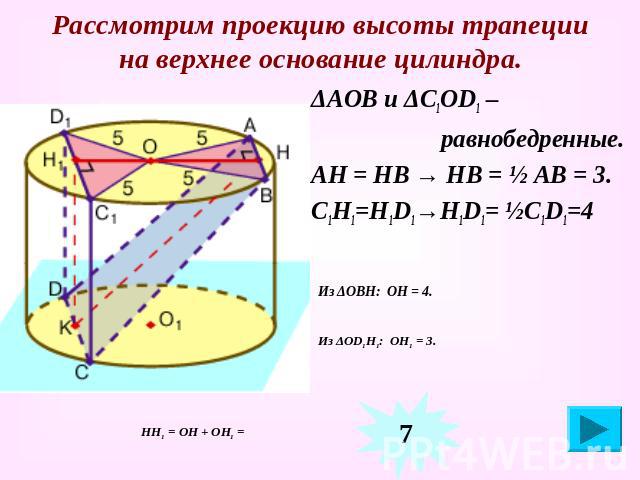
Рассмотрим проекцию высоты трапеции на верхнее основание цилиндра. ΔАОВ и ΔС1ОD1 – равнобедренные. АН = НВ → НВ = ½ АВ = 3. С1Н1=Н1D1→Н1D1= ½С1D1=4

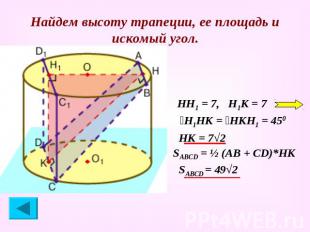
Найдем высоту трапеции, ее площадь и искомый угол. НН1 = 7, Н1К = 7 ےН1НК = ےНКН1 = 450 НК = 7√2 SABCD = ½ (АВ + СD)*НК SАВСD = 49√2

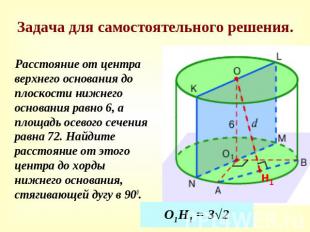
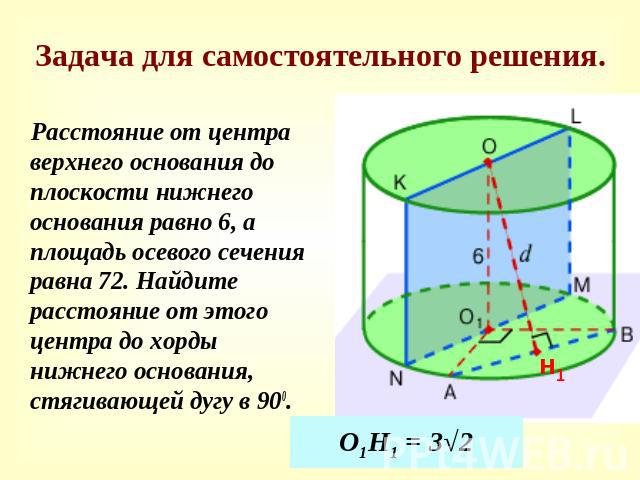
Задача для самостоятельного решения. Расстояние от центра верхнего основания до плоскости нижнего основания равно 6, а площадь осевого сечения равна 72. Найдите расстояние от этого центра до хорды нижнего основания, стягивающей дугу в 900.

Домашнее задание: П. 53, 54 №№ 523, 525, 529. Спасибо за урок!