Презентация на тему: Симметрия в пространстве

СИММЕТРИЯ В ПРОСТРАНСТВЕ. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ.

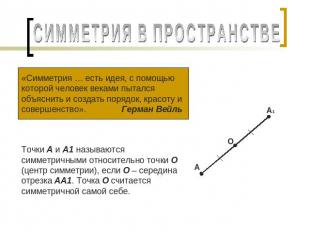
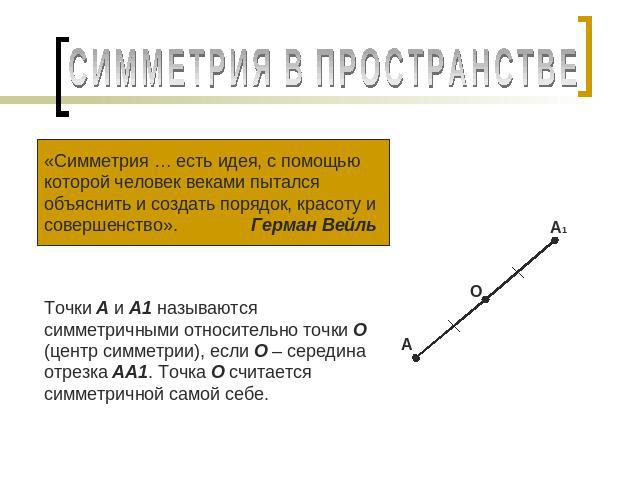
СИММЕТРИЯ В ПРОСТРАНСТВЕ «Симметрия … есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство». Герман Вейль Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1. Точка О считается симметричной самой себе.

СИММЕТРИЯ В ПРОСТРАНСТВЕ Точки А и А1 называются симметричными относительно прямой (ось симметрии), если прямая проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка прямой а считается симметричной самой себе. Лист, снежинка, бабочка – примеры осевой симметрии.

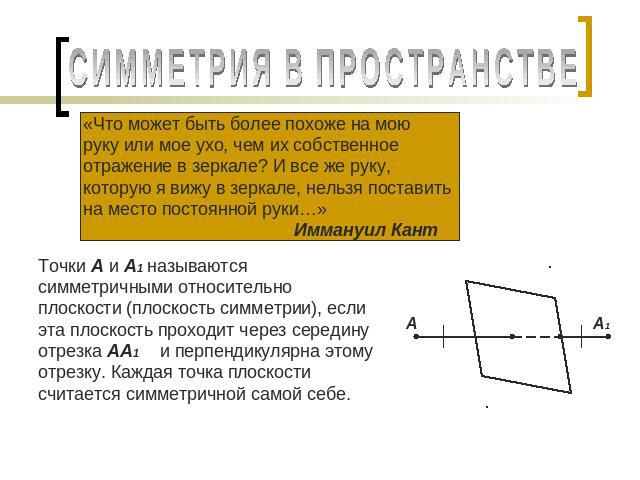
СИММЕТРИЯ В ПРОСТРАНСТВЕ «Что может быть более похоже на мою руку или мое ухо, чем их собственное отражение в зеркале? И все же руку, которую я вижу в зеркале, нельзя поставить на место постоянной руки…» Иммануил Кант Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если эта плоскость проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка плоскости считается симметричной самой себе.

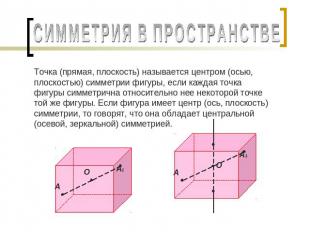
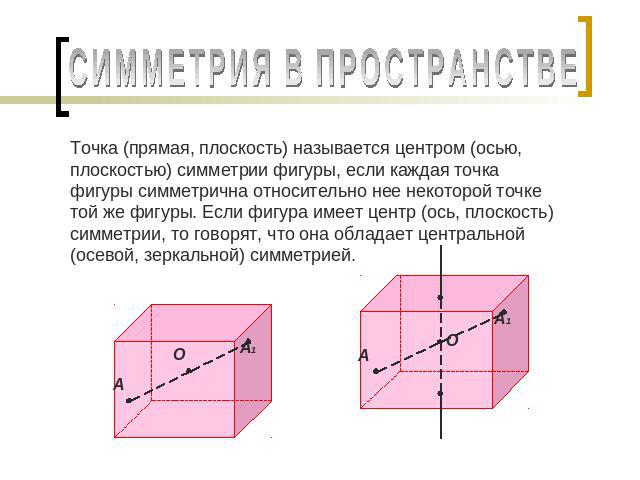
СИММЕТРИЯ В ПРОСТРАНСТВЕ Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.

СИММЕТРИЯ В ПРИРОДЕ «Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни есть симметрия?» Л. Толстой «Отрочество» Кристалл аметиста Кристаллы льда

СИММЕТРИЯ В ИСКУССТВЕ Церковь Покрова Богородицы на Нерли

СИММЕТРИЯ В ИСКУССТВЕ Кижи. Слева церковь Преображения. 1714 г.

СИММЕТРИЯ В ИСКУССТВЕ Здание МГУ

СИММЕТРИЯ В ИСКУССТВЕ Микеланджело. Гробница Джулиано Медичи

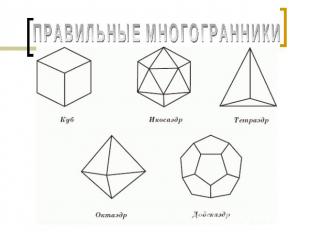
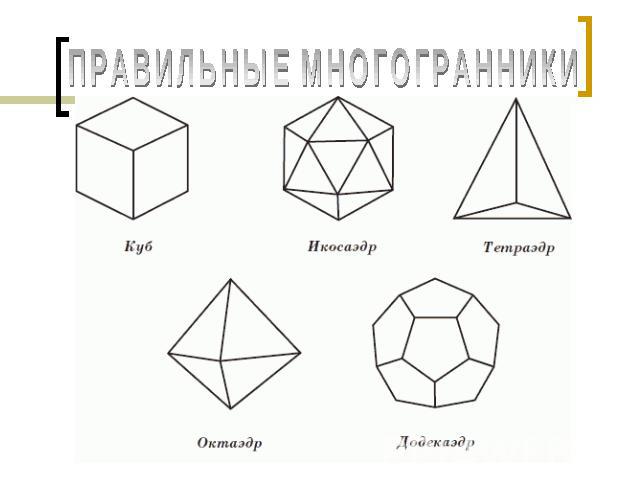
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

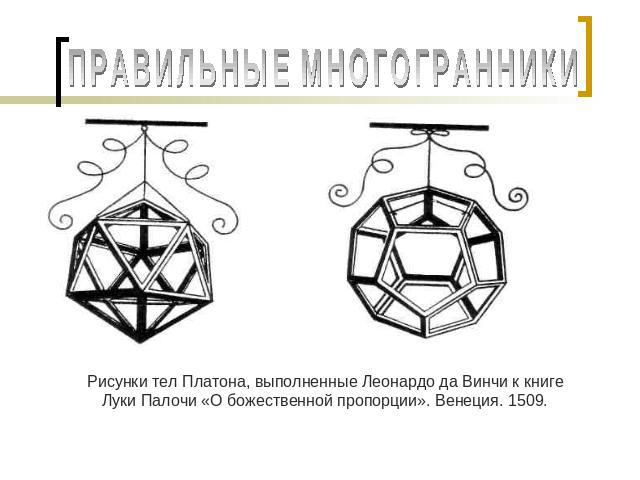
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Рисунки тел Платона, выполненные Леонардо да Винчи к книге Луки Палочи «О божественной пропорции». Венеция. 1509.

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ С. Дали. Тайная вечеря

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Дюрер. Меланхолия. Фрагмент гравюры на меди. 1514.

Автор: ОРКИНА МАРИНА АЛЕКСАНДРОВНА, преподаватель ГОУ СПО «Зубово-Полянский педагогический колледж» Республика Мордовия