Презентация на тему: Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильного многогранника

Тема урока «Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильного многогранника.» Дата создания 03.07.2006

Цель урока: Ознакомление с понятием симметрии в пространстве и с понятием правильного многогранника Задачи урока: Ввести понятие правильного многогранника, рассмотреть все пять видов правильных многогранников

Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические свойства. Древнегреческий ученый и философ Платон (IV–V в до н. э.) считал, что эти тела олицетворяют сущность природы. В своем диалоге «Тимей» Платон говорит, что атом огня имеет вид тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра. Ученики Платона продолжили его дело в изучении перечисленных тел. Поэтому эти многогранники называют платоновыми телами.

Доказать, что не существует правильного многогранника, у которого гранями являются правильные n-угольники при n≥6.Угол правильного многоугольника вычисляется по формуле αn = 1800(n – 2)/n. При каждой вершине многогранника не меньше 3 плоских углов, и их сумма должна быть меньше 360о. При n=3, когда гранями многогранника служат правильные треугольники, имеем: α3=60о, 60о•3=180о<360o, 60о•4=240о<360o, 60о•5= 300о<360o, 60о•6=360о. В соответствии с этим получаем правильные многогранники – тетраэдр, октаэдр, икосаэдр.

Если n=4, то есть грани многогранника – квадраты, α4=90о, 90о•3=270о<360o, 90o•4=360o. Поэтому, в этом случае получаем только один правильный многогранник – куб.

Если n=5, то есть грани многогранника – правильные пятиугольники, то α5=108о, 108о•3=324о<360o, 108o•4=432o>360o, и поэтому в этом случае также имеем только один правильный многогранник – додекаэдр. Если n≥6, то αn≥120o, αn•3≥360o, и, следовательно, не существует правильного многогранника, гранями которого служат правильные n-угольники при n≥6.

Правильный тетраэдр не имеет центра симметрии. Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость а, проходящая через ребро АВ перпендикулярно к противоположному ребру СВ правильного тетраэдра АВСВ, является плоскостью симметрии. Правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии.

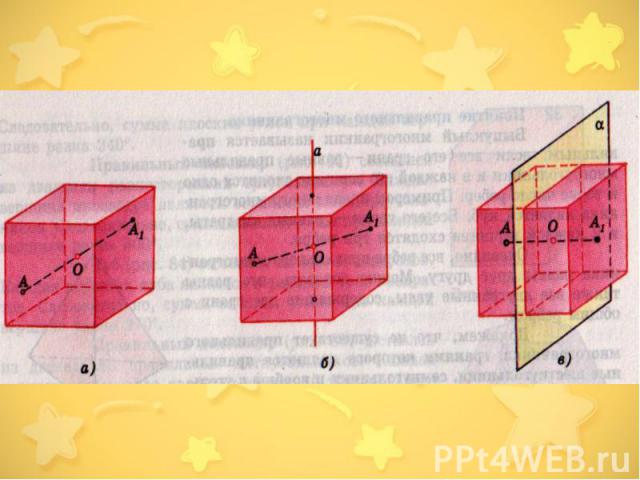
Куб имеет один центр симметрии — точку пересечения его диагоналей. Прямые а и Ь, проходящие соответственно через центры противоположных граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии. Куб имеет девять осей симметрии. Все оси симметрии проходят через центр симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Куб имеет девять плоскостей симметрии

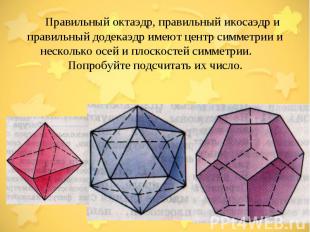
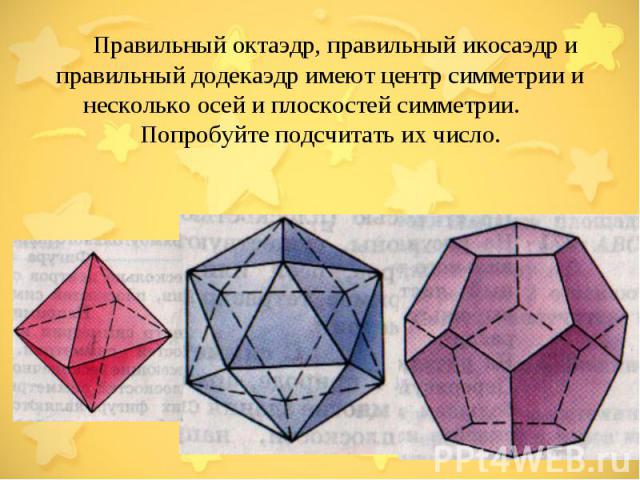
Правильный октаэдр, правильный икосаэдр и правильный додекаэдр имеют центр симметрии и несколько осей и плоскостей симметрии. Попробуйте подсчитать их число.

Решить задачи №276, 277, 278 (устно); №281, 282, 287.

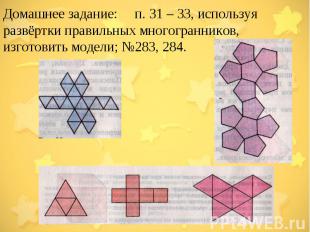
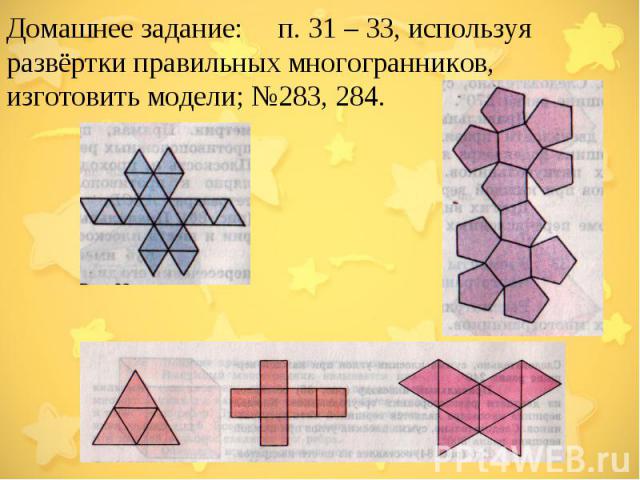
Домашнее задание:     п. 31 – 33, используя развёртки правильных многогранников, изготовить модели; №283, 284. 

Список использованной литературы:1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселёва Л.С., Позняк Э.Г. Геометрия 10-11, М.,«Просвещение» 2004г.2. Бутузов В.Ф., Саакян С.М. Изучение геометрии в 10-11 классах М.,«Просвещение» 2004г.3. ЦОР «Открытая математика 2.6 Стереометрия»