Презентация на тему: Метод параллельного проектирования. Изображение пространственных фигур на плоскости

Метод параллельного проектирования. Изображение пространственных фигур на плоскости. Геометрия, 10 класс.

Итак, мы приступили к изучению стереометрии – геометрии в пространстве. Как всегда нам необходимо уметь изображать геометрические фигуры, причем все чертежи мы по-прежнему выполняем на плоскости (на странице тетради, на доске и т.д.). Каким образом пространственную фигуру (например, куб) можно «уложить» в плоскость?

Выберем в пространстве произвольную плоскость (её мы будем называть плоскостью проекций) и любую прямую a (она задает направление параллельного проектирования).

Проведем через точку А прямую, параллельную прямой а. Точка А’ пересечения этой прямой с плоскостью и есть проекция точки А на плоскость . Точку А ещё называют прообразом, а точку А’ – образом. Если А, то А’ совпадает с А.

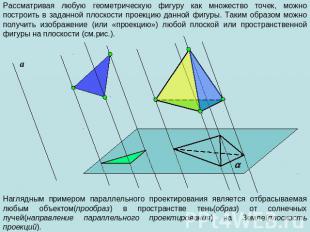
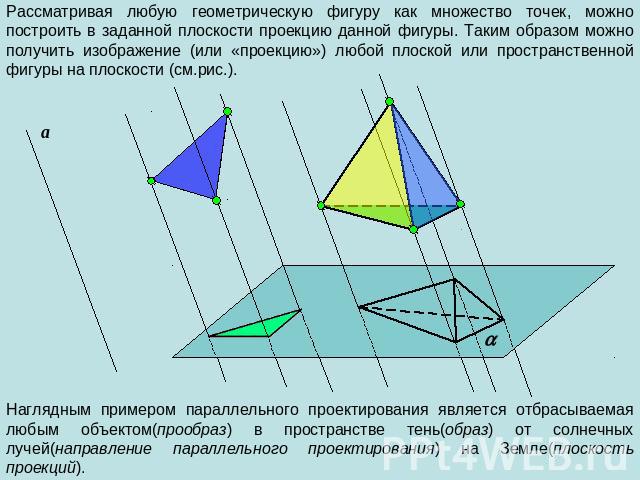
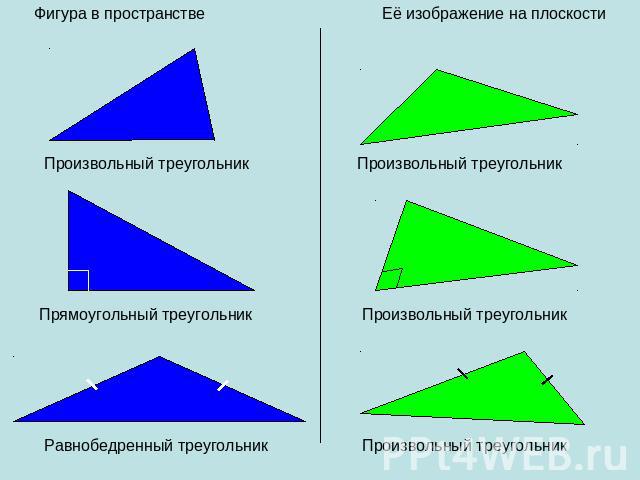
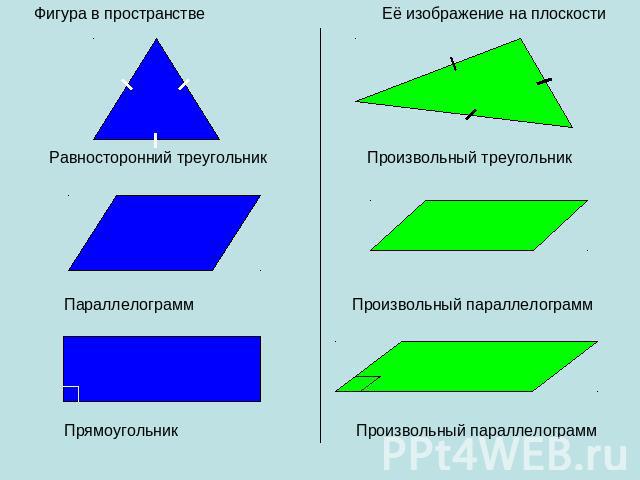
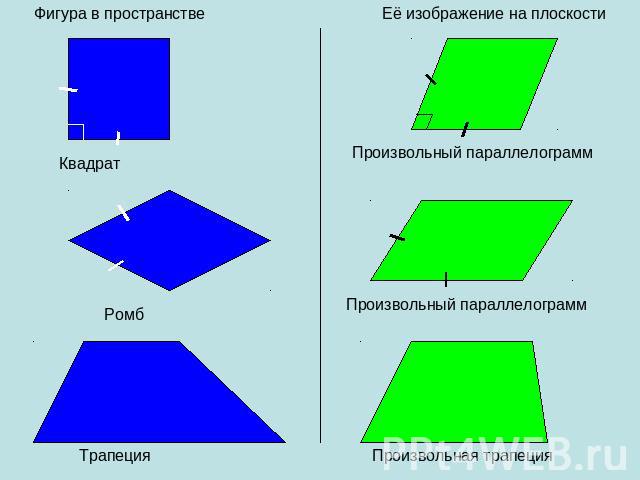
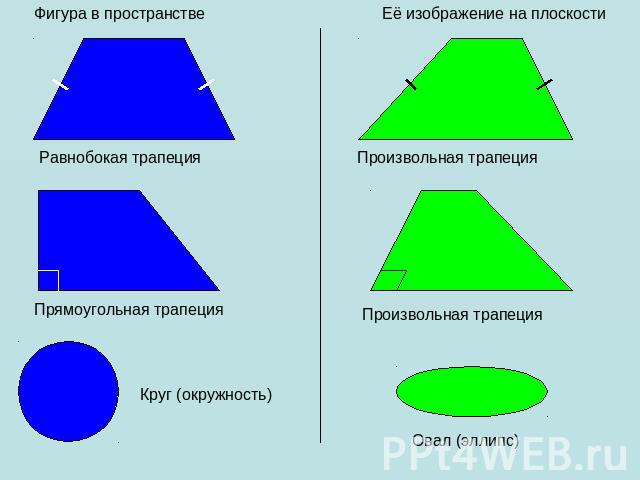
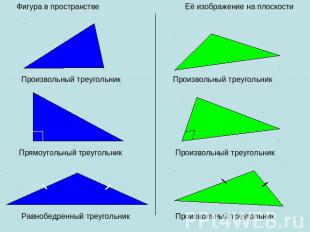
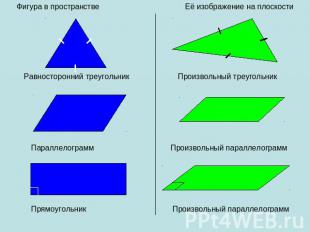
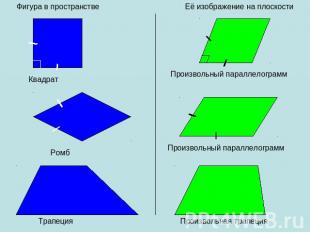
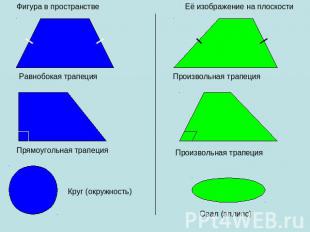
Рассматривая любую геометрическую фигуру как множество точек, можно построить в заданной плоскости проекцию данной фигуры. Таким образом можно получить изображение (или «проекцию») любой плоской или пространственной фигуры на плоскости (см.рис.). Наглядным примером параллельного проектирования является отбрасываемая любым объектом(прообраз) в пространстве тень(образ) от солнечных лучей(направление параллельного проектирования) на Земле(плоскость проекций).

Примечание 1. При параллельном проектировании не выбирают направление параллельного проектирования параллельно плоскости проекции (самостоятельно обоснуйте почему).

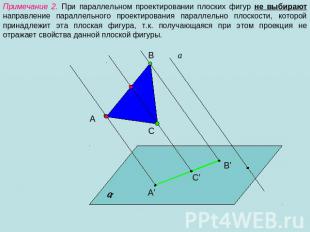
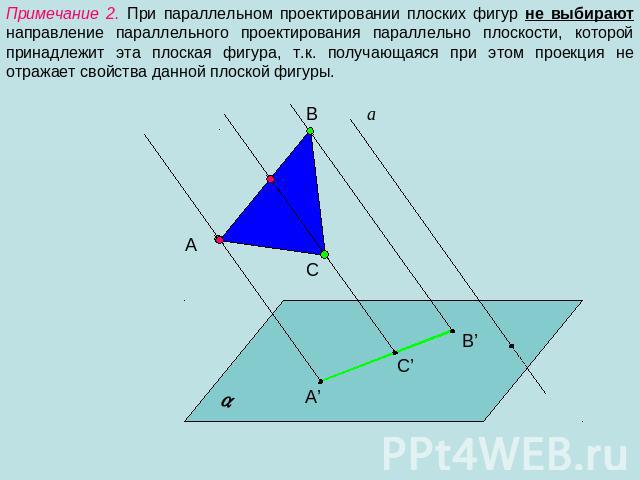
Примечание 2. При параллельном проектировании плоских фигур не выбирают направление параллельного проектирования параллельно плоскости, которой принадлежит эта плоская фигура, т.к. получающаяся при этом проекция не отражает свойства данной плоской фигуры.

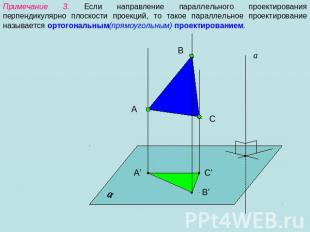
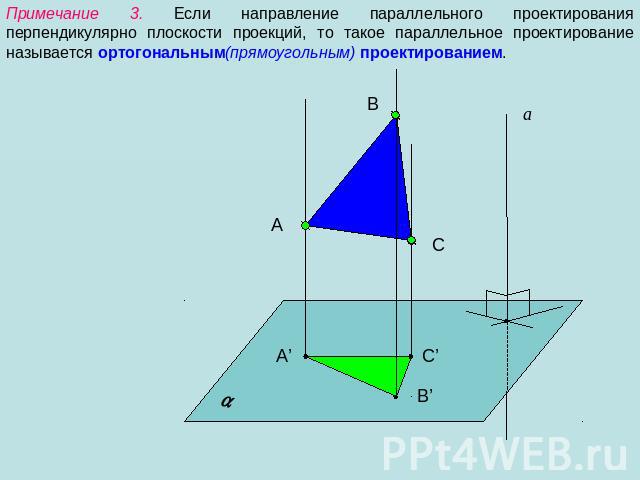
Примечание 3. Если направление параллельного проектирования перпендикулярно плоскости проекций, то такое параллельное проектирование называется ортогональным(прямоугольным) проектированием.

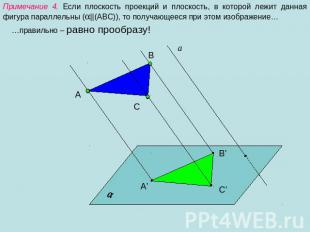
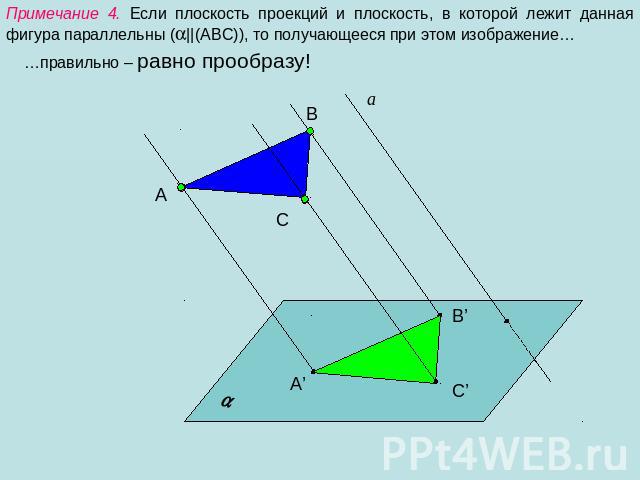
Примечание 4. Если плоскость проекций и плоскость, в которой лежит данная фигура параллельны (||(АВС)), то получающееся при этом изображение… …правильно – равно прообразу!

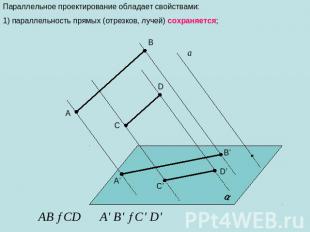
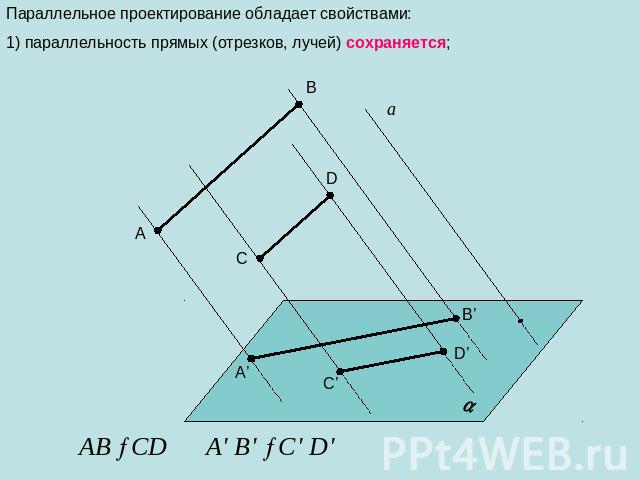
Параллельное проектирование обладает свойствами: 1) параллельность прямых (отрезков, лучей) сохраняется;

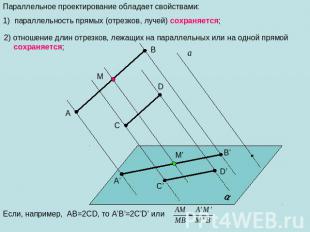
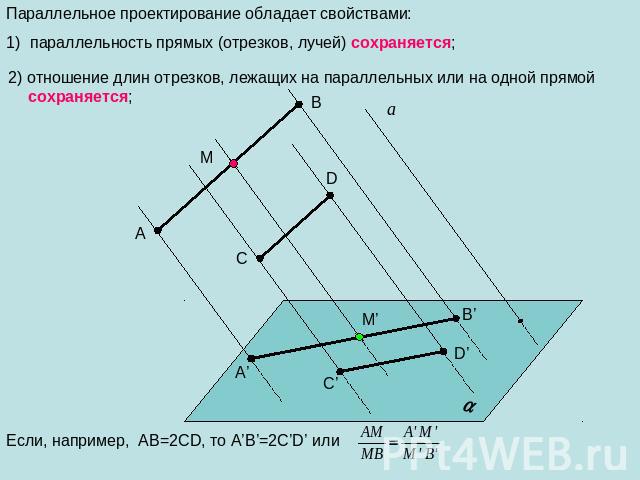
Параллельное проектирование обладает свойствами: параллельность прямых (отрезков, лучей) сохраняется; 2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется; Если, например, АВ=2CD, то А’В’=2C’D’ или

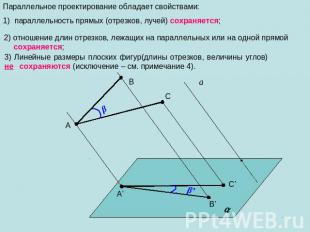
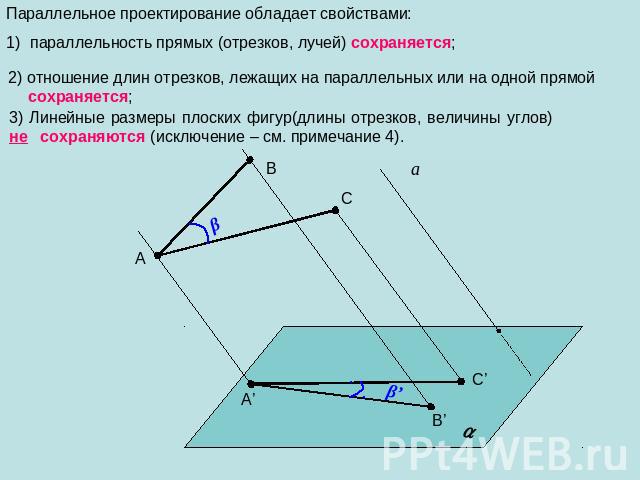
Параллельное проектирование обладает свойствами: параллельность прямых (отрезков, лучей) сохраняется; 2) отношение длин отрезков, лежащих на параллельных или на одной прямой сохраняется; 3) Линейные размеры плоских фигур(длины отрезков, величины углов) не сохраняются (исключение – см. примечание 4).

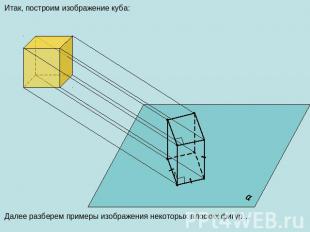
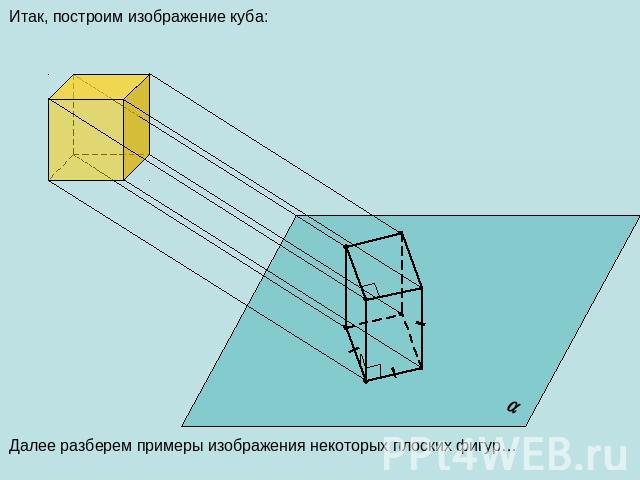
Итак, построим изображение куба: Далее разберем примеры изображения некоторых плоских фигур…

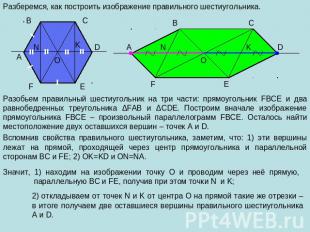
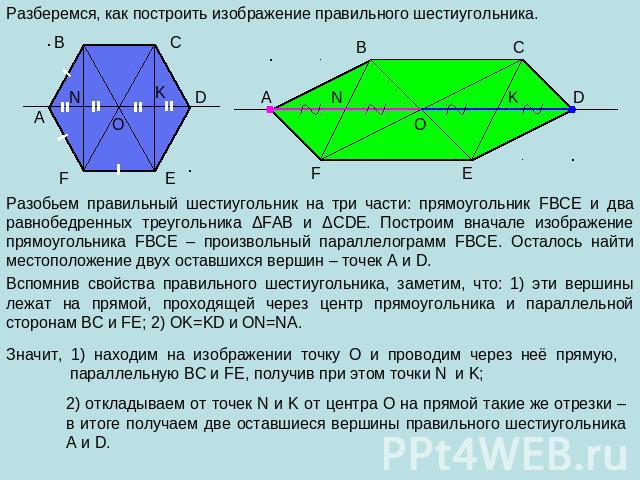
Разберемся, как построить изображение правильного шестиугольника. Разобьем правильный шестиугольник на три части: прямоугольник FBCE и два равнобедренных треугольника ΔFAB и ΔCDE. Построим вначале изображение прямоугольника FBCE – произвольный параллелограмм FBCE. Осталось найти местоположение двух оставшихся вершин – точек A и D. Вспомнив свойства правильного шестиугольника, заметим, что: 1) эти вершины лежат на прямой, проходящей через центр прямоугольника и параллельной сторонам BC и FE; 2) OK=KD и ON=NA. Значит, 1) находим на изображении точку О и проводим через неё прямую, параллельную BC и FE, получив при этом точки N и K; 2) откладываем от точек N и K от центра О на прямой такие же отрезки – в итоге получаем две оставшиеся вершины правильного шестиугольника A и D.

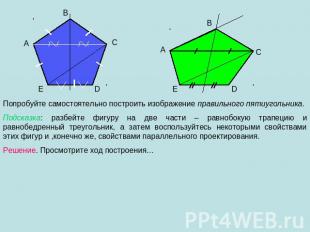
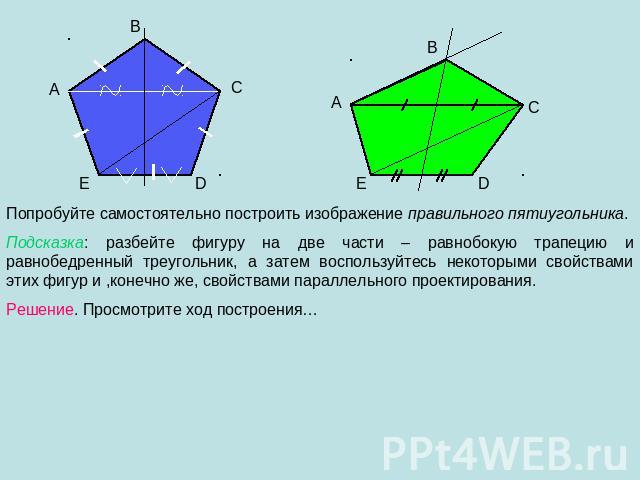
Попробуйте самостоятельно построить изображение правильного пятиугольника. Подсказка: разбейте фигуру на две части – равнобокую трапецию и равнобедренный треугольник, а затем воспользуйтесь некоторыми свойствами этих фигур и ,конечно же, свойствами параллельного проектирования. Решение. Просмотрите ход построения…