Презентация на тему: Треугольник и его свойства

Цели урока: Обобщить изученный материал по данной теме; Формировать умения применять математические знания к решению практических задач; Развивать познавательную активность, творческие способности; Воспитывать интерес к предмету.

Условия состязания Быть внимательным и сообразительным. Не оставлять ни одного вопроса без ответа. На каждое задание затрачивать минимум времени, но максимум усердия. Не подглядывать, не подслушивать, не «проникать» в мысли соседа.

Глядя на мир, нельзя не удивляться! К. Прутков

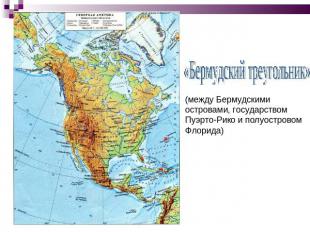
«Бермудский треугольник» (между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида)

Что такое треугольник? Назовите вершины и стороны треугольника, изображенного на рисунке Что такое треугольник? Назовите вершины и стороны треугольника, изображенного на рисунке

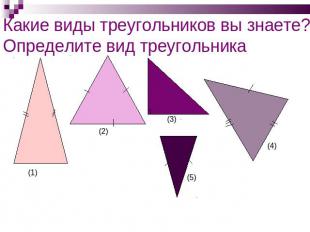
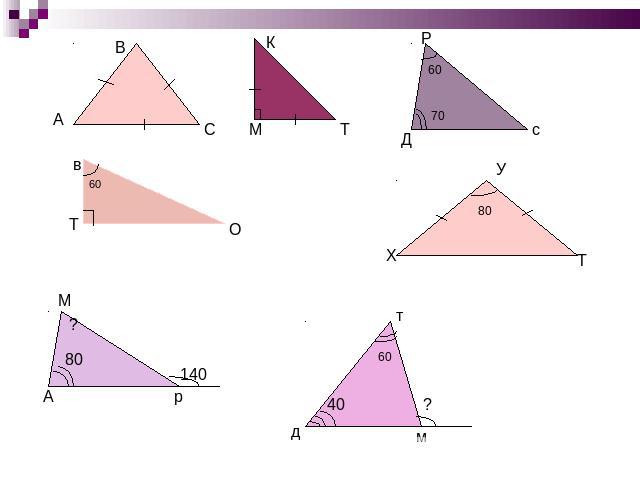
Какие виды треугольников вы знаете? Определите вид треугольника

Определите какие из следующих треугольников существуют Определите какие из следующих треугольников существуют 1гр. 7см, 7см, 7см; 4м, 8м, 4м. 2 гр. 12дм, 3дм, 8дм; 7м, 8м, 7м. 3 гр. 1дм, 14см, 22см; 3см,4см, 5дм. Назовите виды треугольников.

1гр. Найдите периметр треугольника, если известно, что его стороны равны 8см,9см,10см. 2гр. В равнобедренном треугольнике основание равно 6см, а боковая сторона больше основания на 2,5 см. Найдите периметр треугольника. 3гр. Периметр равнобедренного треугольника равен 21см. Известно, что его боковая сторона больше основания в 3 раза. Найдите стороны треугольника

Найдите все треугольники. Длины сторон которых – целые числа, не большие 2. Подсказка: Используйте неравенство треугольника.

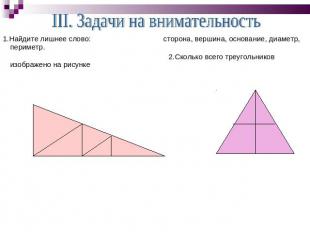
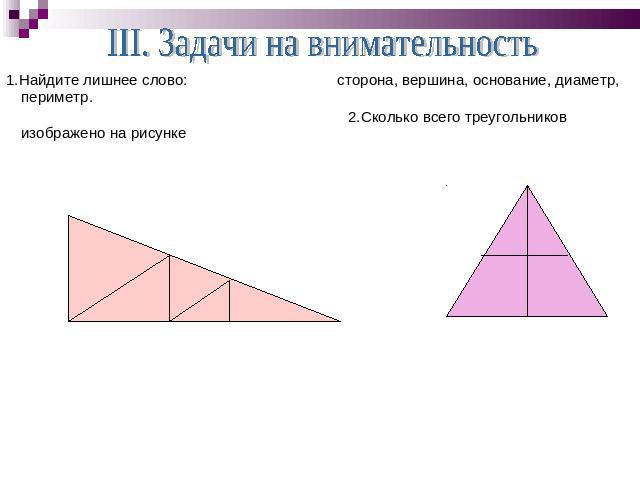
1.Найдите лишнее слово: сторона, вершина, основание, диаметр, периметр. 1.Найдите лишнее слово: сторона, вершина, основание, диаметр, периметр. 2.Сколько всего треугольников изображено на рисунке

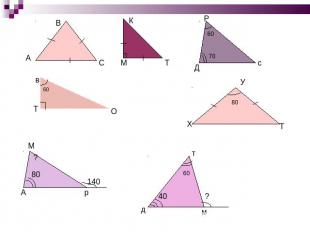
Углы треугольника Каким инструментом измеряют углы треугольника? Чему равна сумма углов в треугольнике? Что называют внешнем углом треугольника? Чему он равен?

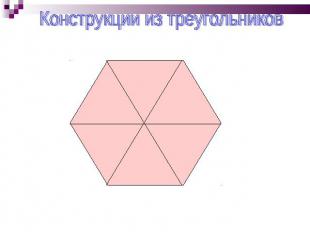
Конструкции из треугольников

Практическое применение

Крышу поддерживают наклонные балки – стропила

Геометрическая фигура«флексагон» (от англ. to flex,что означает «складываться, гнуться») Флексагон – «гнущийся» многоугольник, который состоит из10 равносторонних треугольников Флексагон обладает удивительной способностью внезапно менять свою форму и цвет, выворачиваясь на «изнанку».

Землемеры Древнего Египта для построения прямого угла пользовались следующим приемом. Бечевку делили узлами на 12 равных частей и концы связывали. Затем бечевку растягивали на земле так, чтобы получался треугольник со сторонами 3, 4, 5. Угол треугольника, противолежащий стороне с пятью делениями, был прямой. В связи с указанным способом построение прямого угла, треугольник со сторонами 3, 4, 5 иногда называют египетским Землемеры Древнего Египта для построения прямого угла пользовались следующим приемом. Бечевку делили узлами на 12 равных частей и концы связывали. Затем бечевку растягивали на земле так, чтобы получался треугольник со сторонами 3, 4, 5. Угол треугольника, противолежащий стороне с пятью делениями, был прямой. В связи с указанным способом построение прямого угла, треугольник со сторонами 3, 4, 5 иногда называют египетским

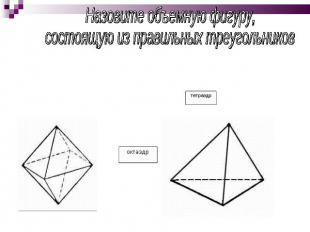
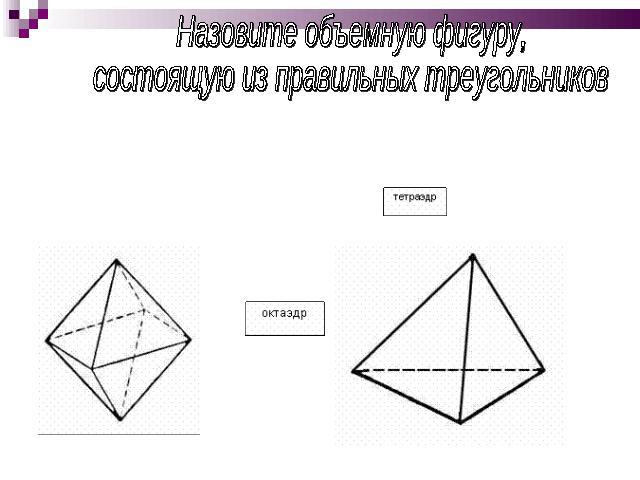
Назовите объемную фигуру, состоящую из правильных треугольников

Пирамида Хеопса Высота – 146,6 м, площадь основания -230×230(м²)

Тайна пирамиды Хеопса

Пирамиды «умеют» очень многое

Треугольник За один ход можно соединить две любые вершины шестиугольника. Каждый игрок следит, чтобы не получился треугольник, соединяющий три вершины шестиугольника, со сторонами такого же цвета, как его карандаш. На рисунке видно, что «Зеленый» проиграл.

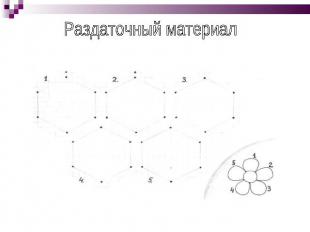
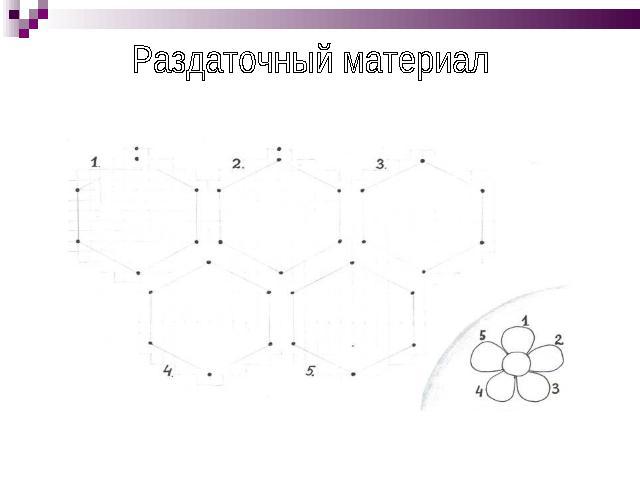
Раздаточный материал

Горки Начало игры в выделенной точке. Из этой точки начинают рисовать ломаную. За один ход обводят какую-нибудь сторону маленького треугольника. Ломаная может пересекать и касаться себя, но дважды обводить один отрезок нельзя! Кто будет вынужден нарушить это правило, проигрывает.

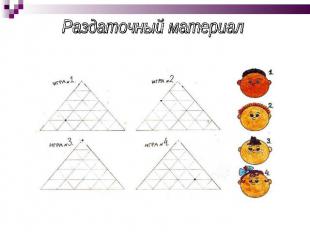
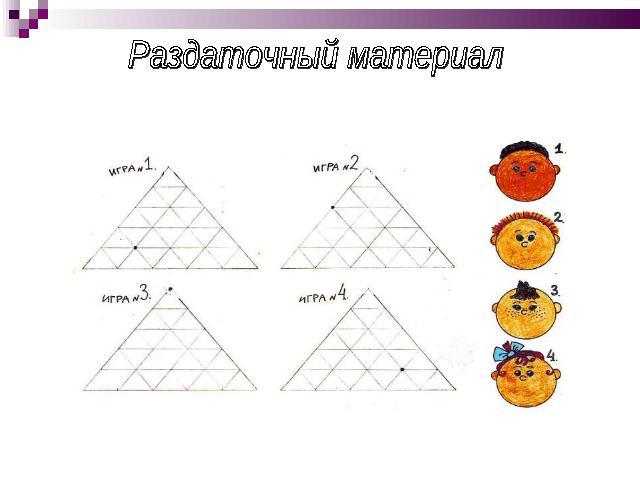
Раздаточный материал

« Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать» Галилео Галилей

Литература: 1. Геометрия 7-9. Л.С. Атанасян 2. За страницами учебника математики. И,Я.Депман, Н.Я.Виленкин. 3. Газета 1 сентября Математика №9, 14 2002 4. F:\математика\ Растрепанный Блокнот Флексагон.htm 5. Египетские Пирамиды фото http://www.estrintur.ru/tur/egypt/ http://www.147school.ru/photogallery?nom=8