Презентация на тему: Трехгранный угол

Урок 6 Трехгранный угол

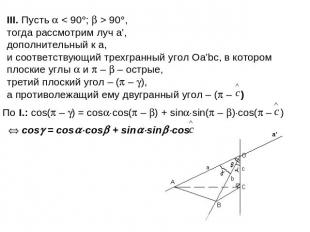
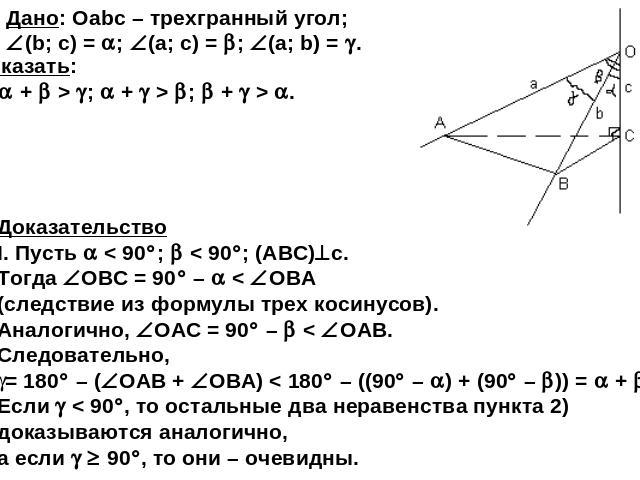
Основное свойство трехгранного угла. Теорема. В трехгранном угле сумма плоских углов меньше 360 и сумма любых двух из них больше третьего. Дано: Оabc – трехгранный угол;

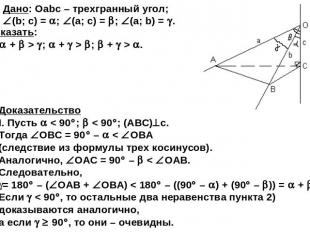
Дано: Оabc – трехгранный угол; (b; c) = ; (a; c) = ; (a; b) = . Доказать:

Формула трех косинусов Следствия. 1) Для вычисления угла между прямой и плоскостью применима формула: 2) Угол между прямой и плоскостью – наименьший из углов, которая эта прямая, образует с прямыми этой плоскости.

Дано: Оabc – трехгранный угол;

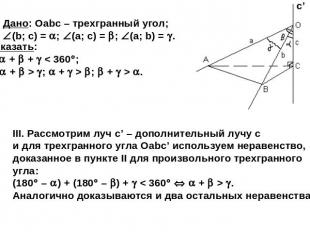
Следствие. В правильной треугольной пирамиде плоский угол при вершине меньше 120

Определение. Трехгранные углы называются равными если равны все их соответствующие плоские и двугранные углы. Признаки равенства трехгранных углов. Трехгранные углы равны, если у них соответственно равны: два плоских угла и двугранный угол между ними; 2) два двугранных угла и плоский угол между ними; 3) три плоских угла; 4) три двугранных угла.

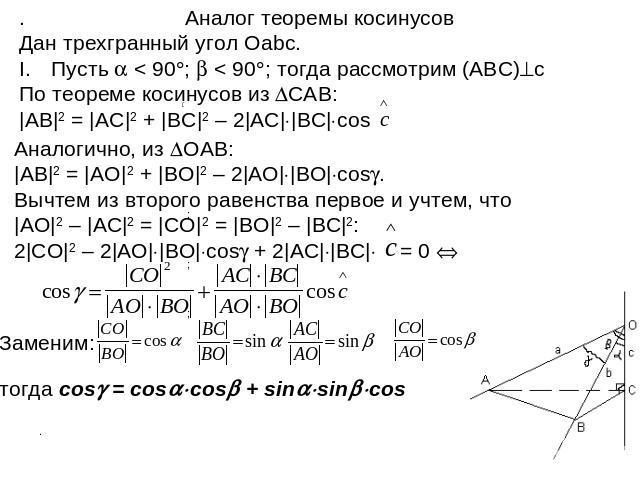
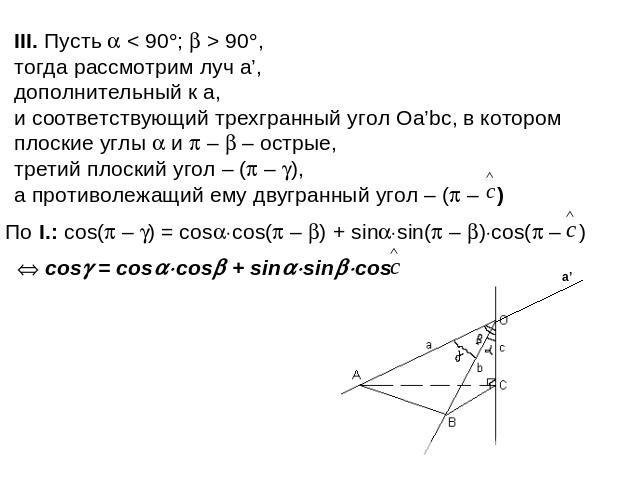
Аналог теоремы косинусов