Презентация на тему: Применение подобия треугольников к решению задач

Урок геометрии в 9 классе Автор: учитель математики МОУ СОШ № 74 г. Краснодара Забашта Елена Георгиевна

Применение подобия треугольников к решению задач

Цели урока: обучающая формировать умения и навыки применения теоретических знаний при решении задач; развивающая развивать сознательное восприятие учебного материала, прививать интерес к предмету; воспитывающая воспитывать познавательную активность, культуру общения.

Задачи урока: познакомить учащихся с принципом золотого сечения, показать его применение в искусстве, природе, архитектуре; рассмотреть применение подобия треугольников к решению практических задач.

Метод: исследование с применением теоретических знаний Оборудование: раздаточный материал ( цветной картон, ножницы), мультимедийный проектор, репродукции И.И. Шишкина «Сосновая роща», Леонардо да Винчи «Джоконда».

Ход урока. Природа Природа формулирует свои законы языком математики. Г. Галилей.

Немного о геометрии… Геометрия – это не просто наука о свойствах геометрических фигур. Геометрия – это целый мир, который окружает нас с самого рождения. Ведь все, что мы видим вокруг, так или иначе относится к геометрии, ничто не ускользает от ее внимательного взгляда. Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.

Компьютерная презентация о «золотом сечении» Принцип золотого сечения – высшее проявление структурного и функцио- нального совершенства целого и его частей в искусстве, науке, технике и природе. Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. Следуй девизу «смотри – думай – делай выводы»

Золотое сечение в картине Леонардо да Винчи «Джоконда» Портрет Моны Лизы привлекает тем, что композиция рисунка построена на «золотых треугольниках (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).

Золотое сечение в картине И.И. Шишкина «Сосновая роща» Наличие в картине ярких вертикалей и горизонталей, делящих ее в отношении золотого сечения, придает ей характер уравновешенности и спокойствия, в соответствии с замыслом художника.

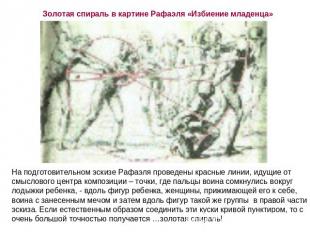
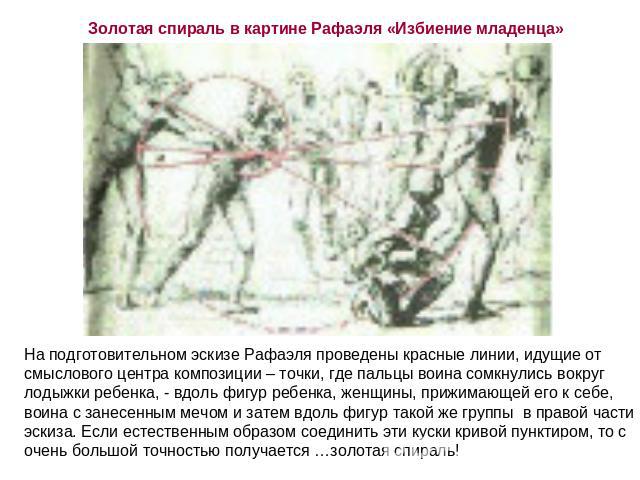
Золотая спираль в картине Рафаэля «Избиение младенца» На подготовительном эскизе Рафаэля проведены красные линии, идущие от смыслового центра композиции – точки, где пальцы воина сомкнулись вокруг лодыжки ребенка, - вдоль фигур ребенка, женщины, прижимающей его к себе, воина с занесенным мечом и затем вдоль фигур такой же группы в правой части эскиза. Если естественным образом соединить эти куски кривой пунктиром, то с очень большой точностью получается …золотая спираль!

Храм Парфенон в Афинах Даже сейчас, когда он стоит на развалинах, это одно из самых красивых сооружений мира. Этот храм построен в эпоху расцвета древнегреческой математики. И его красота основана на строгих математических законах. Если мы опишем около фасада Парфенона прямоугольник, то окажется, что его стороны образуют золотое сечение. Такой прямоугольник назвали «золотым прямоугольником»

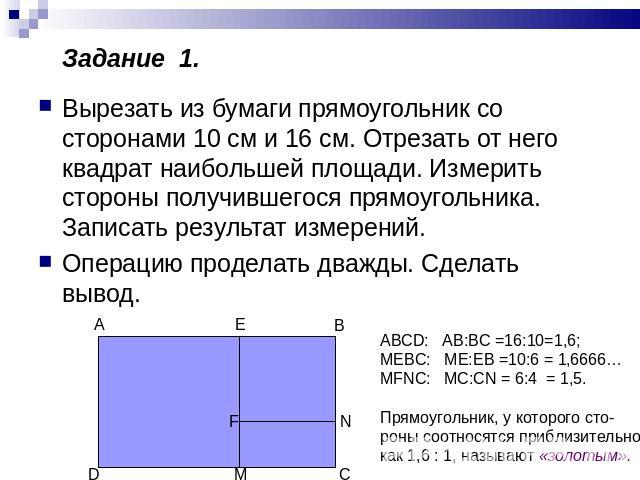
Задание 1. Вырезать из бумаги прямоугольник со сторонами 10 см и 16 см. Отрезать от него квадрат наибольшей площади. Измерить стороны получившегося прямоугольника. Записать результат измерений. Операцию проделать дважды. Сделать вывод. ABCD: AB:BC =16:10=1,6; MEBC: ME:EB =10:6 = 1,6666… MFNC: MC:CN = 6:4 = 1,5. Прямоугольник, у которого сто- роны соотносятся приблизительно как 1,6 : 1, называют «золотым».

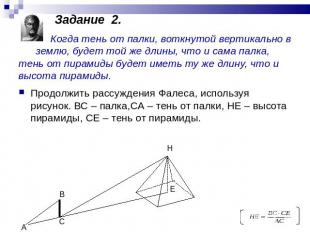
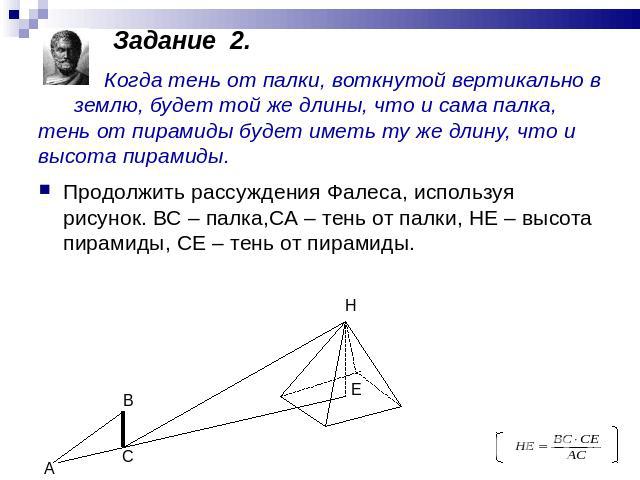
Задание 2. Когда тень от палки, воткнутой вертикально в землю, будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды. Продолжить рассуждения Фалеса, используя рисунок. ВС – палка,СА – тень от палки, НЕ – высота пирамиды, СЕ – тень от пирамиды.

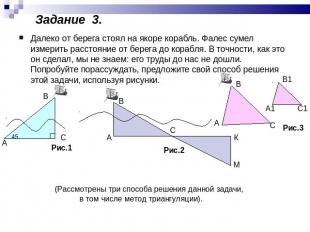
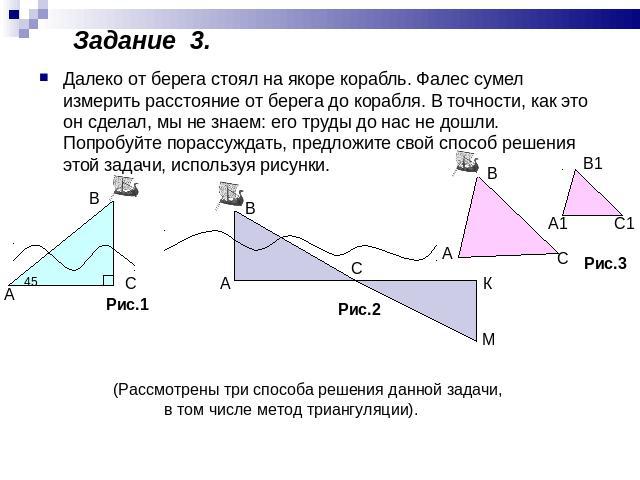
Далеко от берега стоял на якоре корабль. Фалес сумел измерить расстояние от берега до корабля. В точности, как это он сделал, мы не знаем: его труды до нас не дошли. Попробуйте порассуждать, предложите свой способ решения этой задачи, используя рисунки.

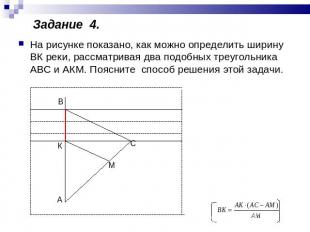
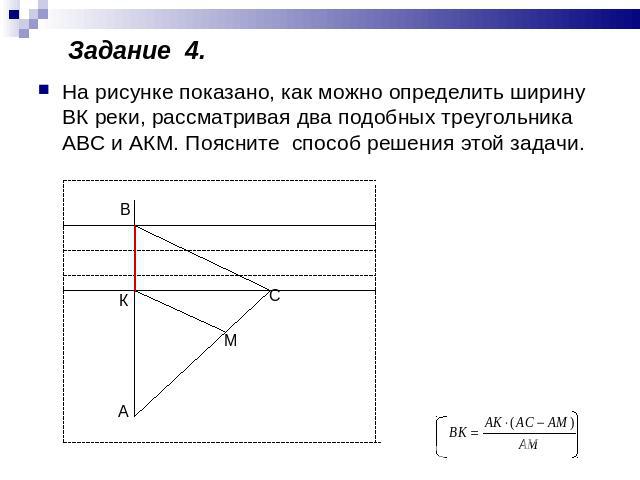
На рисунке показано, как можно определить ширину ВК реки, рассматривая два подобных треугольника АВС и АКМ. Поясните способ решения этой задачи.

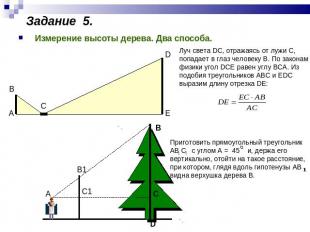
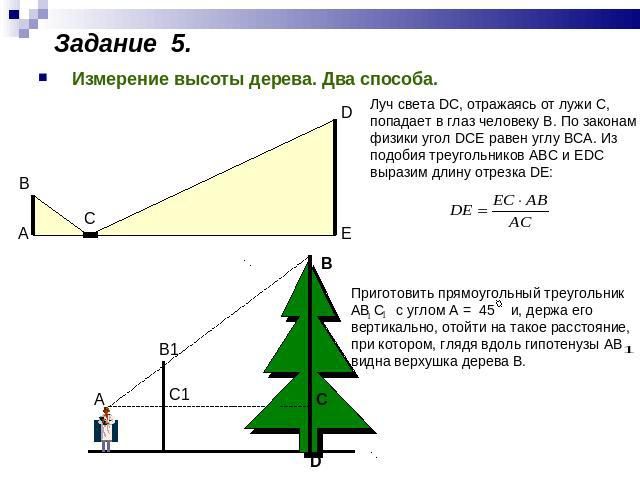
Задание 5. Измерение высоты дерева. Два способа. Луч света DC, отражаясь от лужи С, попадает в глаз человеку В. По законам физики угол DCE равен углу ВСА. Из подобия треугольников АВС и ЕDС выразим длину отрезка DЕ: Приготовить прямоугольный треугольник АВ С с углом А = 45 и, держа его вертикально, отойти на такое расстояние, при котором, глядя вдоль гипотенузы АВ , видна верхушка дерева В.

1. Определить ширину реки (задание 4), если АС = 100 м, АМ = 32 м, АК = 34 м. 2. Длина тени дерева равна 10,2 м, а длина тени человека, рост которого 1,7 м, равна 2,5 м. Найдите высоту дерева.

Итог урока. Не делай никогда того, чего не знаешь, но научись всему, что следует знать ПИФАГОР