Презентация на тему: Прямоугольный треугольник

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК Презентация разработана учителем математики МОУ «Корниловская средняя школа» Купцовой Е.В.

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК- ЭТО ТРЕУГОЛЬНИК, В КОТОРОМ ОДИН ИЗ УГЛОВ ПРЯМОЙ (90)
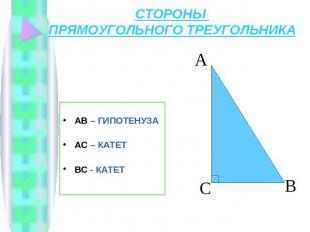
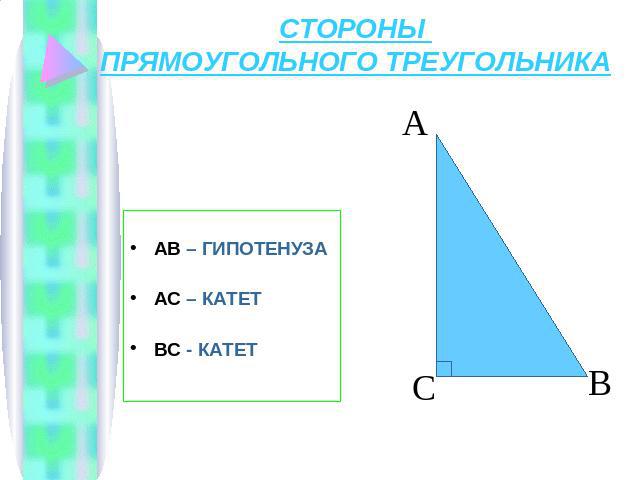
СТОРОНЫ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКААВ – ГИПОТЕНУЗА АС – КАТЕТ ВС - КАТЕТ

ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
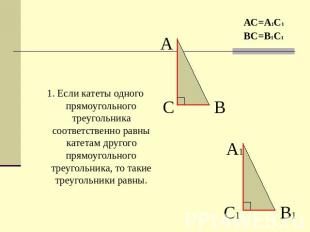
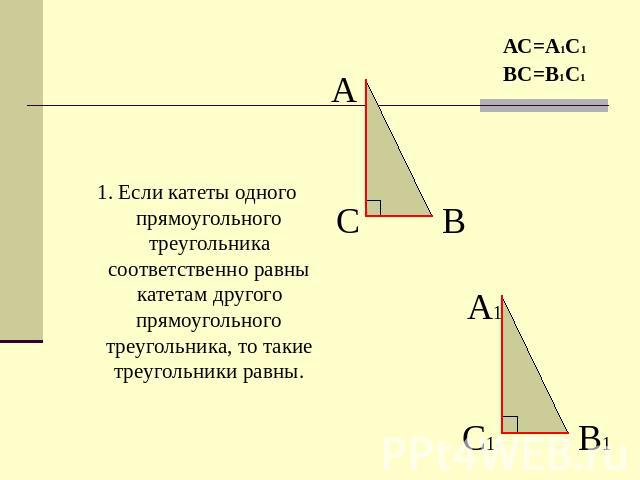
1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
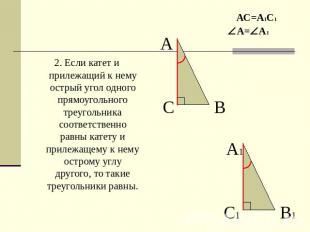
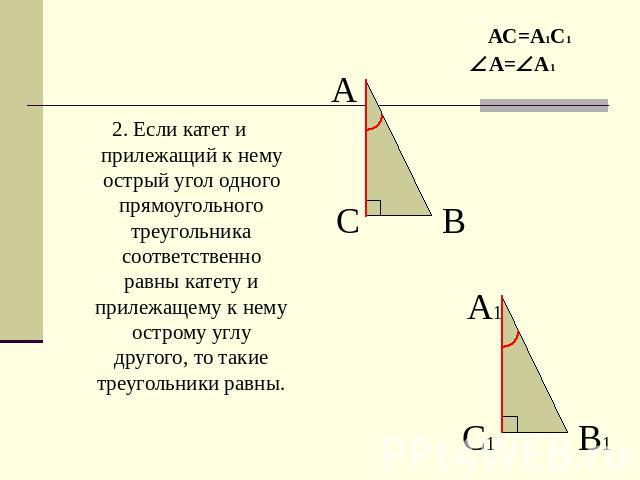
2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
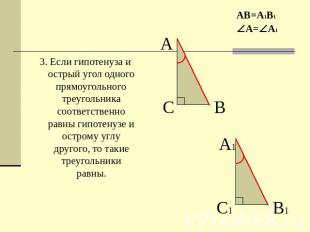
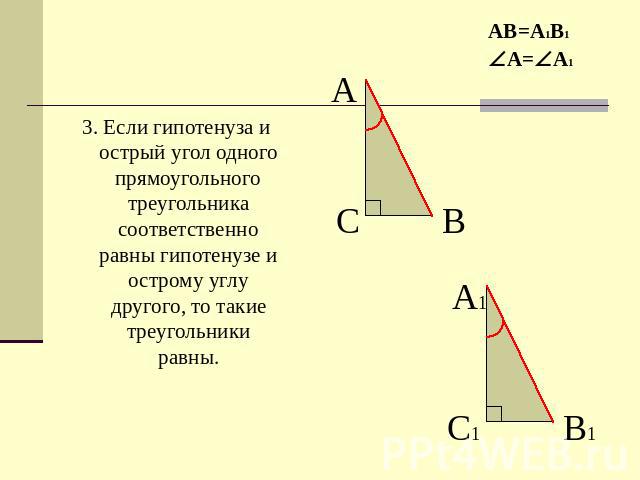
3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
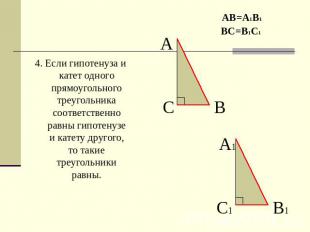
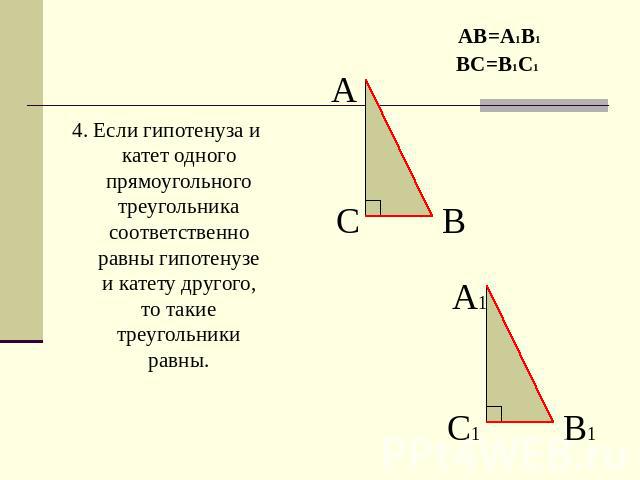
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

НЕКОТОРЫЕ СВОЙСТВА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА
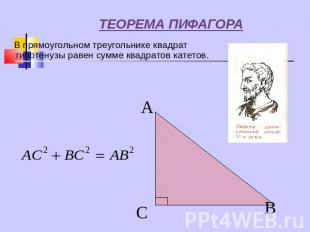
ТЕОРЕМА ПИФАГОРА В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Сумма острых углов прямоугольного треугольника равна 90
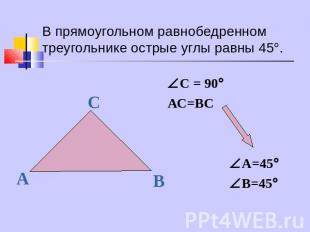
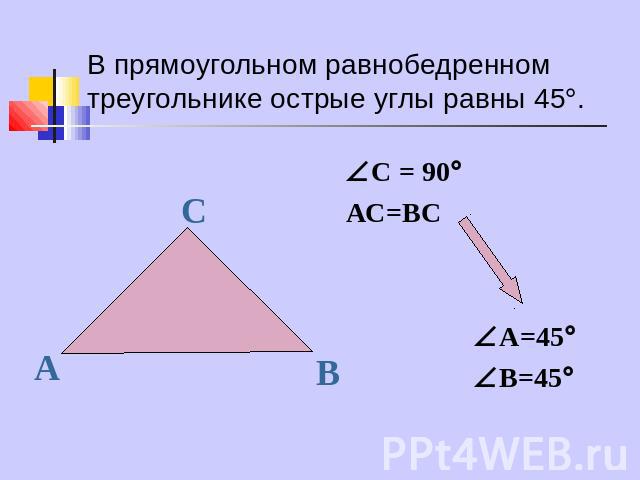
В прямоугольном равнобедренном треугольнике острые углы равны 45.
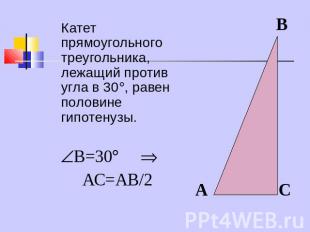
Катет прямоугольного треугольника, лежащий против угла в 30, равен половине гипотенузы.
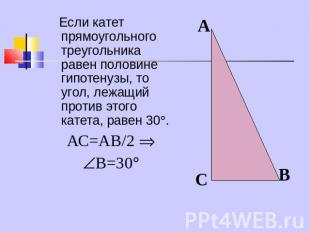
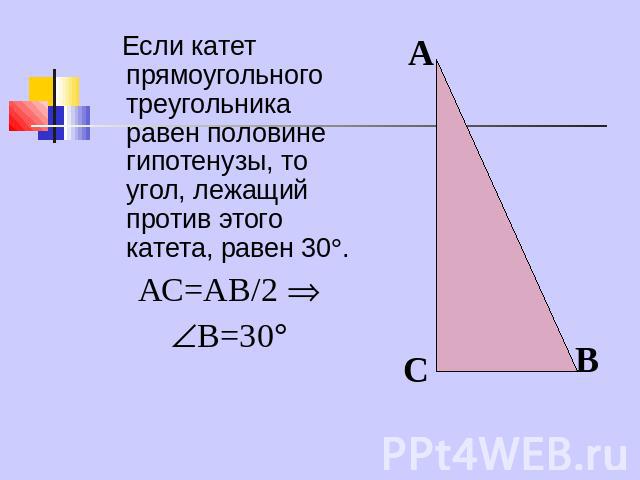
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30. АС=АВ/2 В=30
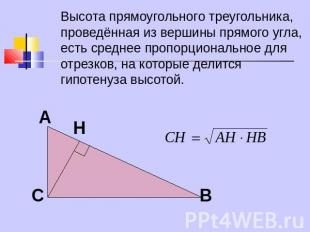
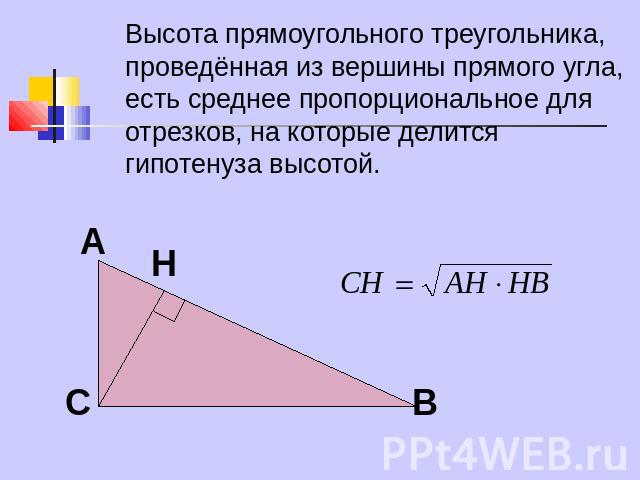
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза высотой.
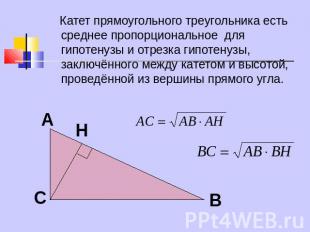
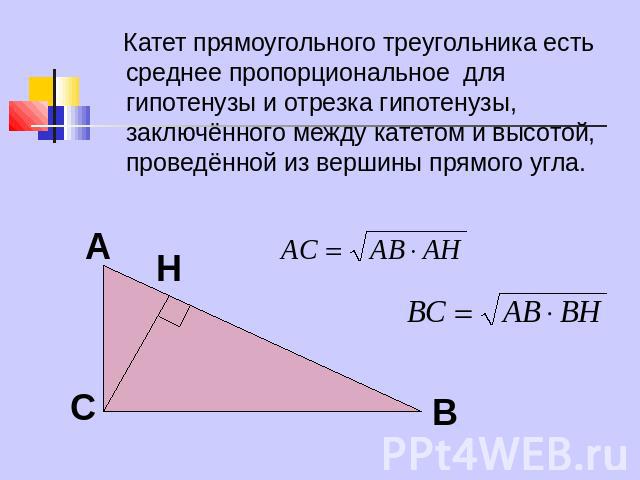
Катет прямоугольного треугольника есть среднее пропорциональное для гипотенузы и отрезка гипотенузы, заключённого между катетом и высотой, проведённой из вершины прямого угла.