Презентация на тему: Тригонометрические уравнения и неравенства

Тригонометрические уравнения и неравенства

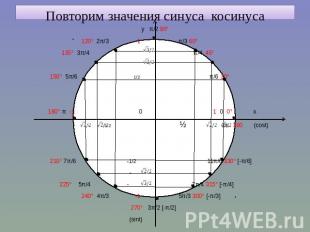
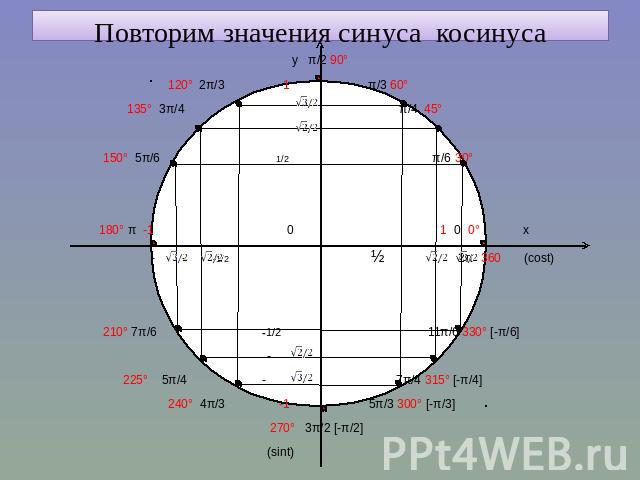
Повторим значения синуса косинуса

Арксинус Арксинусом числа а называется такое число (угол) t из [-π/2;π/2], что sin t = а. Причём, | а |≤ 1.

Арккосинус Арккосинусом числа а называется такое число (угол) t из [0;π], что cos t = а. Причём, | а |≤ 1.

При каких значениях х имеет смысл выражение:

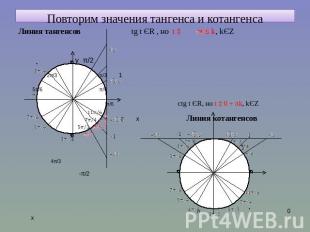
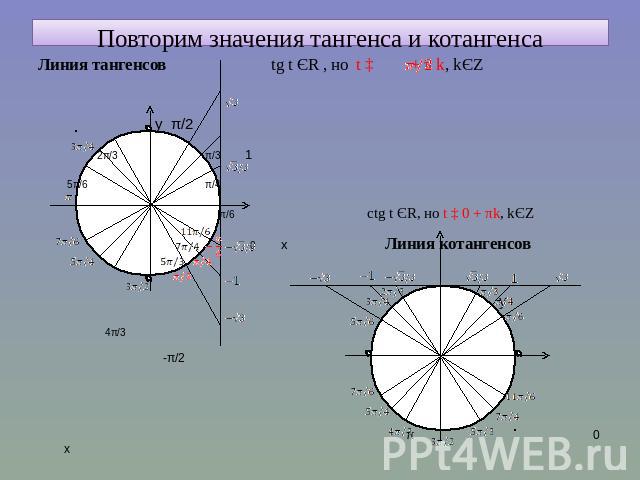
Повторим значения тангенса и котангенса Линия тангенсов

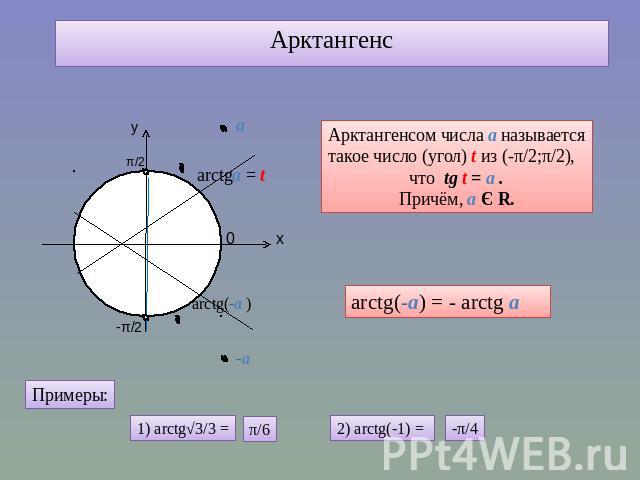
Арктангенс Арктангенсом числа а называется такое число (угол) t из (-π/2;π/2), что tg t = а . Причём, а Є R.

Арккотангенс Арккотангенсом числа а называется такое число (угол) t из (0;π), что ctg t = а. Причём, а ЄR .

Формулы корней простых тригонометрических уравнений

Примеры

Решение простейших уравнений tg2x = -1 2x = arctg (-1) + πk, kЄZ 2x = -π/4 + πk, kЄZ x = -π/8 + πk/2, kЄZ Ответ: -π/8 + πk/2, kЄZ. ) cos(x+π/3) = ½ x+π/3 = ±arccos1/2 + 2πk, kЄZ x+π/3 = ±π/3 + 2πk, kЄZ x = -π/3 ± π/3 + 2πk, kЄZ Ответ: -π/3 ± π/3 + 2πk, kЄZ sin(π – x/3) = 0 упростим по формулам приведения sin(x/3) = 0 частный случай x/3 = πk, kЄZ x = 3πk, kЄZ. Ответ: 3πk, kЄZ.

Другие тригонометрические уравнения 1.Сводимые к квадратным a∙sin²x + b∙sinx + c=0 Пусть sinx = p, где |p| ≤1, тогда a∙p² + b∙p + c = 0 Найти корни, вернуться к замене и решить простые уравнения. 2.Однородные 1)Первой степени: a∙sinx + b∙cosx = 0 Т.к. sinx и cosx одновременно не равны нулю, то разделим обе части уравнения на cosx. Получим: простое уравнение a∙tgx + b = 0 или tgx = m 2)Второй степени: a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0 Разделим обе части на cos²x. Получим квадратное уравнение: a∙tg²x + b∙tgx + c = 0.

Простые тригонометрические неравенства