Презентация на тему: Трёхгранный угол

Урок 6 Трехгранный угол 900igr.net

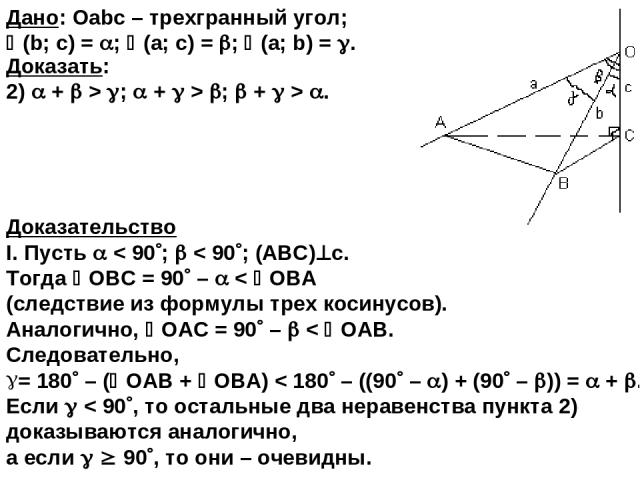
Теорема. В трехгранном угле сумма плоских углов меньше 360 и сумма любых двух из них больше третьего. Дано: Оabc – трехгранный угол; (b; c) = ; (a; c) = ; (a; b) = . Основное свойство трехгранного угла. Доказать: + + < 360 ; 2) + > ; + > ; + > .

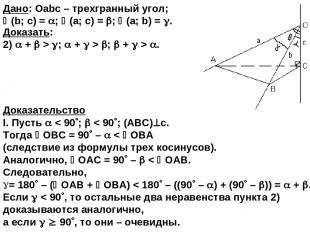
Доказательство I. Пусть < 90 ; < 90 ; (ABC) с. Тогда ОВС = 90 – < ОВА (следствие из формулы трех косинусов). Аналогично, ОАС = 90 – < ОAВ. Следовательно, = 180 – ( ОАB + ОBA) < 180 – ((90 – ) + (90 – )) = + . Если < 90 , то остальные два неравенства пункта 2) доказываются аналогично, а если 90 , то они – очевидны. Дано: Оabc – трехгранный угол; (b; c) = ; (a; c) = ; (a; b) = . Доказать: 2) + > ; + > ; + > .

Формула трех косинусов . Следствия. 1) Для вычисления угла между прямой и плоскостью применима формула: 2) Угол между прямой и плоскостью – наименьший из углов, которая эта прямая, образует с прямыми этой плоскости.

II. На ребрах данного угла отложим точки A’, B’ и C’ так, что |OA’| = |OB’| = |OC’| Тогда треугольники A’OB’, B’OC’ и С’OA’ – равнобедренные, а их углы при основаниях 1 – 6 – острые. Для трехгранных углов с вершинами A’, B’ и C’ применим неравенства, доказанные в пункте I: С’А’B’ < 1 + 6; А’B’C’ < 2 + 3; B’С’А’ < 4 + 5. Сложим эти неравенства почленно, тогда 180 < ( 1 + 2) + ( 3 + 4) + ( 5 + 6) = = (180 – ) + (180 – ) + (180 – ) + + < 360 . Дано: Оabc – трехгранный угол; (b; c) = ; (a; c) = ; (a; b) = . Доказать: + + < 360 ; 2) + > ; + > ; + > .

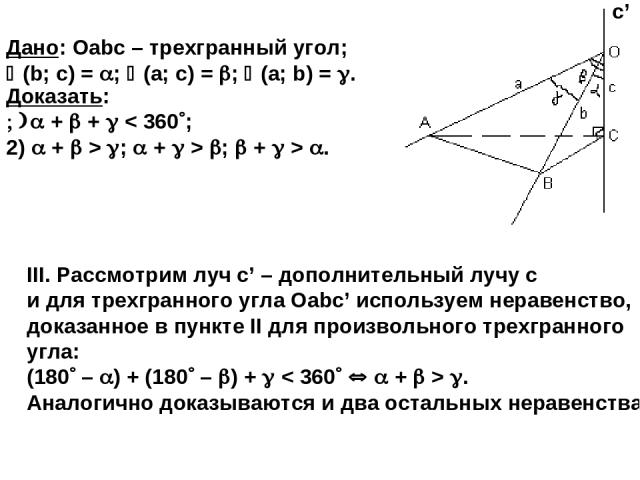
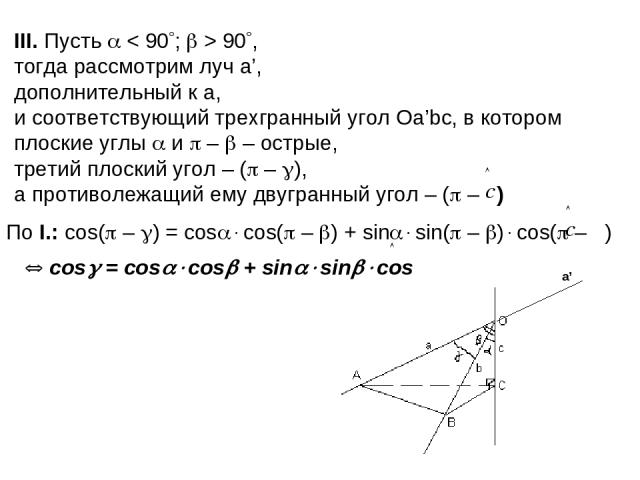
III. Рассмотрим луч c’ – дополнительный лучу с и для трехгранного угла Оabc’ используем неравенство, доказанное в пункте II для произвольного трехгранного угла: (180 – ) + (180 – ) + < 360 + > . Аналогично доказываются и два остальных неравенства. Дано: Оabc – трехгранный угол; (b; c) = ; (a; c) = ; (a; b) = . Доказать: + + < 360 ; 2) + > ; + > ; + > . с’

Следствие. В правильной треугольной пирамиде плоский угол при вершине меньше 120 .

Определение. Трехгранные углы называются равными если равны все их соответствующие плоские и двугранные углы. Признаки равенства трехгранных углов. Трехгранные углы равны, если у них соответственно равны: два плоских угла и двугранный угол между ними; 2) два двугранных угла и плоский угол между ними; 3) три плоских угла; 4) три двугранных угла. Рис. 4б

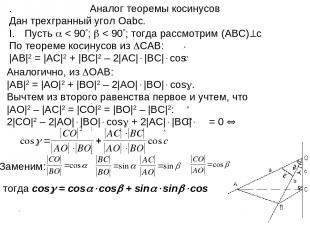
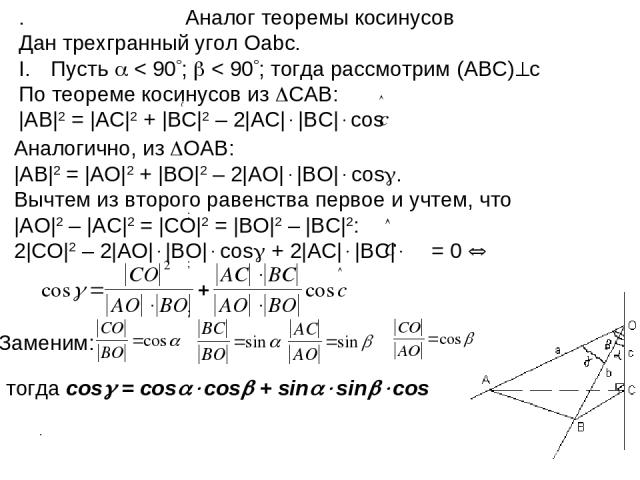
. . Дан трехгранный угол Оabc. Пусть < 90 ; < 90 ; тогда рассмотрим (ABC) с По теореме косинусов из CАВ: |AB|2 = |AC|2 + |BC|2 – 2|AC| |BC| cos Аналог теоремы косинусов Аналогично, из OАВ: |AB|2 = |AO|2 + |BO|2 – 2|AO| |BO| cos . Вычтем из второго равенства первое и учтем, что |AO|2 – |AC|2 = |CO|2 = |BO|2 – |BC|2: 2|CO|2 – 2|AO| |BO| cos + 2|AC| |BC| = 0 . ; ; ; тогда cos = cos cos + sin sin cos Заменим:

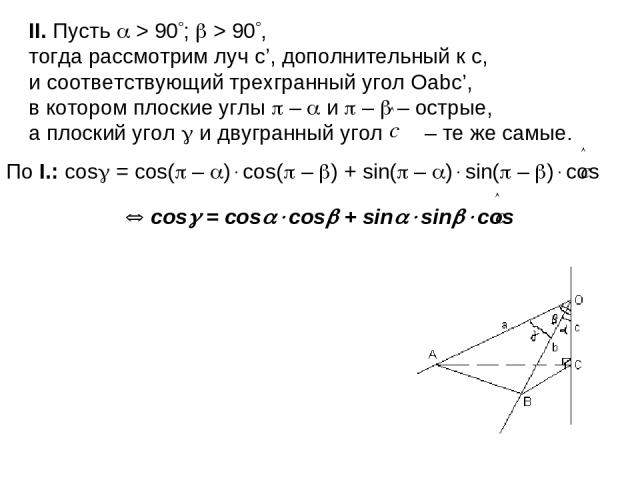
II. Пусть > 90 ; > 90 , тогда рассмотрим луч с’, дополнительный к с, и соответствующий трехгранный угол Оаbс’, в котором плоские углы – и – – острые, а плоский угол и двугранный угол – те же самые. По I.: cos = cos( – ) cos( – ) + sin( – ) sin( – ) cos cos = cos cos + sin sin cos

III. Пусть < 90 ; > 90 , тогда рассмотрим луч a’, дополнительный к a, и соответствующий трехгранный угол Оа’bс, в котором плоские углы и – – острые, третий плоский угол – ( – ), а противолежащий ему двугранный угол – ( – ) По I.: cos( – ) = cos cos( – ) + sin sin( – ) cos( – ) cos = cos cos + sin sin cos a’

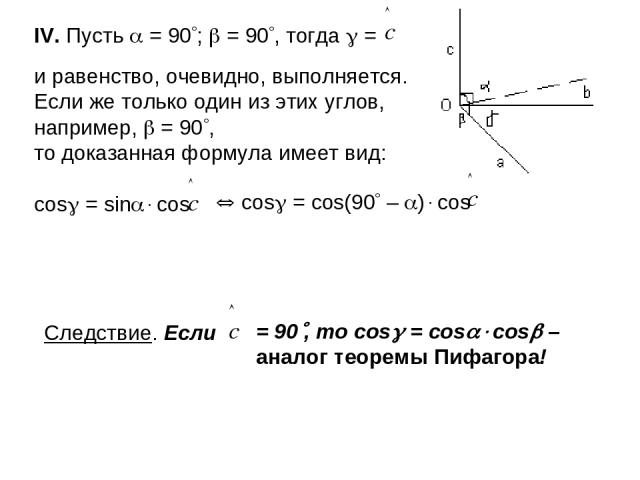
IV. Пусть = 90 ; = 90 , тогда = и равенство, очевидно, выполняется. Если же только один из этих углов, например, = 90 , то доказанная формула имеет вид: cos = sin cos cos = cos(90 – ) cos Следствие. Если = 90 , то cos = cos cos – аналог теоремы Пифагора!