Презентация на тему: Угол, вписанный в окружность

Угол, вписанный в окружность Работу выполнил ученик 9а класса МОУ СОШ п. Пяльма Плешков Александр

Центральным уголом в окружности называется плоский угол с вершиной в её центре

Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным в окружность

Теорема 11.5. Угол, вписанный в окружность, равен половине соответствующего центрального угла. Док-во. Рассмотрим сначала частный случай, когда одна из сторон угла проходит через центр окружности. Треугольник АОВ равнобедренный, так как у него стороны OA и ОВ равны как радиусы. Поэтому углы А и В треугольника равны. А так как их сумма равна внешнему углу треугольника при вершине О, то угол В треугольника равен половине угла АОС, что и требовалось доказать

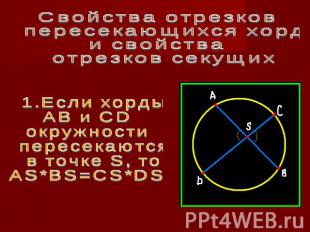
Свойства отрезков пересекающихся хорд и свойства отрезков секущих 1.Если хорды АВ и СD окружности пересекаются в точке S, то AS*BS=CS*DS

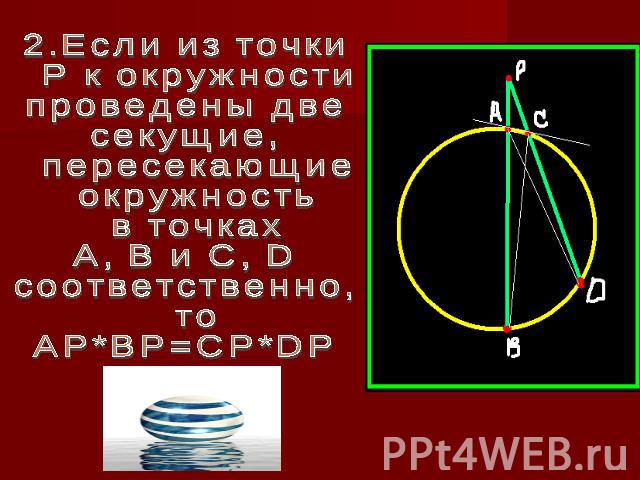
2.Если из точки P к окружности проведены две секущие, пересекающие окружность в точках А, В и С, D соответственно, то AP*BP=CP*DP