Презентация на тему: Окружность вписанная в многоугольник

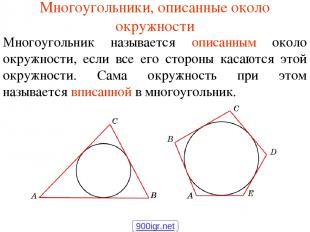
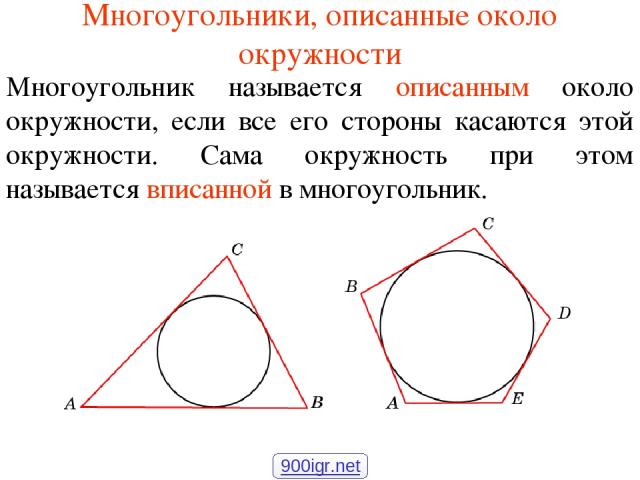
Многоугольники, описанные около окружности Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности. Сама окружность при этом называется вписанной в многоугольник. 900igr.net

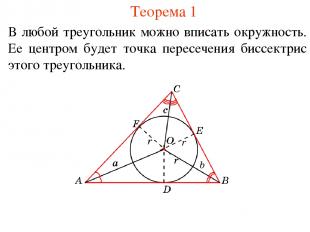
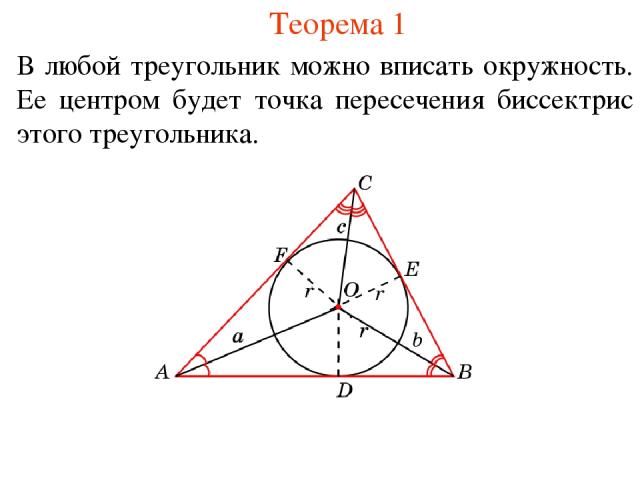
Теорема 1 В любой треугольник можно вписать окружность. Ее центром будет точка пересечения биссектрис этого треугольника.

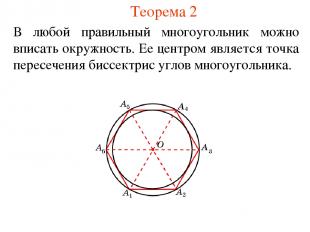
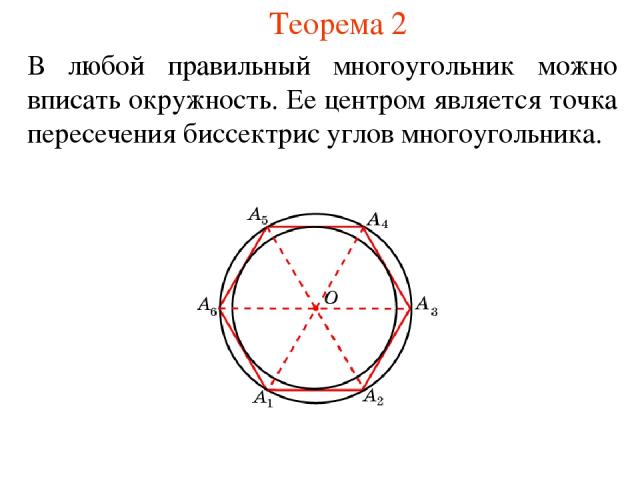
Теорема 2 В любой правильный многоугольник можно вписать окружность. Ее центром является точка пересечения биссектрис углов многоугольника.

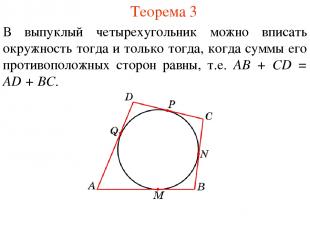
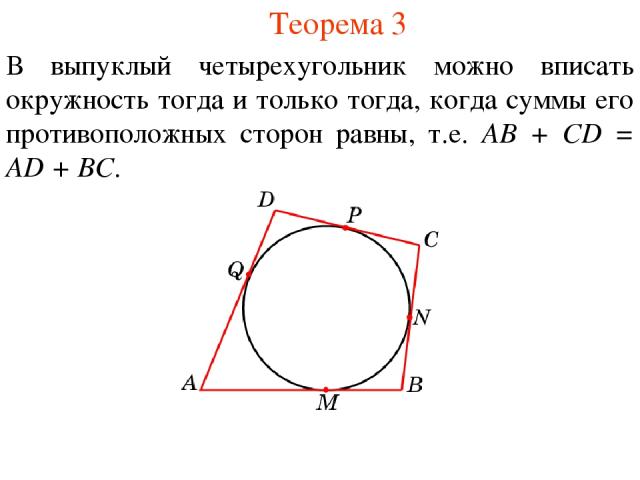
Теорема 3 В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны, т.е. AB + CD = AD + BC.

Вопрос 1 Какой многоугольник называется описанным около окружности? Ответ: Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности.

Вопрос 2 Какая окружность называется вписанной в многоугольник? Ответ: Вписанной в многоугольник называется окружность, касающаяся всех сторон этого многоугольника.

Вопрос 3 Во всякий ли треугольник можно вписать окружность? Ответ: Да.

Вопрос 4 Какая точка является центром вписанной в треугольник окружности? Ответ: Центром вписанной окружности является точка пересечения биссектрис этого треугольника.

Вопрос 5 В любой ли правильный многоугольник можно ли вписать окружность? Ответ: Да.

Вопрос 6 Можно ли вписать окружность в: а) остроугольный треугольник; б) прямоугольный треугольник; в) тупоугольный треугольник? Ответ: а) Да; б) да; в) да.

Вопрос 7 Может ли центр вписанной в треугольник окружности находиться вне этого треугольника? Ответ: Нет.

Вопрос 8 Какой вид имеет треугольник, если: а) центры вписанной и описанной около треугольника окружностей совпадают; б) центр вписанной в него окружности принадлежит одной из его высот? Ответ: а) Равносторонний; б) равнобедренный.

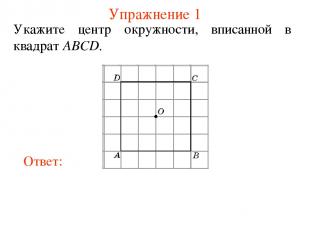
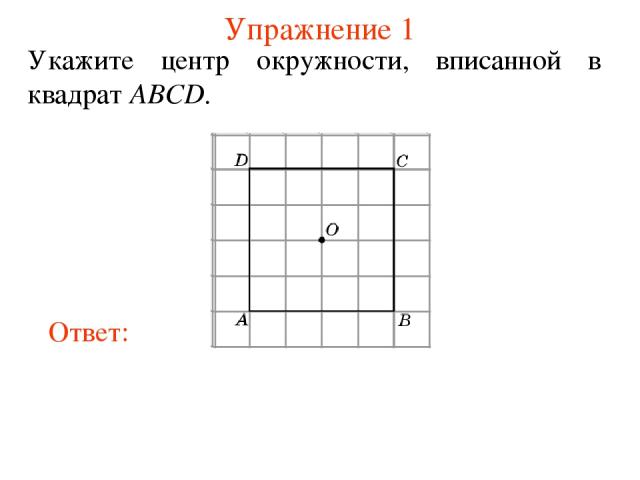
Упражнение 1 Укажите центр окружности, вписанной в квадрат ABCD.

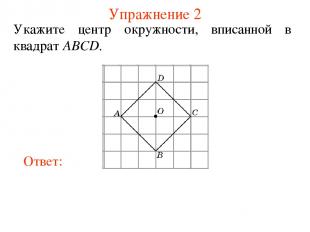
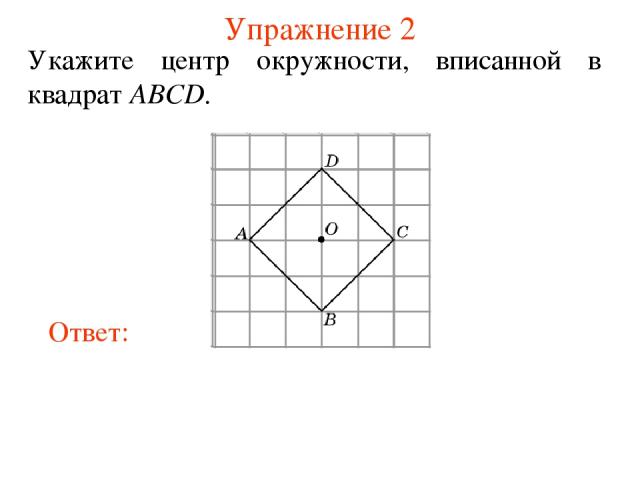
Упражнение 2 Укажите центр окружности, вписанной в квадрат ABCD.

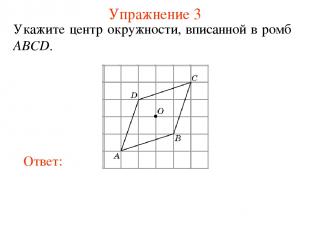
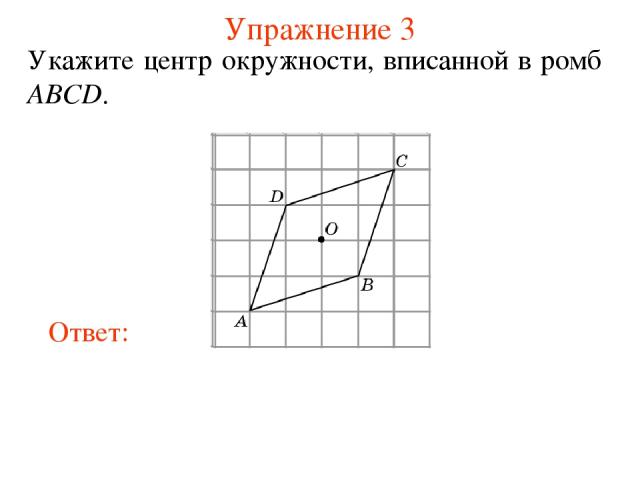
Упражнение 3 Укажите центр окружности, вписанной в ромб ABCD.

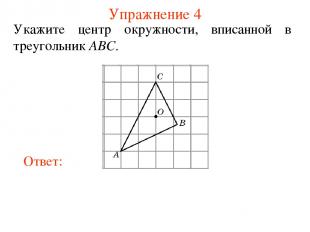
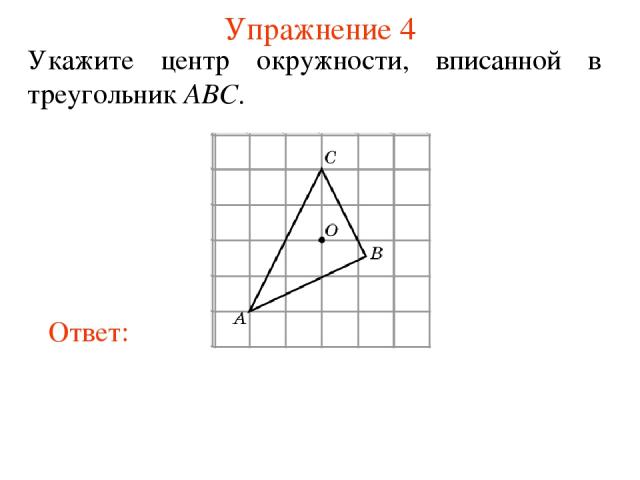
Упражнение 4 Укажите центр окружности, вписанной в треугольник ABC.

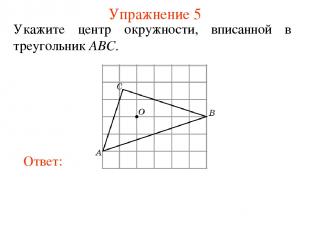
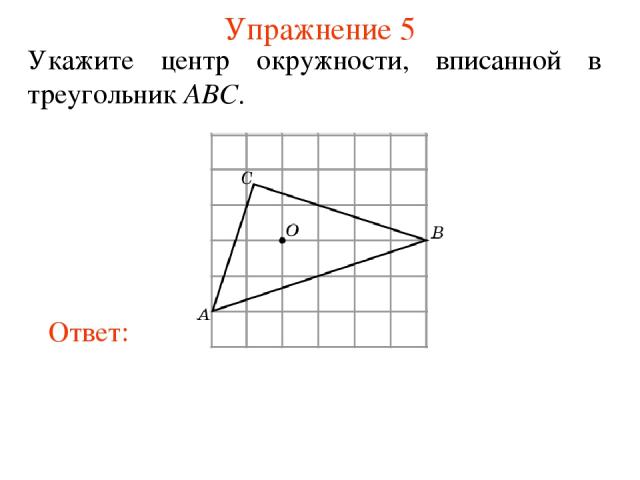
Упражнение 5 Укажите центр окружности, вписанной в треугольник ABC.

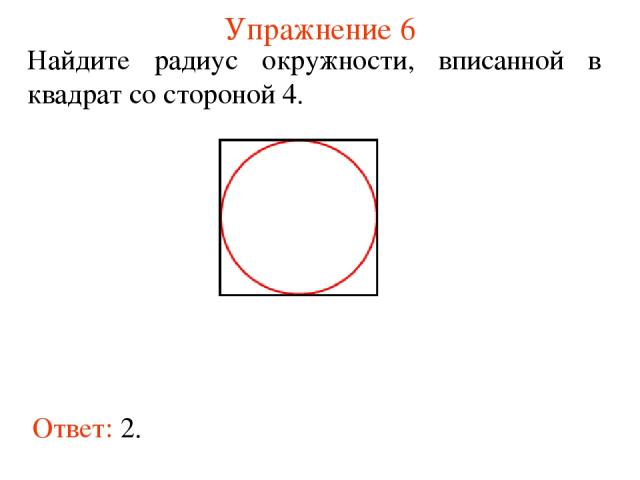
Упражнение 6 Ответ: 2. Найдите радиус окружности, вписанной в квадрат со стороной 4.

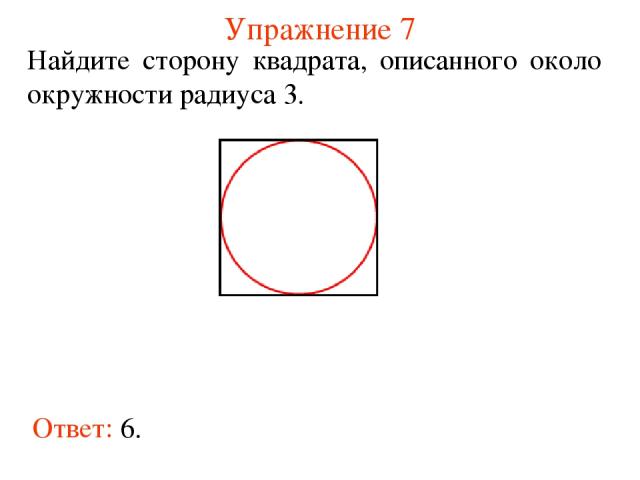
Упражнение 7 Ответ: 6. Найдите сторону квадрата, описанного около окружности радиуса 3.

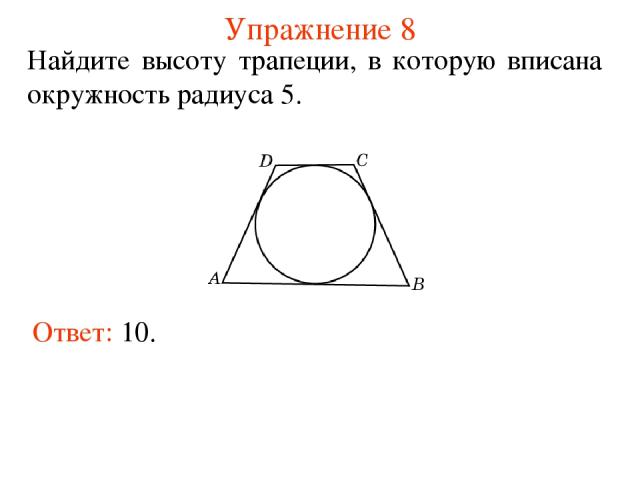
Упражнение 8 Ответ: 10. Найдите высоту трапеции, в которую вписана окружность радиуса 5.

Упражнение 9 Окружность, вписанная в треугольник ABC, делит сторону AB в точке касания D на два отрезка AD = 5 см и DB = 6 см. Найдите периметр треугольника ABC, если известно, что BC = 10 см. Ответ: 30 см.

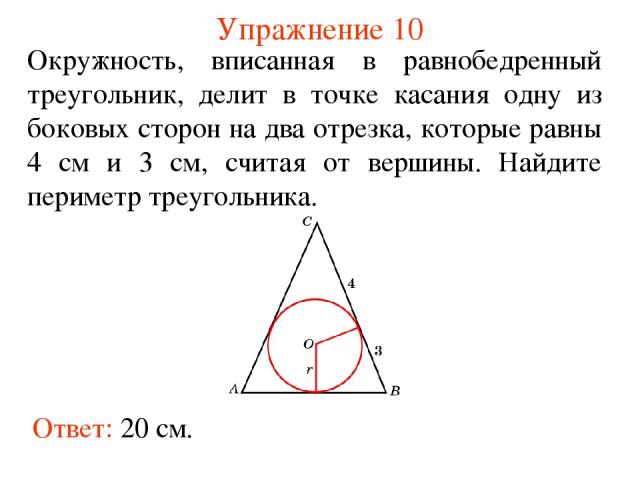
Упражнение 10 Ответ: 20 см. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, которые равны 4 см и 3 см, считая от вершины. Найдите периметр треугольника.

Упражнение 11 К окружности, вписанной в треугольник АВС, проведены три касательные. Периметры отсеченных треугольников равны p1, p2, p3. Найдите периметр данного треугольника. Ответ: p1 + p2 + p3.

Упражнение 12 Ответ: 34 см. В равнобедренном треугольнике боковые стороны делятся точками касания вписанной в треугольник окружности в отношении 7:5, считая от вершины, противоположной основанию. Найдите периметр треугольника, если его основание равно 10 см.

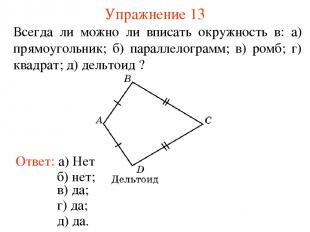
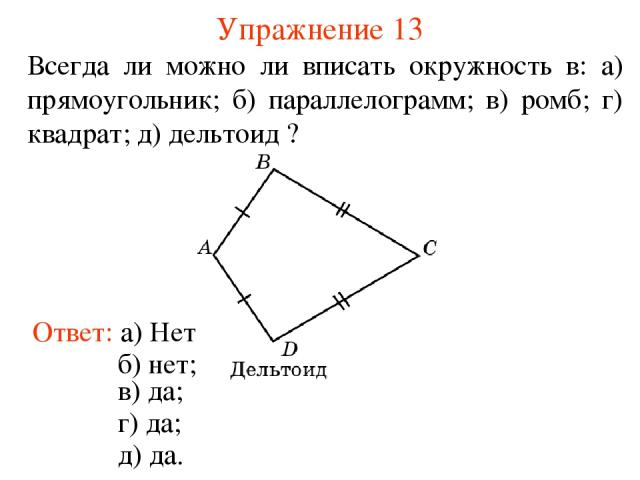
Упражнение 13 Ответ: а) Нет; Всегда ли можно ли вписать окружность в: а) прямоугольник; б) параллелограмм; в) ромб; г) квадрат; д) дельтоид ? б) нет; в) да; г) да; д) да.

Упражнение 14 Два равнобедренных треугольника имеют общее основание и расположены по разные стороны от него. Можно ли в образованный ими выпуклый четырехугольник вписать окружность? Ответ: Да.

Упражнение 15 Какой вид имеет четырехугольник, если центр вписанной в него окружности совпадает с точкой пересечения диагоналей? Ответ: Ромб.

Упражнение 16 Около окружности описана трапеция, периметр которой равен 18 см. Найдите ее среднюю линию. Ответ: 4,5 см.

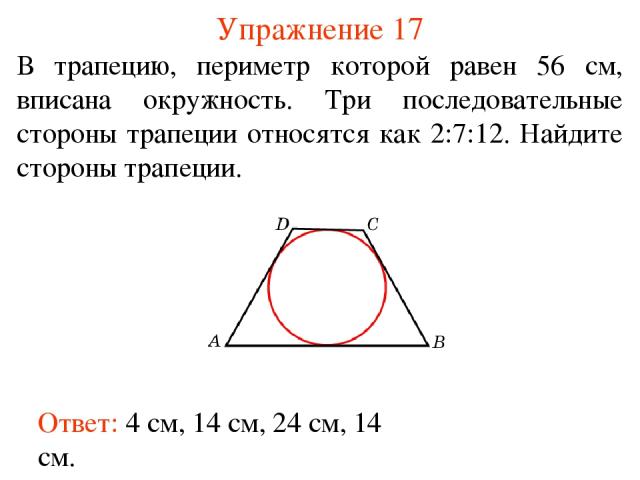
Упражнение 17 В трапецию, периметр которой равен 56 см, вписана окружность. Три последовательные стороны трапеции относятся как 2:7:12. Найдите стороны трапеции. Ответ: 4 см, 14 см, 24 см, 14 см.

Упражнение 18 Боковые стороны трапеции, описанной около окружности, равны 2 см и 4 см. Найдите среднюю линию трапеции. Ответ: 3 см.

Упражнение 19 Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности. Ответ: 2.

Упражнение 20 Докажите, что если в трапецию ABCD (AB||CD) вписана окружность с центром O, то углы AOD и BOC равны 90о. Доказательство. Лучи AO и DO являются биссектрисами внутренних односторонних углов при параллельных прямых AB и CD. Следовательно, угол AOD равен 90о. Аналогично, угол BOC равен 90о.

Упражнение 21 Докажите, что если в равнобедренную трапецию ABCD (AB||CD) вписана окружность, ее боковые стороны AD и BC равны средней линии EF. Доказательство. Сумма боковых сторон трапеции равна сумме оснований. Следовательно, боковая сторона равна полусумме оснований, т.е. равна средней линии.

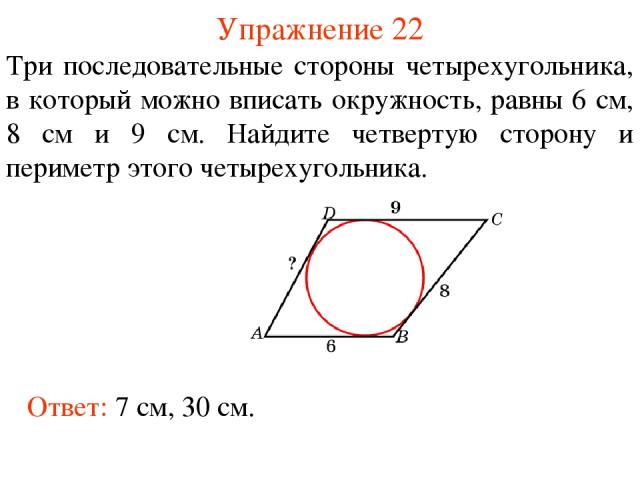
Упражнение 22 Три последовательные стороны четырехугольника, в который можно вписать окружность, равны 6 см, 8 см и 9 см. Найдите четвертую сторону и периметр этого четырехугольника. Ответ: 7 см, 30 см.

Упражнение 23 Противоположные стороны четырехугольника, описанного около окружности, равны 7 см и 10 см. Можно ли по этим данным найти периметр четырехугольника? Ответ: Да, 34 см.

Упражнение 24 Периметр четырехугольника, описанного около окружности, равен 24, две его стороны равны 5 и 6. Найдите большую из оставшихся сторон. Ответ: 7.

Упражнение 25 К окружности, вписанной в треугольник АВС, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника. Ответ: 24.

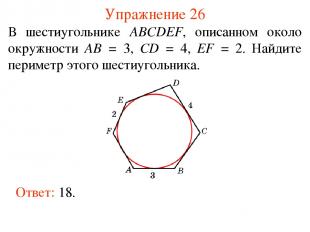
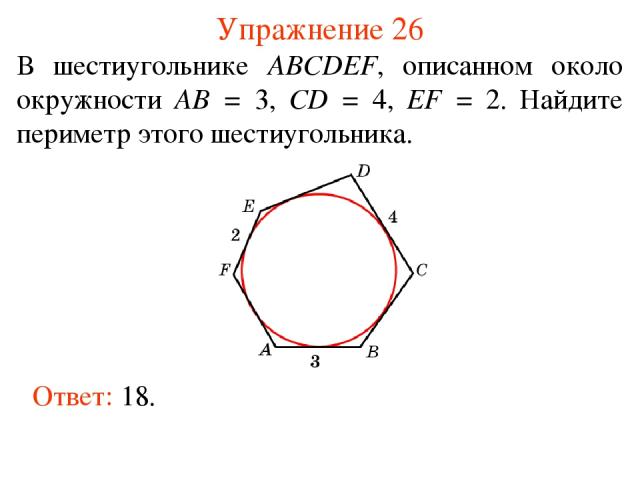
Упражнение 26 В шестиугольнике ABCDEF, описанном около окружности AB = 3, CD = 4, EF = 2. Найдите периметр этого шестиугольника.  Ответ: 18.